[an error occurred while processing this directive] [an error occurred while processing this directive] [an error occurred while processing this directive]
[an error occurred while processing this directive]

植物生态学报 >

2025 , Vol. 49 >Issue 2: 356 - 366

DOI: https://doi.org/10.17521/cjpe.2024.0042

研究论文

幼龄楸树生物量分配规律与异速生长模型

  • 陈文义 ,
  • 王智勇 ,
  • 周梦岩 ,
  • 麻文俊 ,
  • 王军辉 ,
  • 罗志斌 ,
  • 周婧
展开
  • 1林木遗传育种国家重点实验室, 国家林业和草原局森林培育重点实验室, 中国林业科学研究院林业研究所, 北京 100091
    2西北农林科技大学林学院, 陕西杨凌 712100
    3中国林业科学研究院黄河三角洲综合试验中心, 山东东营 257000
    4国家林业和草原局盐碱地研究中心, 中国林业科学研究院生态保护与修复研究所, 北京 100091
*周婧: (gaha2008@126.com)

收稿日期: 2024-02-07

  录用日期: 2024-08-23

  网络出版日期: 2024-08-26

基金资助

国家重点研发计划(2021YFD2200301-4)

收起

Biomass allocation and allometric growth model of young Catalpa bungei

  • CHEN Wen-Yi ,
  • WANG Zhi-Yong ,
  • ZHOU Meng-Yan ,
  • MA Wen-Jun ,
  • WANG Jun-Hui ,
  • LUO Zhi-Bin ,
  • ZHOU Jing
Expand
  • 1State Key Laboratory of Tree Genetics and Breeding, Key Laboratory of Silviculture of the National Forestry and Grassland Administration, Research Institute of Forestry, Chinese Academy of Forestry, Beijing 100091, China
    2College of Forestry, Northwest A&F University, Yangling, Shaanxi 712100, China
    3Comprehensive Experimental Center in Yellow River Delta of Chinese Academy of Forestry, Dongying, Shandong 257000, China
    4Research Center of Saline and Alkali Land of National Forestry and Grassland Administration, Institute of Ecological Conservation and Restoration, Chinese Academy of Forestry, Beijing 100091, China

Received date: 2024-02-07

  Accepted date: 2024-08-23

  Online published: 2024-08-26

Supported by

National Key R&D Program of China(2021YFD2200301-4)

Fold

摘要

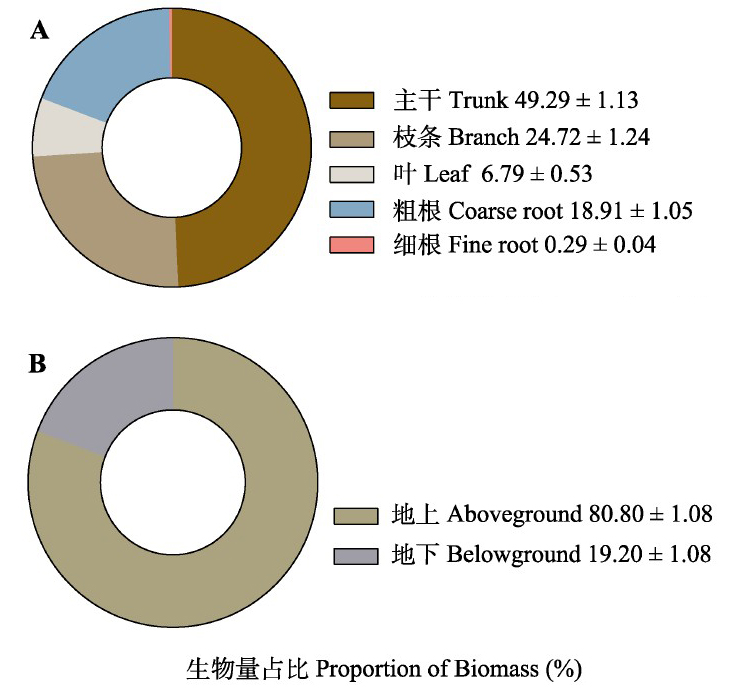
为了探究幼龄楸树(Catalpa bungei)主干、枝条、叶、粗根、细根、整株、地上部分和地下部分各组分生物量分配规律并建立相应的异速生长模型, 在3个相邻省份4个取样点的3-8年幼龄期楸树人工林中, 选取41株胸径(D)范围为3.2-24.8 cm的样木, 采用全称质量法测量楸树各组分生物量并分析其分配规律。分别以D、树高(H)及其复合形式D2H为预测变量, 利用简单幂函数的形式, 构建楸树主干、枝条、叶、粗根、细根、整株、地上部分和地下部分的生物量模型并验证其准确性。幼龄期楸树各组分生物量存在明显异速生长关系。地上部分生物量平均占比为80.54%, 其中主干生物量平均占比为49.29%, 远高于地下部分, 而细根生物量仅占整株的0.29%。在D ≤ 10 cm时, 随D增大, 枝条生物量占比逐渐增大, 而粗根生物量占比减小, 导致地上和地下生物量差距增大; 10 cm < D < 25 cm时, 各组分生物量占比变化放缓。在构建的各组分生物量模型中, 3个预测变量预测精度排序为D > D2H > H, 以D为单一预测变量拟合的主干、枝条、叶、粗根、整株、地上部分和地下部分异速生长模型精度较高, 以D2H为预测变量拟合的细根异速生长模型精度较高; 以不同径级楸树进行抽样, 验证模型准确性的结果显示, 各组分最优预测变量所构建的异速生长模型估测准确度高。幼龄期楸树各组分生物量平均占比顺序为: 主干>枝条>粗根>叶>细根; 随着楸树D增大, 地上部分生物量分配比例呈上升趋势。综合评估异速生长模型的拟合效果可知, D是预测楸树除细根外其他各组分生物量的最可靠变量, D2H是估算细根生物量的可靠变量。利用构建的异速生长模型可预测幼龄楸树的生长规律, 为选育优良楸树无性系提供重要参考。

关键词： 楸树; 生物量分配; 异速生长模型; 生长规律

本文引用格式

陈文义 , 王智勇 , 周梦岩 , 麻文俊 , 王军辉 , 罗志斌 , 周婧 . 幼龄楸树生物量分配规律与异速生长模型[J]. 植物生态学报, 2025 , 49(2) : 356 -366 . DOI: 10.17521/cjpe.2024.0042

Abstract

Aims To explore the biomass allocation of trunk, branch, leaf, coarse root, fine root, total tree, aboveground and belowground of young Catalpa bungei trees, thus to develop corresponding allometric growth models.

Methods Different components of 41 sample trees, with a diameter at breast height (D) ranging from 3.2 to 24.8 cm, were collected from 3 to 8-year-old C. bungei plantation forests at four sampling sites in three neighboring provinces. We utilized the whole mass method to determine the biomass of different components and analyzed their allocation patterns. With D, tree height (H) and their composite form D2H as predictive variables, biomass models for trunk, branch, leaf, coarse root, fine root, total tree, above- and below-ground parts of C. bungei were developed using simple power function. The accuracy of the model was then validated.

Important findings There were obvious allometric growth relationship between the biomass of various components of C. bungei. In average, 80.54% of the total biomass was allocated to above-ground, with an average of 49.29% to the trunks, far exceeding the portion of below-ground biomass, with only 0.29% of the total biomass was allocated to the fine roots. For trees with D≤ 10 cm, the proportion of branch biomass increased, while the coarse root biomass proportion decreased, resulting in a gradual increase in the difference between above- and below-ground biomass with increasing D. Whilst for trees with 10 cm < D< 25 cm, the changes in the proportional biomass of each component diminished. As for allometric models, among the three predictive variables, the accuracy ranking was approximately D > D2H > H. The models using D as a single predictive variable showed highest accuracies for the trunk, branch, leaf, coarse root, total tree, above- and below-ground part biomass, whilst D2H was the best single predictive variable for fine root biomass. Sampling of various diameter classes of C. bungei was used to validate model accuracy, and the results indicated high estimation accuracy of the optimal model for each component. Young C. bungei trees allocated their biomass according to the following order: trunk > branch > coarse root > leaf > fine root. The proportion of above-ground biomass allocation increased as Dincreased. D is the most reliable single variable for predicting the biomass of all components of the C. bungei, except for biomass of the fine roots, which is best predicted by D2H. The optimal allometric growth models constructed can predict the growth rule of young C. bungei accurately, providing significant reference for the selection and breeding of fine C. bungei clones.

Key words： Catalpa bungei; biomass allocation; allometric growth model; growth rule

[an error occurred while processing this directive]

参考文献

[1] Ammer C, Wagner S (2005). An approach for modelling the mean fine-root biomass of Norway spruce stands. Trees, 19, 145-153.
[2] Aneseyee AB, Soromessa T, Elias E, Feyisa GL (2021). Allometric equations for selected Acacia species (Vachellia and Senegalia genera) of Ethiopia. Carbon Balance and Management, 16, 34. DOI: 10.1186/s13021-021-00196-1.
[3] Bowman DMJS, Brienen RJW, Gloor E, Phillips OL, Prior LD (2013). Detecting trends in tree growth: not so simple. Trends in Plant Science, 18, 11-17.
[4] Chang L, Liu K, Wang LG, Yang XL, Sun H (2022). First report of Phytophthora nicotianae causing stem canker of Catalpa bungei (Chinese Catalpa) in China. Plant Disease, 106, 1309. DOI: 10.1094/PDIS-08-21-1778-PDN.
[5] Chen C, Ko SH, Lam TY (2021). Modeling biomass allocation strategy of young planted Zelkova serrata trees in Taiwan with component ratio method and seemingly unrelated regressions. Scientific Reports, 11, 7536. DOI: 10.1038/ s41598-021-87129-7.
[6] Chen JL, Fang X, Wu AC, Xiang WH, Lei PF, Ouyang S (2024). Allometric equations for estimating biomass of natural shrubs and young trees of subtropical forests. New Forests, 55, 15-46.
[7] Chen Q (2015). Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS Journal of Photogrammetry and Remote Sensing, 106, 95-106.
[8] Chen W, Zhang Q, Cihlar J, Bauhus J, Price DT (2004). Estimating fine-root biomass and production of boreal and cool temperate forests using aboveground measurements: a new approach. Plant and Soil, 265, 31-46.
[9] Chen XY, Wang YJ, Li HW, Zhai BQ, Chang J, Wei HM (2021). Preliminary report of demonstration forest test of improved seed of Catalpa bungei. Journal of Henan Forestry Science and Technology, 41(3), 19-21.
  [陈晓燕, 王燕军, 李红伟, 翟宝黔, 常娟, 魏洪敏 (2021). 楸树良种示范林试验初报. 河南林业科技, 41(3), 19-21.]
[10] Chojnacky DC, Heath LS, Jenkins JC (2014). Updated generalized biomass equations for North American tree species. Forestry, 87, 129-151.
[11] Dong LH, Zhang LJ, Li FR (2015). Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees, 29, 1149-1163.
[12] Dybzinski R, Farrior C, Wolf A, Reich PB, Pacala SW (2011). Evolutionarily stable strategy carbon allocation to foliage, wood, and fine roots in trees competing for light and nitrogen: an analytically tractable, individual-based model and quantitative comparisons to data. The American Naturalist, 177, 153-166.
[13] Guan ZZ, Lin D, Chen D, Guo Y, Lu Y, Han Q, Li N, Su Y, Li J, Wang J, Ma W, Qiu Q, He Q (2022). Soil microbial communities response to different fertilization regimes in young Catalpa bungei plantation. Frontiers in Microbiology, 13, 948875. DOI: 10.3389/fmicb.2022.948875.
[14] Han WX, Fang JY (2008). Review on the mechanism models of allometric scaling laws: 3/4 vs. 2/3 power. Chinese Journal of Plant Ecology, 32, 951-960.
  [韩文轩, 方精云 (2008). 幂指数异速生长机制模型综述. 植物生态学报, 32, 951-960.]
[15] Holland R, Castro G, Chavana-Bryant C, Levy R, Moat J, Robson T, Wilkinson T, Wilkes P, Yang WX, Disney M (2024). Giant sequoia (Sequoiadendron giganteum) in the UK: carbon storage potential and growth rates. Royal Society Open Science, 11, 230603. DOI: 10.1098/rsos.230603.
[16] Hossain M, Saha C, Abdullah SMR, Saha S, Siddique MRH (2016). Allometric biomass, nutrient and carbon stock models for Kandelia candel of the Sundarbans, Bangladesh. Trees, 30, 709-717.
[17] Inagaki Y, Nakanishi A, Tange T (2020). A simple method for leaf and branch biomass estimation in Japanese cedar plantations. Trees, 34, 349-356.
[18] Ishihara MI, Utsugi H, Tanouchi H, Aiba M, Kurokawa H, Onoda Y, Nagano M, Umehara T, Ando M, Miyata R, Hiura T (2015). Efficacy of generic allometric equations for estimating biomass: a test in Japanese natural forests. Ecological Applications, 25, 1433-1446.
[19] Jara MC, Henry M, Réjou-Méchain M, Wayson C, Zapata-Cuartas M, Piotto D, Guier FA, Lombis HC, López EC, Lara RC, Rojas KC, Pasquel JD, Montoya AD, Vega JF, Galo AJ, et al. (2015). Guidelines for documenting and reporting tree allometric equations. Annals of Forest Science, 72, 763-768.
[20] Jucker T, Caspersen J, Chave J, Antin C, Barbier N, Bongers F, Dalponte M, van Ewijk KY, Forrester DI, Haeni M, Higgins SI, Holdaway RJ, Iida Y, Lorimer C, Marshall PL, et al. (2017). Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Global Change Biology, 23, 177-190.
[21] Kachamba DJ, Eid T, Gobakken T (2016). Above- and belowground biomass models for trees in the miombo woodlands of Malawi. Forests, 7, 38. DOI: 10.3390/f7020038.
[22] Kaushal R, Islam S, Tewari S, Tomar JMS, Thapliyal S, Madhu M, Trinh TL, Singh T, Singh A, Durai J (2022). An allometric model-based approach for estimating biomass in seven Indian bamboo species in western Himalayan foothills, India. Scientific Reports, 12, 7527. DOI: 10.1038/s41598-022-11394-3.
[23] Kon?pka B, Murga? V, Pajtík J, ?ebeň V, Barka I (2023). Tree biomass and leaf area allometric relations for Betula pendula Roth based on samplings in the western carpathians. Plants, 12, 1607. DOI: 10.3390/plants12081607.
[24] Li C, Barclay H, Roitberg B, Lalonde R (2020). Forest productivity enhancement and compensatory growth: a review and synthesis. Frontiers in Plant Science, 11, 575211. DOI: 10.3389/fpls.2020.575211.
[25] Li W (2014). Biomass Allocation Patterns and Allometric Models of Larix gmelinii. Master degree dissertation, Northeast Forestry University, Harbin. 2-45.
  [李巍 (2014). 兴安落叶松生物量分配格局和异速生长模型. 硕士学位论文, 东北林业大学, 哈尔滨. 2-45.]
[26] Lin KM, Lyu MK, Jiang MH, Chen YM, Li YQ, Chen GS, Xie JS, Yang YS (2017). Improved allometric equations for estimating biomass of the three Castanopsis carlesii H. forest types in subtropical China. New Forests, 48, 115-135.
[27] Lister AJ, Andersen H, Frescino T, Gatziolis D, Healey S, Heath LS, Liknes GC, McRoberts R, Moisen GG, Nelson M, Riemann R, Schleeweis K, Schroeder TA, Westfall J, Wilson BT (2020). Use of remote sensing data to improve the efficiency of national forest inventories: a case study from the United States national forest inventory. Forests, 11, 1364. DOI: 10.3390/f11121364.
[28] Ma WJ, Yi F, Xiao Y, Yang GJ, Chen FJ, Wang JH (2020). Isolation of leaf mesophyll protoplasts optimized by orthogonal design for transient gene expression in Catalpa bungei. Scientia Horticulturae, 274, 109684. DOI: 10.1016/j.scienta.2020.109684.
[29] Meng SW, Zhou G, Liu WH, Yu J, Zhou H, Liu QJ (2024). Species-specific and generalized allometric equations for improving aboveground biomass estimations of 33 understory woody species in northeastern China forest ecosystems. Canadian Journal of Forest Research, 54, 524-542.
[30] Mensah S, Kaka? RG, Seifert T (2016). Patterns of biomass allocation between foliage and woody structure: the effects of tree size and specific functional traits. Annals of Forest Research, 59, 49-60.
[31] Moussa M, Mahamane L (2018). Allometric models for estimating aboveground biomass and carbon in Faidherbia albida and Prosopis africana under agroforestry parklands in drylands of Niger. Journal of Forestry Research, 29, 1703-1717.
[32] Pan Y, Birdsey RA, Phillips OL, Jackson RB (2013). The structure, distribution, and biomass of the world’s forests. Annual Review of Ecology, Evolution, and Systematics, 44, 593-622.
[33] Paul KI, Roxburgh SH, Chave J, England JR, Zerihun A, Specht A, Lewis T, Bennett LT, Baker TG, Adams MA, Huxtable D, Montagu KD, Falster DS, Feller M, Sochacki S, et al. (2016). Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Global Change Biology, 22, 2106-2124.
[34] Peichl M, Arain MA (2007). Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests. Forest Ecology and Management, 253, 68-80.
[35] Poorter H, Jagodzinski AM, Ruiz-Peinado R, Kuyah S, Luo YJ, Oleksyn J, Usoltsev VA, Buckley TN, Reich PB, Sack L (2015). How does biomass distribution change with size and differ among species? An analysis for 1200 plant species from five continents. New Phytologist, 208, 736-749.
[36] Qiu FY, Xiao FM, Wu YF, He XS (2019). Growth and biomass distribution of the middle-age and young Phoebe bournei. Hubei Foresty Science and Technology, 48(3), 12-15.
  [邱凤英, 肖复明, 伍艳芳, 何小三 (2019). 中幼龄闽楠生长及生物量分配特征研究. 湖北林业科技, 48(3), 12-15.]
[37] Quan JE, Ni RY, Wang YG, Sun JJ, Ma MY, Bi HT (2022). Effects of different growth regulators on the rooting of Catalpa bignonioides softwood cuttings. Life, 12, 1231. DOI: 10.3390/life12081231.
[38] Roxburgh SH, Paul KI, Clifford D, England JR, Raison RJ (2015). Guidelines for constructing allometric models for the prediction of woody biomass: How many individuals to harvest? Ecosphere, 6, 1-27.
[39] Schindler Z, Seifert T, Sheppard JP, Morhart C (2023). Allometric models for above-ground biomass, carbon and nutrient content of wild cherry (Prunus avium L.) trees in agroforestry systems. Annals of Forest Science, 80, 28. DOI: 10.1186/s13595-023-01196-6.
[40] Shahabedini S, Ghahramany L, Pulido F, Khosravi S, Moreno G (2018). Estimating leaf biomass of pollarded lebanon oak in open silvopastoral systems using allometric equations. Trees, 32, 99-108.
[41] Solomon N, Birhane E, Tadesse T, Treydte AC, Meles K (2017). Carbon stocks and sequestration potential of dry forests under community management in Tigray, Ethiopia. Ecological Processes, 6, 20. DOI: 10.1186/s13717-017-0088-2.
[42] Strand AE, Pritchard SG, McCormack ML, Davis MA, Oren R (2008). Irreconcilable differences: fine-root life spans and soil carbon persistence. Science, 319, 456-458.
[43] Sun TT, Ren RH, Xing MM, Duan QX, Zhao L, Yan WW, Fang Y, Zhang SY, Dong H, Wang MR, Heng QM, Chen WY, Xu T, Kou LL, Li KP, et al. (2024). Morphological and physiological plasticity of Catalpa bungei roots under partial root-zone drought as affected by nitrogen forms. New Forests, 55, 383-402.
[44] Tobin B, Black K, Osborne B, Reidy B, Bolger T, Nieuwenhuis M (2006). Assessment of allometric algorithms for estimating leaf biomass, leaf area index and litter fall in different-aged Sitka spruce forests. Forestry, 79, 453-465.
[45] Wang CK (2006). Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. Forest Ecology and Management, 222, 9-16.
[46] Wang JC, Qin XM, Xu SQ, Zhao MY, Shu PQ, Xu FJ, Ma JY, Sun Y, Dong H, Guo ZY, Long DP, Ma WJ, Lu YZ, Xie XM, Chen YL, Chu J, Wang JH, Zhang Y (2021). Nitrogen availability affects stem development and response to differential root-zone drought stress in Catalpa bungei. Environmental and Experimental Botany, 186, 104429. DOI: 10.1016/j.envexpbot.2021.104429.
[47] Xiang WH, Liu SH, Deng XW, Shen AH, Lei XD, Tian DL, Zhao MF, Peng CH (2011). General allometric equations and biomass allocation of Pinus massoniana trees on a regional scale in southern China. Ecological Research, 26, 697-711.
[48] Xiao Y, Ma WJ, Lu N, Wang Z, Wang N, Zhai WJ, Kong LS, Qu GZ, Wang QX, Wang JH (2019). Genetic variation of growth traits and genotype-by-environment interactions in clones of Catalpa bungei and Catalpa fargesii f. duclouxii. Forests, 10, 57. DOI: 10.3390/f10010057.
[49] Xiao Y, Wang JH, Yun HL, Yang GJ, Ma JW, Ma WJ, Qu GZ (2021). Genetic evaluation and combined selection for the simultaneous improvement of growth and wood properties in Catalpa bungei clones. Forests, 12, 868. DOI: 10.3390/f12070868.
[50] Xie L, Fu L, Widagdo FRA, Dong L, Li F (2022). Improving the accuracy of tree biomass estimations for three coniferous tree species in Northeast China. Trees, 36, 451-469.
[51] Zeng WS, Chen XY, Yang XY (2021). Developing national and regional individual tree biomass models and analyzing impact of climatic factors on biomass estimation for poplar plantations in China. Trees, 35, 93-102.
[52] Zhao HB, Zhou GY, Li ZJ, Qiu ZJ, Wu ZM, Wang X (2022). Biomass allocation and allometric growth models of four common tree species in southern subtropical evergreen broad-leaved forest. Scientia Silvae Sinicae, 58(2), 23-31.
  [赵厚本, 周光益, 李兆佳, 邱治军, 吴仲民, 王旭 (2022). 南亚热带常绿阔叶林4个常见树种的生物量分配特征与异速生长模型. 林业科学, 58(2), 23-31.]
[53] Zhao JN (2020). Growth Regularity and Cultivation Technology of Catalpa bungei Plantation. Master degree dissertation, South China Agricultural University, Guangzhou.
  [赵江宁 (2020). 楸树人工林生长规律与关键培育技术研究. 硕士学位论文, 华南农业大学, 广州.]
[54] Zheng CH, Mason EG, Jia LM, Wei SP, Sun CW, Duan J (2015). A single-tree additive biomass model of Quercus variabilis Blume forests in North China. Trees, 29, 705-716.
Options
文章导航

/

〈 〉

[an error occurred while processing this directive]