最近邻体分析 (Nearest neighbor analysis, NAA) 属于无样方法之一, 它最早由Clark和Evans (1954) 提出, 其基本理论是通过比较样地内种群的实际分布与假设的随机分布之间的差异, 借以作出种群空间分布类型的判断。它是分析种群空间分布格局的主要方法之一 (Moeur, 1993), 在生态学上得到了广泛的应用 (Füldner,1995;王峥峰等, 1998;Kint et al.2000;戴小华和余世孝, 2003) 。由于直接应用该分析方法会产生边缘效应, 所以一些针对该方法的改进工作也主要集中在边缘效应的修正 (Donnelly, 1978;Füldner,1995) 方面。戴小华和余世孝 (2003) 借 助地理信息系统软件的功能支持, 采用Füldner (1995) 边缘修正后的最近邻体公式, 对规则样地和不规则样地中的种群分布格局进行了研究, 结果表明用最近邻体法分析这两种类型的样地内种群分布格局都非常有效。但该方法只能分析特定尺度下的格局特征, 因此一直被归入单尺度格局分析方法这一类中 (Perry et al.2002) 。
种群分布格局类型的确定与空间尺度相关 (Greig_Smith, 1983;Stewart & Rose, 1990;张金屯, 1998), 一个种在小尺度下可能呈现聚集分布, 而在大尺度下有可能为随机分布或均匀分布, 即种群空间分布格局存在着尺度依赖性。但最近邻体分析只能检验个体分布的随机性, 不能确定种群分布格局随尺度而变化的情况 (Richards & Williamson, 1975;徐化成等, 1994;王峥峰等, 1998) 。因此, 本文提出扩展最近邻体分析法, 并结合实例研究了广东省黑石顶森林群落中5个树木种群的多尺度分布格局特征, 旨在探讨如何改进传统单尺度分析方法以进行多尺度格局分析的途径, 为研究格局与尺度的关系提供新的思路。
1 最近邻体分析的基本理论
式中:CE为Clark_Evans指数, N为样地内个体总数, A为样地面积 (m2), P为样地周长 (m), ri为第i个个体与其最近邻体间的距离 (m) 。
式中:σ为标准差, ρ=N/A为样地内个体密度。
2 扩展最近邻体分析
扩展最近邻体分析 (Extended nearest neighbor analysis, ENNA) 是在传统最近邻体分析方法的基础上, 增加一个距离尺度参数d (m), 并使Clark_Evans指数CE成为它的函数, 即CE (d) = f (d) 。这样, 随距离尺度d的改变就可得到不同的CE (d) 指数值, 从而实现种群多尺度分布格局的检验。
由公式 (1) 可得计算CE所需的全部条件为A、N、P和ri等4个变量, 其中具有决定意义的条件参数为样地面积A。因为对矩形或方形这类特定形状的样地而言, 若其面积A为已知, 则其周长P、样地内的总个体数N和第i个个体与其最近邻体间的距离ri均可由计算机程序间接获得, 比如通过ArcView GIS软件的最近邻体分析模块获得 (戴小华和余世孝, 2003) 。因此面积参数A实际上暗含了一个检验分布格局的特定距离尺度d, 如矩形样地的边长。使此距离尺度d参数化, 即可借用传统的最近邻体分析法作种群分布格局的多尺度分析。
具体地, 增加一个距离尺度参数d, 由它来控制面积A (m2), 进而控制其它各参数, 即新的条件由d、A、N、P和ri等5个变量组成。据此, 对公式 (1) 进行距离尺度d参数化处理, 有:
相应地, 正态分布检验计算式变为:
公式 (4) 、 (5) 、 (6) 中各参数rdA、rdE、Nd、rdi、Ad、Pd、σd的意义分别为:在距离尺度d (m) 范围内, 样地内各个体与其最近邻体间距离的平均值 (m) 、相同环境中随机状态下距离的平均值 (m) 、样地内个体总数、第i个个体与其最近邻体间的距离 (m) 、样地面积 (m2) 、样地周长 (m) 、标准差。
根据公式 (4), 如果CE (d) 小于1则认为种群为聚集分布, 等于1时为随机分布, 大于1时为均匀分布。最终结果的判断还要通过 (5) 式的显著性检验。利用公式 (4) 还可得到CE (d) 与d的关系图, 用于图示分析依赖于距离尺度d的种群空间分布格局。
3 研究实例
3.1 样地调查与数据预处理
在广东省黑石顶自然保护区内选择样地作扩展最近邻体分析的实例研究。有关黑石顶自然保护区概况描述及其植被分类方案参见文献 (余世孝等, 2000) 。
在保护区石门塘西北的架桥坑 (地理坐标为23°26′ N, 111°53′ E) 设置一块面积为64 m×64 m的样地, 对样地内胸径1 cm以上的乔灌木物种进行每木调查, 调查内容包括种名、胸径、高度、冠幅和个体在样地中的坐标位置。该群落为黑石顶自然保护区分布最广的混交林类型—以马尾松为优势的针阔叶混交林, 马尾松属衰退种群, 其在群落中的地位与阔叶树相近, 其林相与阔叶林很相似 (余世孝等,2000) 。
3.2 点分布图
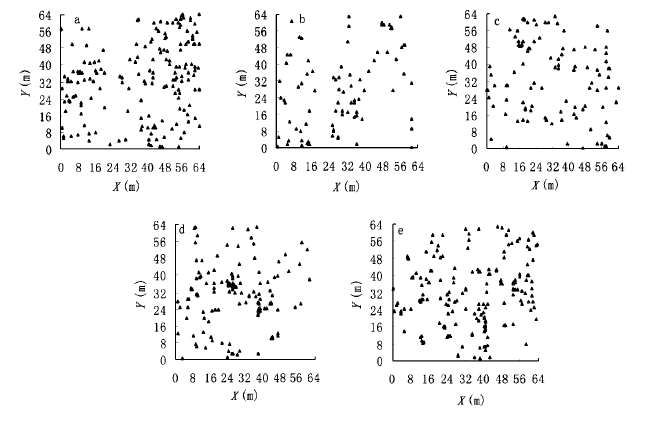
图1
图1
5个树木种群的点分布图
a.马尾松Pinus massoniana b.黄牛奶树Symplocos laurina c.水栗Castanopsis nigrescens d.鼠刺Itea chinensis e.桃金娘Rhodomyrtus tomentosa
Fig.1
Mapped points pattern of five tree populations
3.3 最近邻体分析模块
3.4 结果与分析
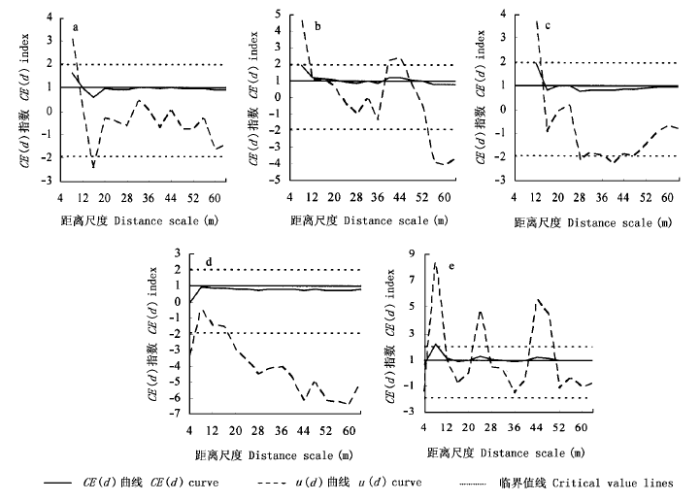
分布格局曲线图以图示化的方式反映CE (d) 指数与距离尺度d之 间的关系, 描述种群分布格局随距离尺度变化而变化的走势。结果表明 (图2), 在黑石顶针阔叶混交林群落中, 马尾松显著表现为随机分布, 鼠刺种群显著表现为聚集分布, 黄牛奶树、水栗、桃金娘等3个种群的分布格局都表现出不同程度的尺度相关性。随距离尺度的增加, 这4个种群的分布格局以聚集或随机分布为主要类型。
图2
图2
5个树木种群的分布格局
a.马尾松Pinus massoniana b.黄牛奶树Symplocos laurina c.水栗Castanopsis nigrescens d.鼠刺Itea chinensis e.桃金娘Rhodomyrtus tomentosa
Fig.2
Spatial pattern of five tree populations
鼠刺 (图2d) 在各个尺度范围内CE (d) 指数值均小于1, 倾向于聚集分布。显著性检验的结果也表明, 该种群在20 m以上尺度范围内均为聚集分布。
4 讨论与结论
4.1 关于5个种群的多尺度分布格局
关于种群空间分布格局的尺度依赖性已有论述 (Greig_Smith, 1983;Stewart & Rose, 1990;张金屯, 1998) 。本研究的结果 (图2) 也表明, 随距离尺度d的改变, 各种群的CE (d) 指数曲线均出现不同程度的波动, 意味着种群分布格局存在尺度依赖性。其可能原因是:1) 种群个体数的变化。尺度的改变意味着研究区域的改变, 因而其内种群个体数也随之改变, 则由公式 (5) 可知, 格局分析的结果必然改变。2) 种群所处生境条件等因素的变化。生态学系统的空间异质性是生物系统的主要属性之一 (李哈滨等, 1998), 而它是尺度的函数, 即其变异依赖于时空尺度 (Li & Reynolds, 1995) 。因此, 处于异质性空间中的种群其分布格局也会表现出相应的变化。3) 种内、种间关系的变化。最近邻体分析方法的一个隐含假设就是, 植物种群的相互作用主要发生在其最邻近的个体之间。当这种作用发生在同种之间时, 即发生自疏现象;发生在异种之间时, 即发生他疏现象。已有研究表明 (侯向阳和韩进轩, 1997), 在时间尺度上, 林木的随机自疏是种群格局动态变化的重要原因。本研究表明, 随空间尺度的改变, 自疏和他疏现象的作用范围也会相应改变, 小尺度上形成的格局会在较大尺度上进行复合, 进而表现为种群格局的尺度变化。
广东省黑石顶自然保护区地处南亚热带, 该区森林群落普遍存在由马尾松林向常绿阔叶林演变的趋势 (周先叶等, 1999;昝启杰等, 2000), 马尾松既是先锋种, 又是消退种 (丁圣彦和宋永昌, 1998) 。图2表明, 在16~64 m较宽的尺度范围内, 马尾松种群均呈随机分布格局, 种群个体的随机死亡可能是其主要原因。因所研究群落为处于森林群落演替中期的针阔叶混交林阶段, 水栗、鼠刺等其它阔叶树种已逐渐占据群落上层, 并将发展为群落中的优势种, 而马尾松种群则处于消退状态。根据丁圣彦和宋永昌 (1998) 的 研究结果, 一方面, 因群落内光照强度过低, 使马尾松种群更新苗处于光补偿点之下, 难以生长;另一方面, 群落内耐荫树种的抑制使马尾松成树的物质合成能力逐渐减弱, 物质分解能力逐渐加强, 以致其在演替过程中逐渐消失。由自疏或他疏引起的随机死亡将导致种群格局由聚集分布向均匀分布偏移 (Antonovics & Levin, 1980;Peterson & Squiers, 1995), 而随机分布则是这种偏移过程的中间状态。
4.2 关于扩展最近邻体方法
以广东省黑石顶自然保护区针阔叶混交林中的马尾松、黄牛奶树、水栗、鼠刺和桃金娘等5个 代表性种群为实例的研究表明, 5个种群均表现出不同程度的尺度相关性。应用本文提出的扩展最近邻体分析方法ENNA能够检测出种群空间分布格局的尺度依赖性, 获得关于种群空间分布格局的多尺度信息, 其分析结果具有明显的生态学意义, 因而, 该方法是进行种群多尺度空间格局分析的有效方法。进一步还可采用本文的扩展思路对其它隐含距离信息的传统分析方法作类似的改进, 使之获得多尺度分析功能, 以进行生态学问题的多尺度研究。因而, 本文研究的思路还具有一定的方法论意义。
在地理信息系统软件ArcView的支持下, 扩展最近邻体分析方法还可用于对多个种群的空间分布格局进行多尺度检验, 其结果可用于发现具有相似分布格局的种组, 即格局种组, 以进行其它相关生态学研究;或寻找相同种群其分布格局存在差异的原因, 如生长阶段的差异、生境异质性等。因此, 扩展最近邻体分析方法具有较好的生态学应用前景。
参考文献
Theecologicaland geneticconsequencesofdensity_dependentregulationinplants
Spatialhetero geneityinecologicalsystems
Distancetonearestneighbourasameasureofspatialrelationshipsinpopulations
Analysisofpop ulationdistributionpatternbasedonGIStechnique
DecliningcausesofPinusmassonianaintheprocessofsuccessionofev ergreenbroad_leavedforest
FractalTheoryandItsApplica tions
Simulationstodeterminethevarianceandedgeeffectoftotalnearest-neighbourdistance.In:Hod derIed
SpatialpatternanalysisinecologybasedonRipley'sK_function:introductionandmethodsofedgecor rection
SimulationanalysisofspatialpatternsofmainspeciesintheKorean-pinebroadleavedforestinChangbaiMountain
本文引入依坐标点集的空间格局模拟分析法研究了长白山红松林主要树种的格局分布,以及红松不同年龄级格局分布的动态。结果表明:红松在不同的林型、不同的生长发育阶段表现不同的空间格局,乔木层红松属随机型分布,在红松云冷杉林中非随机性较强;随着年龄级增长,红松的空间格局从聚集向随机发展,林木的随机自稀是种群格局动态变化的重要原因。
Quantifi cationofforeststandstructureappliedtoScotspine (PinussylvestrisL.)forests
.In:MasonBed.SilvicultureandBiodiversityofScotsPineForestsinEurope.
Ondefinitionandquantificationofheterogeneity
Theoryandmethodologyofspatialheterogeneityquantification
Ecologicalscaleandscaling
Fractalproper tiesofvegetationpatterns
目前植被格局研究存在一些问题,分形模型是解决这些问题的有力工具。选择从分枝到景观的各个等级层次上若干有代表性的研究实例进行介绍,给出了尺度、自相似性和分形维数在植被格局研究中的应用方法,说明了分形模型描述植被格局的实用性和优越性。在此基础上提出植被格局的分形机制,认为植被格局是具有自组织特征的分形体。最后对植被格局的分形模型进行了评价,提出研究中需要注意的若干问题以及未来的发展方向。
Characterizingspatialpatternsoftreesusingstem_mappeddata
Illustrationsandguidelinesforselectingstatisticalmethodsforquantifyingspa tialpatterninecologicaldata
Anunexpectedchangeinspatialpatternacross10 yearsinanaspen-white-pineforest
Treefallsandpatternsofunderstoryspeciesinawetlowlandtropicalforest
Thesignificanceoflifehistorystrategiesinthedevelopmentalhistoryofmixedbeechforests, NewZewland
EdgecorrectionofRipley'sK (d) functiononpopulationspatialpatternanalysis
Distributionpat ternoftreepopulationsintropicalforestandcomparisonofitsstudymethods
Spatialecologyandlandscapeheterogeneity
AstudyinspatialpatternsoftreesinvirginLarixgmeliniforest
ThevegetationclassificationanditsdigitizedmapofHeishidingNatureReserve, GuangdongI
.Thedistributionofthevegetationtypeandformation.
Dynamicsofcommunitystruc tureinsuccessionalprocessofneedleandbroad_leavedmixedforestinHeishidingofGuangdong
Analysisofspatialpointpatternforplantspecies
植物种群在群落中的分布格局与空间尺度有着密切关系,传统的样方取样及其格局分析方法,只能分析一种尺度下的格局。本文引入一种新的格局分析方法——点格局分析,其是以种群空间分布的坐标点图为基础,通过本文对美国密西根州克林顿县栎林3个优势种格局分析,它有3个明显的优点:1)能够分析各种尺度下的种群格局和种间关系,结果清楚,直观;2)所描述的结果更符合实际,尤其是对群落结构的描述;3)它有利于定点观察,研究时间与种群格局的关系,本文分析的3个种集群特征明显,但随尺度的变化有不同的分布趋势,3个种间的关系也是如此。
ThecommunitydynamicsoftheforestsecondarysuccessioninHeishidingNaturalReserveofGuangdongprovince