蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 )。随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 )。作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 )。
三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 )。它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果。
三温模型反演与分离蒸散发组分(蒸发与蒸腾)的关键包括: 1)蒸发、蒸腾系数物理取值的合理范围(边界)的确定; 2)植被与土壤组分温度的确定; 3)参考土壤与参考植被温度的确定。目前研究已明确三温模型中植被蒸腾扩散系数、土壤蒸发扩散系数的边界(Qiu et al ., 2003 , 2006 ), 植被与土壤组分温度的确定也有较为成熟的方法(Lhomme et al ., 1994 ), 而参考温度的参数化过程一直是三温模型反演土壤蒸发和植被蒸腾面临的难点。三温模型应用于估算空间异质性更强、微气候环境更加复杂的城市绿地蒸腾时, 参考温度参数化对三温模型应用于城市复杂下垫面环境典型绿地蒸腾估算的精度及适用性的影响如何? 这一关键科学问题亟待研究。
目前三温模型反演植被蒸腾中参考温度参数化的方法主要有3种: 1)实测法, 即以干燥的绿色树叶、纸片等为参考叶片, 通过热红外温度传感器或者热红外成像仪直接观测(Qiu, 1996 ), 但参考叶片温度的不同取值方法使其具有不确定性; 2)植被与土壤组分温度最值法, 如根据卫星或地面热红外遥感测算的植被与土壤组分温度, 取植被像元温度的最大值作为参考植被温度(Xiong & Qiu, 2014 ), 此时温度最大值的确定受温度图像代表范围, 以及组分温度分离精度等影响; 3)地表温度最值法, 即直接以热红外地表温度(不区分组分温度)最大值为参考温度(Qiu et al ., 1998 ), 在干旱、半干旱区通常对应干燥土壤, 但在湿润区有待检验。基于以上研究现状, 当三温模型推广应用时, 需要深入细致地研究其各输入变量尤其是参考温度的参数化过程。
为此, 本研究以北京大学深圳研究生院校园为研究区, 依托研究区域草坪的波文比观测, 以期1)对三温模型植被蒸腾子模型中涉及的参数做敏感性分析, 确定影响蒸腾估算精度的关键参数; 2)研究不同参考温度取值对三温模型计算植被蒸腾精度的影响; 3)确定三温模型参考温度这一关键参数最佳值的选取, 对三温模型加以改进, 提高其测算精度。
1 材料和方法
1.1 研究区域
深圳市地处东南沿海, 位于北回归线以南, 为亚热带海洋性气候, 年平均气温22.3 ℃, 平均日辐射达5.6 h; 年降水量1 936 mm, 降水较多集中在湿季(4-9月), 而干季(10-3月)降水较少。本研究的观测实验在北京大学深圳研究生院校园(深圳市南山区西丽深圳大学城)内(图1A )展开, 在园区D栋和E栋建筑之间的沟叶结缕草(Zoysia matrella )草坪中央架设了一套波文比观测系统(图1B )。热红外拍摄在上述草坪同步进行。
图1
图1
研究区概况。A, 北京大学深圳研究生院校园。B, 波文比系统。
Fig. 1
Study area. A, Peking University Shenzhen Graduate School campus. B, Bowen ratio system.
1.2 波文比观测
波文比观测系统经过检测和调试, 于2014年7月10日起正常运行。观测的基础气象数据包括太阳辐射、光合有效辐射、净辐射、土壤热通量(2个重复)、高度1.5和2.0 m的温度和湿度, 传感器具体信息如表1 所示。各项数据利用CR1000数据采集器(Campbell, Logan, USA)进行自动记录, 每1 min测读1次, 波文比系统每10 min进行数值平均并储存。
1.3 热红外遥感拍摄
草坪表面温度通过红外热像仪获取, 其测量精度<2%。实验期间将参考叶片置于观测植被附近, 使参考叶片与植被处在相同的热环境中, 参考叶片与植被同步拍摄。参考叶片可用A3大小绿色硬纸片, 选择时纸片颜色要尽量接近植被真实叶片颜色, 保持纸面平整光滑不弯曲, 表面粗糙或折痕会改变太阳光的传播路径从而影响观测准确度。
在2018年5月30、31日, 6月1、2日, 8月1、5、9日, 10月3、19日和11月17日, 包含湿季和干季的10个典型晴天或阴天作为观测日, 在地面无明显积水的白天开展实验。热红外观测在实验日的8:00-18:00进行, 每隔1 h观测一次, 每次拍摄3张。2018年5月30日13:00拍摄的草坪和参考叶片可见光与热红外图像如图2 所示。
图2
图2
草坪和参考叶片的可见光与热红外图像。A, 草坪可见光图像。B, 草坪热红外图像。C, 参考叶片可见光图像。D, 参考叶片热红外图像。
Fig. 2
Visible light and thermal infrared images of the lawn and the reference leaf. A, Visible images of the lawn. B, Thermal infrared images of the lawn. C, Visible images of the reference leaf. D, Thermal infrared images of the reference leaf.
1.4 波文比能量平衡法
波文比-能量平衡法(Bowen ratio energy balance)是Bowen在1926 年提出的蒸散发计算方法。其原理是根据能量守恒定律, 植被冠层接收的太阳辐射能量等于各途径支出的能量总和, 能量平衡方程为:
(1) ${{\text{R}}_{\text{n}}}\text{= LE + H + G}$
式中, Rn 为太阳净辐射(W∙m-2 ); G为土壤热通量(W∙m-2 ); H为显热通量(W∙m-2 ); LE为潜热通量(W∙m-2 )。Rn 、G由波文比观测系统直接测得, 潜热通量LE和显热通量H由计算得出。
在某一界面上, 显热通量与潜热通量的比值被定义为波文比(β ), β 可以表示为垂直方向上温度梯度和湿度梯度的函数。假定乱流水汽湍流交换系数(K w )和乱流热交换系数(K h )相等(Dyer, 1974 ), β 可以定义为:
(2) $\beta =\frac{\text{H}}{\text{LE}}=\frac{{{\rho }_{\text{a}}}{{C}_{\text{p}}}{{K}_{\text{h}}}\frac{\partial T}{\partial z}}{\varepsilon \text{L/}P{{\rho }_{\text{a}}}{{K}_{\text{w}}}\frac{\partial e}{\partial z}}=\frac{{{C}_{\text{p}}}P}{\varepsilon \text{L}}\times \frac{\frac{\partial T}{\partial z}}{\frac{\partial e}{\partial z}}=\gamma \frac{\Delta T}{\Delta e}$
(3) $\gamma =\frac{{{C}_{\text{p}}}P}{\varepsilon \text{L}}$
(4) $\text{L}=1000\times \left( 2500.78-2.36\times \frac{({{T}_{1}}+{{T}_{2}})}{2} \right)$
(5) $\text{ }\Delta T={{T}_{1}}-{{T}_{2}}$
(6) ${{e}_{1}}=0.6108{{\text{e}}^{\frac{17.27{{T}_{1}}}{{{T}_{1}}+237.3}}}\times \frac{{{q}_{1}}}{100}$
(7) ${{e}_{2}}=0.6108{{\text{e}}^{\frac{17.27{{T}_{2}}}{{{T}_{2}}+237.3}}}\times \frac{{{q}_{2}}}{100}$
(8) $\text{ }\Delta e={{e}_{1}}-{{e}_{2}}$
式中, ρ a 为空气密度(kg∙m-3 ); C p 为空气定压比热(估计为1.013 kJ∙kg-1 ∙℃-1 ); ε 为水汽和干燥空气的分子量之比, 为常数0.622; γ 为干湿表常数(kPa∙℃-1 ); P 为大气压(根据深圳海拔估计为101 kPa); L为汽化潜热(J·kg-1 ); 本研究中仪器安装在1.5与2.0 m处测定空气相关值, T 1 为1.5 m高度处的气温, T 2 为2.0 m高度处的气温, $\frac{\partial T}{\partial z}$ ( ΔT )为上下两个高度的气温差(℃); e 1 为1.5 m高度处空气的水汽压, e 2 为2.0 m高度处空气的水汽压, q 1 为1.5 m高度处空气的湿度(%), q 2 为2.0 m高度处空气的湿度(%), $\frac{\partial T}{\partial z}$ ( Δe )为上下两个高度空气的水汽压差(kPa)。联立公式(1)和公式(2), 可以计算得到LE、H以及蒸散发量(E, 通常表示为ET)的公式为:
(9) $\text{LE}=\frac{{{\text{R}}_{\text{n}}}-\text{G}}{1+\beta }$
(10) $\text{H}=\frac{\beta ({{\text{R}}_{\text{n}}}-\text{G})}{1+\beta }$
(11) $\text{ET}=\frac{\text{LE}}{\text{L}}=\frac{{{\text{R}}_{\text{n}}}-\text{G}}{\text{L}(1+\beta )}$
1.5 三温模型+热红外遥感法
邱国玉提出的三温模型(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 )是一种测算蒸散发和评估环境质量的方法, 因为该模型的核心参数是表面温度、参考表面温度和气温, 故被称为三温模型。本研究仅用到植被蒸腾模型。
当地表被植被覆盖时, 可以忽略土壤热通量, 简化地表能量平衡方程, 植被表面的能量平衡可表示为:
(12) $\text{L}{{\text{E}}_{\text{c}}}\text{= }{{\text{R}}_{\text{n,c}}}-{{\text{H}}_{\text{c}}}$
式中, LEc 为植被潜热通量, Rn,c 为植被表面净辐射, Hc 为植被表面显热通量, 各参数单位与公式(1)中一致。公式(2)经过参数替换后, Hc 可表示为(Monteith & Unsworth, 2013 ):
(13) ${{\text{H}}_{\text{c}}}=\frac{{{\rho }_{\text{a}}}{{C}_{\text{p}}}({{T}_{\text{c}}}-{{T}_{\text{a}}})}{{{r}_{\text{a}}}}$
式中, ρ a 表示空气密度(kg∙m-3 ), 为1.29 kg∙m-3 , C p 为空气定压比热(kJ∙kg-1 ∙℃-1 ), T c 为植被表面温度(℃), T a 为气温(℃), r a 为空气动力学阻抗(s∙m-1 )。下标c代表植被。参考叶片是无水分蒸腾的模拟叶片, 即LEcp 为0 W∙m-2 , 蒸腾量为0, 假设参考叶片不会对周边的大气条件产生显著影响, 地表植被与参考叶片的r a 近似相等, 根据公式(12)和公式(13), r a 可以表示为:
(14) ${{r}_{\text{a}}}=\frac{{{\rho }_{\text{a}}}{{C}_{\text{p}}}({{T}_{\text{cp}}}-{{T}_{\text{a}}})}{{{\text{R}}_{\text{n,cp}}}}$
式中, T cp 为参考叶片温度, Rn,cp 为参考叶片净辐射。参数下标cp代表参考叶片。将各参数表达式代入公式(12), 得到三温模型植被蒸腾表达式:
(15) $\text{L}{{\text{E}}_{\text{c}}}={{\text{R}}_{\text{n,c}}}-{{\text{R}}_{\text{n,cp}}}\times \frac{{{T}_{\text{c}}}-{{T}_{\text{a}}}}{{{T}_{\text{cp}}}-{{T}_{\text{a}}}}$
式中, Rn,c 和T a 可以直接通过波文比系统获取; T c 可以通过解译草坪的热红外图像获取; T cp 从作为参考叶片的纸片的温度上取值; 参考叶片净辐射(Rn,cp , W∙m-2 )可由以下公式(Jensen et al ., 1990 )计算:
(16) ${{\text{R}}_{\text{n,cp}}}=(1-\alpha )\times {{\text{R}}_{\text{s,cp}}}+\Delta {{\text{R}}_{\text{l,cp}}}$
式中, α 为参考叶片反照率, 取值0.22; Rs,cp 为参考叶片上短波太阳辐射(W∙m-2 ), 可以通过波文比系统直接观测; ΔR1,cp 为参考叶片上净长波辐射(W∙m-2 ), 由下述公式(Weiss, 1982 ; Burman et al ., 1983 )计算得出:
(17) $\begin{matrix} & \Delta {{\text{R}}_{\text{l,cp}}}=(0.4+0.6{{\text{R}}_{\text{s}}}\text{/}{{\text{R}}_{\text{ss}}})\times \\ & \ \ \ \ \ \ \ \ \ \ \ \ ({{\varepsilon }_{\text{a}}}{{\varepsilon }_{\text{cp}}}\sigma T_{\text{a}}^{4}-{{\varepsilon }_{\text{cp}}}\sigma T_{\text{cp}}^{4}) \\ \end{matrix}$
式中, Rss 为晴天的太阳辐射(W∙m-2 ), ε cp 为参考叶片表面反射率, 本研究取值0.98, σ 表示Stefan-Boltzman常数(5.675 × 10-8 J∙m-2 ∙K-4 ∙s-1 )。观测当天为晴天, Rs ≈ Rss , 那么0.4 + 0.6 Rs /Rss ≈ 1。ε a 为大气发射率, 可表示为(Hatfield et al ., 1983 ): εa = 0.92 × 10 -5 T a 2 。
1.6 三温模型敏感性分析方法
为了解输入参数对三温模型计算结果的影响程度, 对三温模型做敏感性分析, 对于提高三温模型计算准确性十分必要。本研究采用Beven (1979 )提出的敏感性分析方法, 具体如下:
(18) $\text{LE}=f({{p}_{1}},{{p}_{2}},{{p}_{3}},\cdots,{{p}_{n}})$
式中有n 个输入变量pi , 由pi 的变化或者不确定性引起的LE的变化可表示为:
(19) $\begin{matrix} & \text{LE}+\Delta \text{LE}=f({{p}_{1}}+\Delta {{p}_{1}},{{p}_{2}}+\Delta {{p}_{2}}, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{p}_{3}}+\Delta {{p}_{3}},\cdots,{{p}_{n}}+\Delta {{p}_{n}}) \\ \end{matrix}$
展开(19)式的泰勒级数, 忽略二阶及以上的项, 得出:
(20) $\begin{matrix} & \Delta \text{LE}=\frac{\partial \text{LE}}{\partial {{p}_{1}}}\Delta {{p}_{1}}+\frac{\partial \text{LE}}{\partial {{p}_{2}}}\Delta {{p}_{2}}+ \\ & \ \ \ \ \ \ \ \ \ \frac{\partial \text{LE}}{\partial {{p}_{3}}}\Delta {{p}_{3}}+\cdots +\frac{\partial \text{LE}}{\partial {{p}_{n}}}\Delta {{p}_{n}} \\ \end{matrix}$
式中, 差分$\partial (\text{LE})\text{/}\partial {{p}_{i}}$ ${{S}_{i}}$ ) 定义为(Beven, 1979 ):
(21) ${{S}_{i}}=\frac{\partial \text{LE}}{\partial {{p}_{i}}}\times \frac{{{p}_{i}}}{\text{LE}}$
式中, Si 表示参数pi 的变化引起LE的变化, 例如Si 为0.1时, 表明参数pi 增加10%时预期LE可能增加1%。系数为负表示pi 的增加会导致LE降低。公式(21)对LE和pi 的大小敏感, 特别是如果LE或pi 各自趋向于零, 或者pi 取值的范围与其大小相比很小, 则Si 可能不能很好地指示pi 对LE影响的显著性(Beven, 1979 )。
本研究中三温模型植被蒸腾子模型每个输入参数的敏感性系数如下:
(22) $S({{\text{R}}_{\text{n,c}}})=\frac{{{\text{R}}_{\text{n,c}}}}{\text{LE}}$
(23) $S({{\text{R}}_{\text{n,cp}}})=\frac{{{T}_{\text{c}}}-{{T}_{\text{a}}}}{{{T}_{\text{a}}}-{{T}_{\text{cp}}}}\times \frac{{{\text{R}}_{\text{n,cp}}}}{\text{LE}}$
(24) $S({{T}_{\text{c}}})=\frac{{{\text{R}}_{\text{n,cp}}}}{{{T}_{\text{a}}}-{{T}_{\text{cp}}}}\times \frac{{{T}_{\text{c}}}}{\text{LE}}$
(25) $S({{T}_{\text{a}}})=\left[ \frac{{{\text{R}}_{\text{n,cp}}}}{{{T}_{\text{cp}}}-{{T}_{\text{a}}}}-\frac{{{\text{R}}_{\text{n,cp}}}({{T}_{\text{c}}}-{{T}_{\text{a}}})}{{{({{T}_{\text{cp}}}-{{T}_{\text{a}}})}^{2}}} \right]\times \frac{{{T}_{\text{a}}}}{\text{LE}}$
(26) $S({{T}_{\text{cp}}})=\frac{{{\text{R}}_{\text{n,cp}}}({{T}_{\text{c}}}-{{T}_{\text{a}}})}{{{({{T}_{\text{a}}}-{{T}_{\text{cp}}})}^{2}}}\times \frac{{{T}_{\text{cp}}}}{\text{LE}}$
1.7 不同参考温度取值对三温模型反演植被蒸腾精度影响的研究方法
参考叶片温度的取值方法主要包括: 1)设置干燥、颜色相近的绿纸片为参考叶片, 解译其热红外图像为参考叶片温度; 2)近似取植被表面温度的最大值为参考叶片温度。为了对比以上取值方法的合理性, 本研究首先分别取每小时整点热红外遥感拍摄测得的参考叶片温度最大值、前10%平均值、前20%平均值、前50%平均值和平均值为参考叶片温度, 代入三温模型计算草坪蒸腾量, 与依据波文比系统在对应每小时整点观测到的数据计算得到的结果进行回归分析后比较, 确定参考叶片最佳温度取值方法; 然后进一步对比了参考叶片最佳温度取值方法与最大植被冠层温度法, 最终确定参考叶片温度的最佳取值。
本研究使用回归评价指标相关系数(R 2 )和均方根误差(RMSE )综合评价计算精度。R 2 的范围在0-1之间, 越接近于1说明相关性越好; RMSE 是预测值与真实值误差平方根的平均值, 其值越小说明精确度越好。通过方差分析来检验选择不同参考叶片温度对反演效果是否有显著影响。
2 结果
2.1 三温模型参数敏感性分析
选择一个典型晴天(2018年5月30日)进行分析, Rn 的日间变化见图3 。T a 和T c 的日间变化见图4 。三温模型的植被蒸腾计算公式中涉及Rn,c 、Rn,cp 、T c 、T cp 和T a 5个输入变量。本研究选择一个典型晴天(2018年5月30日)对三温模型输入变量进行敏感性分析, 其输入参数的敏感性系数在日间随时间的变化如图5 所示。可以看出, Rn 和T cp 这两个输入变量的敏感性系数较大; Rn 和Rn,cp 的敏感性系数整体相对稳定, Rn 的敏感性系数值在0.85-1.42之间, Rn,cp 的敏感性系数值在-0.42-0.13之间。而T a , T c 和T cp 的敏感性系数变化幅度较大, 因此对这3个温度项进行后续误差分析。
图3
图3
净辐射的日间变化。
Fig. 3
Diurnal variation of the net radiation.
图4
图4
气温(Ta )和植被表面温度(Tc )的日间变化。
Fig. 4
Diurnal variation of the air temperature (Ta ) and vegetation canopy temperature (Tc ).
图5
图5
各参数敏感性系数的日间变化。Rn , 净辐射; Rn,cp , 参考叶片净辐射; Ta , 气温; Tc , 植被表面温度; Tcp , 参考叶片温度。
Fig. 5
Diurnal variation of the sensitivity coefficients of each parameter. Rn , net radiation; Rn,cp , reference leaf net radiation; Ta , air temperature; Tc , vegetation canopy temperature; Tcp , reference leaf temperature.
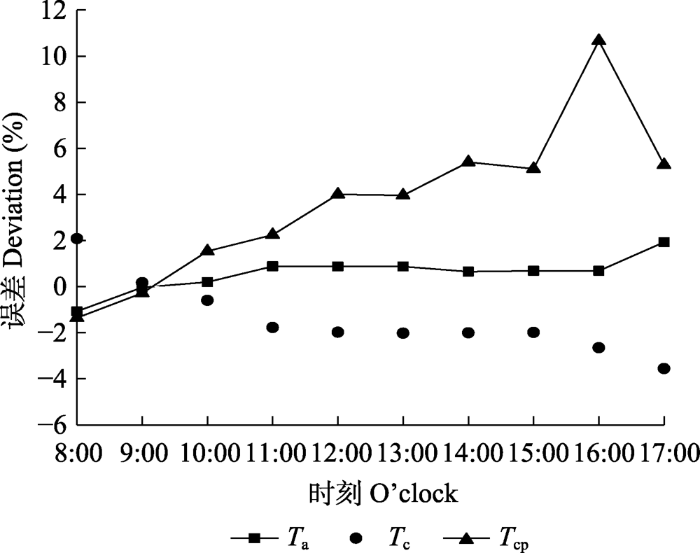
根据上述波文比系统各测量仪器的参数, 气温测量精度<3%, 因此用T a 的敏感性系数乘以3%表示气温测量对计算结果造成的误差; 根据热红外成像仪的参数, T c 测量精度<2%, 用T c 的敏感性系数乘以2%表示T c 对计算结果造成的误差; 而T cp 存在取值偏差, 取值不同会造成计算结果的误差, 用T cp 的敏感性系数乘以其取值范围的百分比系数(具体为(最大值-平均值)/平均值), 即为T cp 对计算结果造成的误差。
上述3个温度参数的误差量化后结果如图6 所示。由图可知, 相较于T a 和T c , 参考叶片温度T cp 取值能够引起更大的结果误差, 这一结果说明参考叶片温度取值对于准确应用三温模型计算植被蒸腾的重要性, 探究参考叶片温度的取值具有重要意义。
图6
图6
气温(Ta )、植被表面温度(Tc )和参考叶片温度(Tcp )对结果造成误差的日变化。
Fig. 6
Diurnal variation of the deviation caused by air temperature (Ta ), vegetation canopy temperature (Tc ) and reference leaf temperature (Tcp ).
2.2 参考叶片温度取值对三温模型估算精度影响
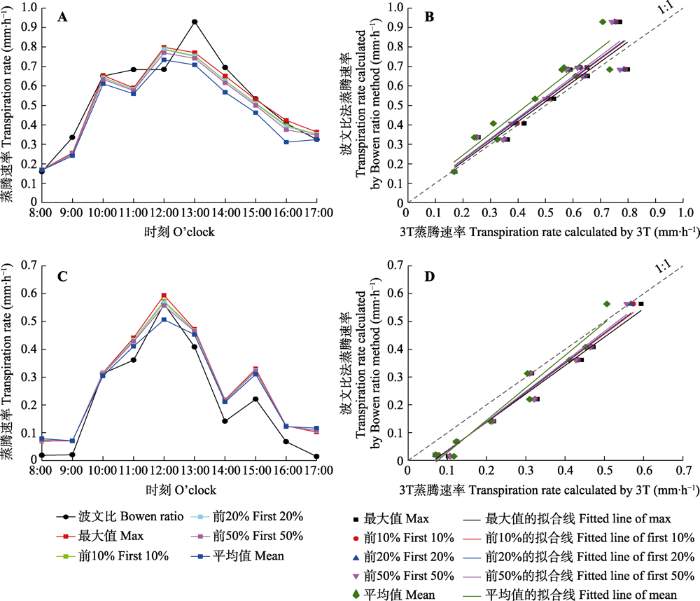
在观测期间, 分别取参考叶片上热红外图像全部温度值的最大值、前10%平均值、前20%平均值、前50%平均值和平均值为参考叶片温度, 代入三温模型计算草坪蒸腾量, 并与波文比观测结果进行对比。其中2018年湿季的5月30日和干季的11月7日蒸腾量估算精度对比情况如图7 所示。可以看出, 使用不同参考叶片温度取值方法计算得到的草坪蒸腾速率与波文比法日内变化规律基本一致, 观测日内草坪蒸腾速率虽有不同程度波动, 但有明显单峰变化曲线。
图7
图7
波文比法与三温模型(3T)不同参考叶片温度取值计算草坪蒸腾速率结果对比。A, B, 2018年5月30日。C, D, 2018年11月7日。
Fig. 7
Comparison of lawn transpiration rate calculated by Bowen ratio method and three-temperature model (3T) with different reference leaf temperature value. A, B, May 30, 2018. C, D, November 7, 2018.
表2 汇总了观测期间不同观测日的三温模型估算结果与波文比观测结果的线性拟合结果。可以看出, 通过设置绿纸片为参考叶片来获取参考叶片温度, 三温模型整体精度较高, 各个观测日拟合方程的斜率多趋近于1 (0.77-1.27), R 2 ≥ 0.81, RMSE ≤ 0.12 mm·h-1 。综合比较不同参考叶片取值方法可知, 选择整个纸片温度最大值作为参考叶片温度时拟合方程的斜率更趋近于1, R 2 整体更大, RMSE 整体更小, 即此时三温模型估算草坪蒸腾精度最优。
为了排除单个观测日数据波动对拟合结果的影响, 进一步对观测期间所有观测数据采用不同参考叶片温度进行分析(图8 ; 表3 ), 发现观测期间所有参考叶片温度取值方法获取的值基本都集中分布在1:1线两侧, 拟合方程的斜率为0.98-1.01, 截距趋近于0 (-0.01- -0.03), R 2 ≥ 0.86, RMSE 为0.078- 0.083 mm·h-1 。
图8
图8
观测期间波文比法与三温模型(3T)不同参考叶片温度取值计算草坪蒸腾速率结果对比。
Fig. 8
Comparison of lawn transpiration rate calculated by Bowen ratio method and three-temperature model (3T) with different reference leaf temperature values during the observation period.
综合对比不同参考叶片温度取值方法可知, 参考温度取参考叶片温度最大值时, 散点分布更加集中, R 2 最大(0.91), RMSE 最小(0.078 mm·h-1 )。
综上所述, 设置干燥绿纸片为参考叶片, 三温模型估算草坪蒸腾的精度总体较高, 其精度因参考叶片温度取值方法而异, 选择不同参考叶片温度对反演效果有影响, 但不显著(p > 0.05)。总体看来, 参考叶片温度选择整个纸片温度最大值时, 三温模型估算结果与波文比观测值拟合效果最好。
2.3 以观测范围内植被温度最大值为参考温度的取值方法
根据2.2 结果可知, 随着参考叶片温度取值变大, 三温模型估算蒸腾的精度总体更优。因此, 本研究进一步尝试直接以地面热红外遥感观测范围内的植被温度最大值为参考温度, 评估这种取值方法的整体效果, 并与设置绿纸片为参考叶片的拟合结果进行对比, 如图9 所示。可以看出, 取各个观测时刻实测植被冠层最高温度为参考温度时, 三温模型估算值与波文比观测值拟合曲线的斜率为1.01, 略大于参考叶片温度最大值的取值方法(0.98); 截距为-0.01, 与参考叶片温度最大值的取值方法相近; R 2 为0.87, 略低于参考叶片温度最大值的取值方法(0.91); RMSE 为0.080 mm·h-1 , 略大于参考叶片温度最大值的取值方法(0.078 mm·h-1 )。由于该取值方法直接假定植被最高温度冠层蒸腾为0 (实际存在一定的蒸腾速率), 容易低估实际蒸腾量。因此, 在地面观测过程中, 建议采用实际测得的参考叶片最高温度进行计算。
图9
图9
观测期间波文比法与三温模型(3T)观测冠层最高温度为参考温度时计算草坪蒸腾速率结果对比。
Fig. 9
Comparison of lawn transpiration rate calculated by Bowen ratio method and three-temperature model (3T) with the maximum temperature of the observed canopy as reference temperature during the observation period.
3 讨论
三温模型蒸腾子模型公式中输入变量的敏感性分析结果表明, 在3个温度参数中参考叶片温度变化对于植被蒸腾计算准确度最为关键。从三温模型原理看, 参考叶片温度是没有蒸腾的参考冠层温度, 即完全干燥没有水分的叶片温度, 实际中用颜色接近的绿色纸片代替。与波文比系统实测结果相比, 设置绿纸片为参考叶片时三温模型估算结果整体精度较高(R 2 ≥ 0.81, RMSE ≤ 0.12 mm·h-1 ); 其中, 参考叶片温度选择为整个纸片温度的最大值时模型估算结果最优(R 2 = 0.91, RMSE = 0.078 mm·h-1 )。直接使用植被冠层温度的最大值为参考温度时, 三温模型估算精度较高(R 2 = 0.87, RMSE = 0.080 mm·h-1 ), 但略低于使用整个参考叶片温度最大值的取值方法, 这是由于该取值方法直接假定植被最高温度冠层蒸腾为0 (实际存在一定的蒸腾速率), 容易低估实际蒸腾量。因此, 考虑到参考叶片设置的局限性, 如果在实际应用中无法或者没有实际测量参考叶片温度时, 使用植被最大温度为参考温度也能达到较好的估算效果。
理论上若土壤水分降至凋萎系数则没有水分供给, 植物开始发生凋萎, 或者植被处于严重胁迫环境, 植被蒸腾受阻, 没有蒸腾潜热的释放, 叶片温度达最大值即参考叶片温度(邱国玉等, 2006 )。由此可判断参考叶片温度是完全干燥叶片能达到的最高温度, 应选择纸片范围内温度最高值, 再结合实际计算结果, 改进三温模型中参考叶片的取值为整个纸片范围上的最大温度值。然而需要注意的是, 该方法估算的蒸散发尽管精度最高, 但考虑到绿色纸片的选取(与实际植被叶片存在色差)、绿色纸片在高湿度条件下的吸湿以及对较大空间尺度范围的代表性等问题(Qiu et al ., 2006 ; Xiong & Qiu, 2014 ; Zhang et al ., 2020 ), 以观测范围内植被温度最大值为参考温度的取值方法更便于三温模型在大尺度蒸腾或蒸散发观测中的推广应用。
在城市化进程迅速的背景下, 城市绿地蒸腾具有显著生态环境效应的事实已经得到广泛认可。然而, 由于城市环境的景观破碎性和绿地的斑块分布, 城市环境中各景观类型组成的复杂下垫面具有高度异质性, 同时植株、地块、城市峡谷、街区、居住区、土地利用区直至整个城市的不同尺度极具复杂性, 城市地表过程变化剧烈, 增加了地表温度、植被等参数反演的不确定性, 城市蒸腾与蒸散发的估算面临严峻挑战(Arnfield, 2003 ; McCabe & Wood, 2006 ; Nouri et al ., 2013 )。相较于其他蒸散发模型, 三温模型已被验证适用于空间异质性更强、微气候环境更加复杂的城市典型绿地蒸腾估算, 且具有其他方法无法替代, 高精度, 易于与遥感结合等独特优势(Qiu et al ., 2020 , 2021 )。通过结合高分辨率热红外成像仪, 三温模型在实际应用中能满足城市绿地蒸腾研究的高空间分辨率要求, 选择合适的参考温度取值方法, 有助于提高三温模型观测城市复杂下垫面环境典型绿地蒸腾估算, 使三温模型在复杂城市环境中的应用更为可靠。同时在较大尺度的遥感应用中, 通过研究得出以观测范围内植被温度最大值为参考温度的取值方法更为有利。
致谢
深圳市知识创新计划(JCYJ20180504165440088)资助。
参考文献
View Option
[1]
Arnfield AJ (2003 ). Two decades of urban climate research: a review of turbulence, exchanges of energy and water, and the urban heat island
International Journal of Climatology , 23 , 1 -26 .
DOI:10.1002/joc.859
URL
[本文引用: 1]
[3]
Bowen IS (1926 ). The ratio of heat losses by conduction and by evaporation from any water surface
Physical Review , 27 , 779 -787 .
DOI:10.1103/PhysRev.27.779
URL
[本文引用: 1]
[4]
Brutsaert W (1986 ). Catchment-scale evaporation and the atmospheric boundary layer
Water Resources Research , 22 , 39 -45 .
[本文引用: 1]
[5]
Burman RD Cuenca RH Weiss A (1983 ). Techniques for estimating irrigation water requirements
Advances in Irrigation , 2 , 335 -394 .
[本文引用: 1]
[7]
Hatfield JL Reginato RJ Idso SB (1983 ). Comparison of long-wave radiation calculation methods over the United States
Water Resources Research , 19 , 285 -288 .
DOI:10.1029/WR019i001p00285
URL
[本文引用: 1]
[8]
Jensen ME Burman RD Allen RG (1990 ). Evapotranspiration and Irrigation Water Requirements
American Society of Civil Engineers, New York . 25 -41 .
[本文引用: 1]
[9]
Lhomme JP Monteny B Amadou M (1994 ). Estimating sensible heat flux from radiometric temperature over sparse millet
Agricultural and Forest Meteorology , 68 , 77 -91 .
DOI:10.1016/0168-1923(94)90070-1
URL
[本文引用: 1]
[10]
Litvak E Manago KF Hogue TS Pataki DE (2017a ). Evapotranspiration of urban landscapes in Los Angeles, California at the municipal scale
Water Resources Research , 53 , 4236 -4252 .
DOI:10.1002/2016WR020254
URL
[本文引用: 1]
[12]
Liu X Li XX Harshan S Roth M Velasco E (2017 ). Evaluation of an urban canopy model in a tropical city: the role of tree evapotranspiration
Environmental Research Letters , 12 , 094008 . DOI: 10.1088/1748-9326/aa7ee7 .
DOI:10.1088/1748-9326/aa7ee7
URL
[本文引用: 1]
[13]
McCabe MF Wood EF (2006 ). Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors
Remote Sensing of Environment , 105 , 271 -285 .
DOI:10.1016/j.rse.2006.07.006
URL
[本文引用: 2]
[14]
Monteith JL Unsworth MH (2013 ). Principles of Environmental Physics: Plants, Animals and the Atmosphere . Academic Press , New York .
[本文引用: 1]
[15]
Nouri H Beecham S Kazemi F Hassanli AM (2013 ). A review of ET measurement techniques for estimating the water requirements of urban landscape vegetation
Urban Water Journal , 10 , 247 -259 .
DOI:10.1080/1573062X.2012.726360
URL
[本文引用: 1]
[16]
Qiu GY (1996 ). A New Method for Estimation of Evapotranspiration
PhD dissertation, United Graduate School of Agriculture Science, Tottori University, Tottori, Japan .
[本文引用: 3]
[17]
Qiu GY Momii K Yano T Lascano RJ (1999 ). Experimental verification of a mechanistic model to partition evapotranspiration into soil water and plant evaporation
Agricultural and Forest Meteorology , 93 (2 ), 79 -93 .
DOI:10.1016/S0168-1923(98)00115-4
URL
[本文引用: 2]
[18]
Qiu GY Sase S Shi P Ding G (2003 ). Theoretical analysis and experimental verification of a remotely measurable plant transpiration transfer coefficient
Japan Agricultural Research Quarterly , 37 (3 ), 141 -149 .
DOI:10.6090/jarq.37.141
URL
[本文引用: 1]
[19]
Qiu GY Shi PJ Wang LM (2006 ). Theoretical analysis of a remotely measurable soil evaporation transfer coefficient
Remote sensing of Environment , 101 , 390 -398 .
DOI:10.1016/j.rse.2006.01.007
URL
[本文引用: 4]
[20]
Qiu GY Tan SL Wang Y Yu XH Yan CH (2017 ). Characteristics of evapotranspiration of urban lawns in a sub-tropical megacity and its measurement by the “three temperature model + infrared remote sensing” method
Remote Sensing , 9 , 502 . DOI: 10.3390/rs9050502 .
DOI:10.3390/rs9050502
URL
[本文引用: 1]
[21]
Qiu GY Wang B Li T Zhang XN Zou ZD Yan CH (2021 ). Estimation of the transpiration of urban shrubs using the modified three-dimensional three-temperature model and infrared remote sensing
Journal of Hydrology , 594 , 125940 . DOI: 10.1016/j.jhydrol.2020.125940 .
DOI:10.1016/j.jhydrol.2020.125940
URL
[本文引用: 2]
[22]
Qiu GY Wu X Wang S Song XF (2006 ). Three temperature (3T) model—A method to estimate evapotranspiration and evaluate environmental quality based on surface temperature. IV. Plant transpiration transfer coefficient
Journal of Plant Ecology (Chinese Version ) , 30 , 852 -860 .
[本文引用: 1]
[ 邱国玉 , 吴晓 , 王帅 , 宋献方 (2006 ). 三温模型——基于表面温度测算蒸散和评价环境质量的方法IV. 植被蒸腾扩散系数
植物生态学报 , 30 , 852 -860 .]
DOI:10.17521/cjpe.2006.0108
[本文引用: 1]
作为蒸散量的测算和环境评价的一种方法,通过近年来对三温模型的研究,该文详细探讨了植被蒸腾扩散系数(hat),并通过实验验证了它在不同环境条件下的特性和应用前景。在该模型中,hat的表示式为hat=(Tc-Ta)/( Tp-Ta),式中Tc、Tp和Ta分别为冠层温度、没有蒸腾(蒸腾量为零)的冠层温度和气温。理论上,植被蒸腾扩散系数的取值范围为hat≤1,hat的取值范围可以决定植被蒸腾量的大小,该系数越小, 蒸腾量越大。为了证明hat的这些特性,在1994~1999年的5年间,用3种作物(高粱(Sorghum bicolor),番茄( Lycopersicon esculentum)和甜瓜(Cucumis melo))进行了5次试验。实验结果表明: hat值与感热通量比率(H/Hp)的值近似相等,二者之间回归线的斜率接近为1,截距接近0,回归系数为r2=0.70。此外,hat值不仅能较好地反映植物根系区的土壤水分状况、也能较好地反应天气状况。在缺水条件下,hat主要受根部区域的水分状况影响。 所以,hat可作为作物水分亏缺的指标。当植被受到其它环境胁迫(污染、高温等)时,hat可作为评价环境质量的指标。植被蒸腾扩散系数的主要优点不仅是能很好地反映蒸腾过程和确定蒸腾量,而且容易测得,便于遥感应用。
[23]
Qiu GY Xiong YJ (2014 ). Water Versus Energy: Evapotranspiration, Thermal Environment and Energy Budget . Science Press , Beijing .
[本文引用: 1]
[ 邱国玉 , 熊育久 (2014 ). 水与能: 蒸散发, 热环境及其能量收支 . 科学出版社 , 北京 .]
[本文引用: 1]
[24]
Qiu GY Yano T Momii K (1998 ). An improved methodology to measure evaporation from bare soil based on comparison of surface temperature with a dry soil surface
Journal of Hydrology , 210 , 93 -105 .
DOI:10.1016/S0022-1694(98)00174-7
URL
[本文引用: 3]
[25]
Qiu GY Yu XH Wen HY Yan CH (2020 ). An advanced approach for measuring the transpiration rate of individual urban trees by the 3D three-temperature model and thermal infrared remote sensing
Journal of Hydrology , 587 , 125034 . DOI: 10.1016/j.jhydrol.2020.125034 .
DOI:10.1016/j.jhydrol.2020.125034
URL
[本文引用: 2]
[27]
Xia J Shi W Wang Q Zou L (2017 ). Discussion of several hydrological issues regarding sponge city construction
Water Resources Protection , 33 (1 ), 1 -8 .
[本文引用: 1]
[ 夏军 , 石卫 , 王强 , 邹磊 (2017 ). 海绵城市建设中若干水文学问题的研讨
水资源保护 , 33 (1 ), 1 -8 .]
[本文引用: 1]
[28]
Xiong YJ Qiu GY (2014 ). Simplifying the revised three- temperature model for remotely estimating regional evapotranspiration and its application to a semi-arid steppe
International Journal of Remote Sensing , 35 , 2003 -2027 .
DOI:10.1080/01431161.2014.885149
URL
[本文引用: 2]
[29]
Yan C Qiu GY (2016 ). The three-temperature model to estimate evapotranspiration and its partitioning at multiple scales: a review
Transactions of the ASABE , 59 , 661 -670 .
DOI:10.13031/trans.59.11087
URL
[本文引用: 1]
[30]
Yu XH Yang YJ Tan SL Li RL Qin HP Qiu GY (2017 ). Evapotranspiration and its cooling effect of urban green roof
Chinese Journal of Environmental Engineering , 11 , 5333 -5340 .
[本文引用: 1]
[ 于小惠 , 杨雅君 , 谭圣林 , 李瑞利 , 秦华鹏 , 邱国玉 (2017 ). 绿色屋顶蒸散发及其降温效果
环境工程学报 , 11 , 5333 -5340 .]
[本文引用: 1]
[31]
Zhang YY Qin HP Zhang JY Hu YC (2020 ). An in situ measurement method of evapotranspiration from typical LID facilities based on the three-temperature model
Journal of Hydrology , 588 . DOI: 10.1016/j.jhydrol.2020.125105 .
DOI:10.1016/j.jhydrol.2020.125105
[本文引用: 1]
[32]
Zou ZD Yang YJ Qiu GY (2019 ). Quantifying the evapotranspiration rate and its cooling effects of urban hedges based on three-temperature model and infrared remote sensing
Remote Sensing , 11 , 202 . DOI: 10.3390/rs11020202 .
DOI:10.3390/rs11020202
URL
[本文引用: 1]
Two decades of urban climate research: a review of turbulence, exchanges of energy and water, and the urban heat island
1
2003
... 在城市化进程迅速的背景下, 城市绿地蒸腾具有显著生态环境效应的事实已经得到广泛认可.然而, 由于城市环境的景观破碎性和绿地的斑块分布, 城市环境中各景观类型组成的复杂下垫面具有高度异质性, 同时植株、地块、城市峡谷、街区、居住区、土地利用区直至整个城市的不同尺度极具复杂性, 城市地表过程变化剧烈, 增加了地表温度、植被等参数反演的不确定性, 城市蒸腾与蒸散发的估算面临严峻挑战(Arnfield, 2003 ; McCabe & Wood, 2006 ; Nouri et al ., 2013 ).相较于其他蒸散发模型, 三温模型已被验证适用于空间异质性更强、微气候环境更加复杂的城市典型绿地蒸腾估算, 且具有其他方法无法替代, 高精度, 易于与遥感结合等独特优势(Qiu et al ., 2020 , 2021 ).通过结合高分辨率热红外成像仪, 三温模型在实际应用中能满足城市绿地蒸腾研究的高空间分辨率要求, 选择合适的参考温度取值方法, 有助于提高三温模型观测城市复杂下垫面环境典型绿地蒸腾估算, 使三温模型在复杂城市环境中的应用更为可靠.同时在较大尺度的遥感应用中, 通过研究得出以观测范围内植被温度最大值为参考温度的取值方法更为有利. ...
A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates
3
1979
... 为了解输入参数对三温模型计算结果的影响程度, 对三温模型做敏感性分析, 对于提高三温模型计算准确性十分必要.本研究采用Beven (1979 )提出的敏感性分析方法, 具体如下: ...
... 式中, 差分$\partial (\text{LE})\text{/}\partial {{p}_{i}}$ ${{S}_{i}}$ ) 定义为(Beven, 1979 ): ...
... 式中, Si 表示参数pi 的变化引起LE的变化, 例如Si 为0.1时, 表明参数pi 增加10%时预期LE可能增加1%.系数为负表示pi 的增加会导致LE降低.公式(21)对LE和pi 的大小敏感, 特别是如果LE或pi 各自趋向于零, 或者pi 取值的范围与其大小相比很小, 则Si 可能不能很好地指示pi 对LE影响的显著性(Beven, 1979 ). ...
The ratio of heat losses by conduction and by evaporation from any water surface
1
1926
... 波文比-能量平衡法(Bowen ratio energy balance)是Bowen在1926 年提出的蒸散发计算方法.其原理是根据能量守恒定律, 植被冠层接收的太阳辐射能量等于各途径支出的能量总和, 能量平衡方程为: ...
Catchment-scale evaporation and the atmospheric boundary layer
1
1986
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
Techniques for estimating irrigation water requirements
1
1983
... 式中, α 为参考叶片反照率, 取值0.22; Rs,cp 为参考叶片上短波太阳辐射(W∙m-2 ), 可以通过波文比系统直接观测; ΔR1,cp 为参考叶片上净长波辐射(W∙m-2 ), 由下述公式(Weiss, 1982 ; Burman et al ., 1983 )计算得出: ...
A review of flux-profile relationships
1
1974
... 在某一界面上, 显热通量与潜热通量的比值被定义为波文比(β ), β 可以表示为垂直方向上温度梯度和湿度梯度的函数.假定乱流水汽湍流交换系数(K w )和乱流热交换系数(K h )相等(Dyer, 1974 ), β 可以定义为: ...
Comparison of long-wave radiation calculation methods over the United States
1
1983
... 式中, Rss 为晴天的太阳辐射(W∙m-2 ), ε cp 为参考叶片表面反射率, 本研究取值0.98, σ 表示Stefan-Boltzman常数(5.675 × 10-8 J∙m-2 ∙K-4 ∙s-1 ).观测当天为晴天, Rs ≈ Rss , 那么0.4 + 0.6 Rs /Rss ≈ 1.ε a 为大气发射率, 可表示为(Hatfield et al ., 1983 ): εa = 0.92 × 10 -5 T a 2 . ...
Evapotranspiration and Irrigation Water Requirements
1
1990
... 式中, Rn,c 和T a 可以直接通过波文比系统获取; T c 可以通过解译草坪的热红外图像获取; T cp 从作为参考叶片的纸片的温度上取值; 参考叶片净辐射(Rn,cp , W∙m-2 )可由以下公式(Jensen et al ., 1990 )计算: ...
Estimating sensible heat flux from radiometric temperature over sparse millet
1
1994
... 三温模型反演与分离蒸散发组分(蒸发与蒸腾)的关键包括: 1)蒸发、蒸腾系数物理取值的合理范围(边界)的确定; 2)植被与土壤组分温度的确定; 3)参考土壤与参考植被温度的确定.目前研究已明确三温模型中植被蒸腾扩散系数、土壤蒸发扩散系数的边界(Qiu et al ., 2003 , 2006 ), 植被与土壤组分温度的确定也有较为成熟的方法(Lhomme et al ., 1994 ), 而参考温度的参数化过程一直是三温模型反演土壤蒸发和植被蒸腾面临的难点.三温模型应用于估算空间异质性更强、微气候环境更加复杂的城市绿地蒸腾时, 参考温度参数化对三温模型应用于城市复杂下垫面环境典型绿地蒸腾估算的精度及适用性的影响如何? 这一关键科学问题亟待研究. ...
Evapotranspiration of urban landscapes in Los Angeles, California at the municipal scale
1
2017a
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
A method for estimating transpiration of irrigated urban trees in California
1
2017b
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
Evaluation of an urban canopy model in a tropical city: the role of tree evapotranspiration
1
2017
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors
2
2006
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
... 在城市化进程迅速的背景下, 城市绿地蒸腾具有显著生态环境效应的事实已经得到广泛认可.然而, 由于城市环境的景观破碎性和绿地的斑块分布, 城市环境中各景观类型组成的复杂下垫面具有高度异质性, 同时植株、地块、城市峡谷、街区、居住区、土地利用区直至整个城市的不同尺度极具复杂性, 城市地表过程变化剧烈, 增加了地表温度、植被等参数反演的不确定性, 城市蒸腾与蒸散发的估算面临严峻挑战(Arnfield, 2003 ; McCabe & Wood, 2006 ; Nouri et al ., 2013 ).相较于其他蒸散发模型, 三温模型已被验证适用于空间异质性更强、微气候环境更加复杂的城市典型绿地蒸腾估算, 且具有其他方法无法替代, 高精度, 易于与遥感结合等独特优势(Qiu et al ., 2020 , 2021 ).通过结合高分辨率热红外成像仪, 三温模型在实际应用中能满足城市绿地蒸腾研究的高空间分辨率要求, 选择合适的参考温度取值方法, 有助于提高三温模型观测城市复杂下垫面环境典型绿地蒸腾估算, 使三温模型在复杂城市环境中的应用更为可靠.同时在较大尺度的遥感应用中, 通过研究得出以观测范围内植被温度最大值为参考温度的取值方法更为有利. ...
1
2013
... 式中, LEc 为植被潜热通量, Rn,c 为植被表面净辐射, Hc 为植被表面显热通量, 各参数单位与公式(1)中一致.公式(2)经过参数替换后, Hc 可表示为(Monteith & Unsworth, 2013 ): ...
A review of ET measurement techniques for estimating the water requirements of urban landscape vegetation
1
2013
... 在城市化进程迅速的背景下, 城市绿地蒸腾具有显著生态环境效应的事实已经得到广泛认可.然而, 由于城市环境的景观破碎性和绿地的斑块分布, 城市环境中各景观类型组成的复杂下垫面具有高度异质性, 同时植株、地块、城市峡谷、街区、居住区、土地利用区直至整个城市的不同尺度极具复杂性, 城市地表过程变化剧烈, 增加了地表温度、植被等参数反演的不确定性, 城市蒸腾与蒸散发的估算面临严峻挑战(Arnfield, 2003 ; McCabe & Wood, 2006 ; Nouri et al ., 2013 ).相较于其他蒸散发模型, 三温模型已被验证适用于空间异质性更强、微气候环境更加复杂的城市典型绿地蒸腾估算, 且具有其他方法无法替代, 高精度, 易于与遥感结合等独特优势(Qiu et al ., 2020 , 2021 ).通过结合高分辨率热红外成像仪, 三温模型在实际应用中能满足城市绿地蒸腾研究的高空间分辨率要求, 选择合适的参考温度取值方法, 有助于提高三温模型观测城市复杂下垫面环境典型绿地蒸腾估算, 使三温模型在复杂城市环境中的应用更为可靠.同时在较大尺度的遥感应用中, 通过研究得出以观测范围内植被温度最大值为参考温度的取值方法更为有利. ...
A New Method for Estimation of Evapotranspiration
3
1996
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
... 目前三温模型反演植被蒸腾中参考温度参数化的方法主要有3种: 1)实测法, 即以干燥的绿色树叶、纸片等为参考叶片, 通过热红外温度传感器或者热红外成像仪直接观测(Qiu, 1996 ), 但参考叶片温度的不同取值方法使其具有不确定性; 2)植被与土壤组分温度最值法, 如根据卫星或地面热红外遥感测算的植被与土壤组分温度, 取植被像元温度的最大值作为参考植被温度(Xiong & Qiu, 2014 ), 此时温度最大值的确定受温度图像代表范围, 以及组分温度分离精度等影响; 3)地表温度最值法, 即直接以热红外地表温度(不区分组分温度)最大值为参考温度(Qiu et al ., 1998 ), 在干旱、半干旱区通常对应干燥土壤, 但在湿润区有待检验.基于以上研究现状, 当三温模型推广应用时, 需要深入细致地研究其各输入变量尤其是参考温度的参数化过程. ...
... 邱国玉提出的三温模型(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 )是一种测算蒸散发和评估环境质量的方法, 因为该模型的核心参数是表面温度、参考表面温度和气温, 故被称为三温模型.本研究仅用到植被蒸腾模型. ...
Experimental verification of a mechanistic model to partition evapotranspiration into soil water and plant evaporation
2
1999
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
... 邱国玉提出的三温模型(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 )是一种测算蒸散发和评估环境质量的方法, 因为该模型的核心参数是表面温度、参考表面温度和气温, 故被称为三温模型.本研究仅用到植被蒸腾模型. ...
Theoretical analysis and experimental verification of a remotely measurable plant transpiration transfer coefficient
1
2003
... 三温模型反演与分离蒸散发组分(蒸发与蒸腾)的关键包括: 1)蒸发、蒸腾系数物理取值的合理范围(边界)的确定; 2)植被与土壤组分温度的确定; 3)参考土壤与参考植被温度的确定.目前研究已明确三温模型中植被蒸腾扩散系数、土壤蒸发扩散系数的边界(Qiu et al ., 2003 , 2006 ), 植被与土壤组分温度的确定也有较为成熟的方法(Lhomme et al ., 1994 ), 而参考温度的参数化过程一直是三温模型反演土壤蒸发和植被蒸腾面临的难点.三温模型应用于估算空间异质性更强、微气候环境更加复杂的城市绿地蒸腾时, 参考温度参数化对三温模型应用于城市复杂下垫面环境典型绿地蒸腾估算的精度及适用性的影响如何? 这一关键科学问题亟待研究. ...
Theoretical analysis of a remotely measurable soil evaporation transfer coefficient
4
2006
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
... 三温模型反演与分离蒸散发组分(蒸发与蒸腾)的关键包括: 1)蒸发、蒸腾系数物理取值的合理范围(边界)的确定; 2)植被与土壤组分温度的确定; 3)参考土壤与参考植被温度的确定.目前研究已明确三温模型中植被蒸腾扩散系数、土壤蒸发扩散系数的边界(Qiu et al ., 2003 , 2006 ), 植被与土壤组分温度的确定也有较为成熟的方法(Lhomme et al ., 1994 ), 而参考温度的参数化过程一直是三温模型反演土壤蒸发和植被蒸腾面临的难点.三温模型应用于估算空间异质性更强、微气候环境更加复杂的城市绿地蒸腾时, 参考温度参数化对三温模型应用于城市复杂下垫面环境典型绿地蒸腾估算的精度及适用性的影响如何? 这一关键科学问题亟待研究. ...
... 邱国玉提出的三温模型(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 )是一种测算蒸散发和评估环境质量的方法, 因为该模型的核心参数是表面温度、参考表面温度和气温, 故被称为三温模型.本研究仅用到植被蒸腾模型. ...
... 理论上若土壤水分降至凋萎系数则没有水分供给, 植物开始发生凋萎, 或者植被处于严重胁迫环境, 植被蒸腾受阻, 没有蒸腾潜热的释放, 叶片温度达最大值即参考叶片温度(邱国玉等, 2006 ).由此可判断参考叶片温度是完全干燥叶片能达到的最高温度, 应选择纸片范围内温度最高值, 再结合实际计算结果, 改进三温模型中参考叶片的取值为整个纸片范围上的最大温度值.然而需要注意的是, 该方法估算的蒸散发尽管精度最高, 但考虑到绿色纸片的选取(与实际植被叶片存在色差)、绿色纸片在高湿度条件下的吸湿以及对较大空间尺度范围的代表性等问题(Qiu et al ., 2006 ; Xiong & Qiu, 2014 ; Zhang et al ., 2020 ), 以观测范围内植被温度最大值为参考温度的取值方法更便于三温模型在大尺度蒸腾或蒸散发观测中的推广应用. ...
Characteristics of evapotranspiration of urban lawns in a sub-tropical megacity and its measurement by the “three temperature model + infrared remote sensing” method
1
2017
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
Estimation of the transpiration of urban shrubs using the modified three-dimensional three-temperature model and infrared remote sensing
2
2021
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
... 在城市化进程迅速的背景下, 城市绿地蒸腾具有显著生态环境效应的事实已经得到广泛认可.然而, 由于城市环境的景观破碎性和绿地的斑块分布, 城市环境中各景观类型组成的复杂下垫面具有高度异质性, 同时植株、地块、城市峡谷、街区、居住区、土地利用区直至整个城市的不同尺度极具复杂性, 城市地表过程变化剧烈, 增加了地表温度、植被等参数反演的不确定性, 城市蒸腾与蒸散发的估算面临严峻挑战(Arnfield, 2003 ; McCabe & Wood, 2006 ; Nouri et al ., 2013 ).相较于其他蒸散发模型, 三温模型已被验证适用于空间异质性更强、微气候环境更加复杂的城市典型绿地蒸腾估算, 且具有其他方法无法替代, 高精度, 易于与遥感结合等独特优势(Qiu et al ., 2020 , 2021 ).通过结合高分辨率热红外成像仪, 三温模型在实际应用中能满足城市绿地蒸腾研究的高空间分辨率要求, 选择合适的参考温度取值方法, 有助于提高三温模型观测城市复杂下垫面环境典型绿地蒸腾估算, 使三温模型在复杂城市环境中的应用更为可靠.同时在较大尺度的遥感应用中, 通过研究得出以观测范围内植被温度最大值为参考温度的取值方法更为有利. ...
三温模型——基于表面温度测算蒸散和评价环境质量的方法IV. 植被蒸腾扩散系数
1
2006
... 理论上若土壤水分降至凋萎系数则没有水分供给, 植物开始发生凋萎, 或者植被处于严重胁迫环境, 植被蒸腾受阻, 没有蒸腾潜热的释放, 叶片温度达最大值即参考叶片温度(邱国玉等, 2006 ).由此可判断参考叶片温度是完全干燥叶片能达到的最高温度, 应选择纸片范围内温度最高值, 再结合实际计算结果, 改进三温模型中参考叶片的取值为整个纸片范围上的最大温度值.然而需要注意的是, 该方法估算的蒸散发尽管精度最高, 但考虑到绿色纸片的选取(与实际植被叶片存在色差)、绿色纸片在高湿度条件下的吸湿以及对较大空间尺度范围的代表性等问题(Qiu et al ., 2006 ; Xiong & Qiu, 2014 ; Zhang et al ., 2020 ), 以观测范围内植被温度最大值为参考温度的取值方法更便于三温模型在大尺度蒸腾或蒸散发观测中的推广应用. ...
三温模型——基于表面温度测算蒸散和评价环境质量的方法IV. 植被蒸腾扩散系数
1
2006
... 理论上若土壤水分降至凋萎系数则没有水分供给, 植物开始发生凋萎, 或者植被处于严重胁迫环境, 植被蒸腾受阻, 没有蒸腾潜热的释放, 叶片温度达最大值即参考叶片温度(邱国玉等, 2006 ).由此可判断参考叶片温度是完全干燥叶片能达到的最高温度, 应选择纸片范围内温度最高值, 再结合实际计算结果, 改进三温模型中参考叶片的取值为整个纸片范围上的最大温度值.然而需要注意的是, 该方法估算的蒸散发尽管精度最高, 但考虑到绿色纸片的选取(与实际植被叶片存在色差)、绿色纸片在高湿度条件下的吸湿以及对较大空间尺度范围的代表性等问题(Qiu et al ., 2006 ; Xiong & Qiu, 2014 ; Zhang et al ., 2020 ), 以观测范围内植被温度最大值为参考温度的取值方法更便于三温模型在大尺度蒸腾或蒸散发观测中的推广应用. ...
1
2014
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
1
2014
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
An improved methodology to measure evaporation from bare soil based on comparison of surface temperature with a dry soil surface
3
1998
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
... 目前三温模型反演植被蒸腾中参考温度参数化的方法主要有3种: 1)实测法, 即以干燥的绿色树叶、纸片等为参考叶片, 通过热红外温度传感器或者热红外成像仪直接观测(Qiu, 1996 ), 但参考叶片温度的不同取值方法使其具有不确定性; 2)植被与土壤组分温度最值法, 如根据卫星或地面热红外遥感测算的植被与土壤组分温度, 取植被像元温度的最大值作为参考植被温度(Xiong & Qiu, 2014 ), 此时温度最大值的确定受温度图像代表范围, 以及组分温度分离精度等影响; 3)地表温度最值法, 即直接以热红外地表温度(不区分组分温度)最大值为参考温度(Qiu et al ., 1998 ), 在干旱、半干旱区通常对应干燥土壤, 但在湿润区有待检验.基于以上研究现状, 当三温模型推广应用时, 需要深入细致地研究其各输入变量尤其是参考温度的参数化过程. ...
... 邱国玉提出的三温模型(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 )是一种测算蒸散发和评估环境质量的方法, 因为该模型的核心参数是表面温度、参考表面温度和气温, 故被称为三温模型.本研究仅用到植被蒸腾模型. ...
An advanced approach for measuring the transpiration rate of individual urban trees by the 3D three-temperature model and thermal infrared remote sensing
2
2020
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
... 在城市化进程迅速的背景下, 城市绿地蒸腾具有显著生态环境效应的事实已经得到广泛认可.然而, 由于城市环境的景观破碎性和绿地的斑块分布, 城市环境中各景观类型组成的复杂下垫面具有高度异质性, 同时植株、地块、城市峡谷、街区、居住区、土地利用区直至整个城市的不同尺度极具复杂性, 城市地表过程变化剧烈, 增加了地表温度、植被等参数反演的不确定性, 城市蒸腾与蒸散发的估算面临严峻挑战(Arnfield, 2003 ; McCabe & Wood, 2006 ; Nouri et al ., 2013 ).相较于其他蒸散发模型, 三温模型已被验证适用于空间异质性更强、微气候环境更加复杂的城市典型绿地蒸腾估算, 且具有其他方法无法替代, 高精度, 易于与遥感结合等独特优势(Qiu et al ., 2020 , 2021 ).通过结合高分辨率热红外成像仪, 三温模型在实际应用中能满足城市绿地蒸腾研究的高空间分辨率要求, 选择合适的参考温度取值方法, 有助于提高三温模型观测城市复杂下垫面环境典型绿地蒸腾估算, 使三温模型在复杂城市环境中的应用更为可靠.同时在较大尺度的遥感应用中, 通过研究得出以观测范围内植被温度最大值为参考温度的取值方法更为有利. ...
An experimental study of net radiation, its components and prediction
1
1982
... 式中, α 为参考叶片反照率, 取值0.22; Rs,cp 为参考叶片上短波太阳辐射(W∙m-2 ), 可以通过波文比系统直接观测; ΔR1,cp 为参考叶片上净长波辐射(W∙m-2 ), 由下述公式(Weiss, 1982 ; Burman et al ., 1983 )计算得出: ...
海绵城市建设中若干水文学问题的研讨
1
2017
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
海绵城市建设中若干水文学问题的研讨
1
2017
... 蒸散发(ET)主要包括植物蒸腾、土壤蒸发和自由水面蒸发, 是陆地生态系统中土壤-植被-大气连续体水分消耗的主要途径, 是地球水分及能量循环的主要环节(McCabe & Wood, 2006 ; 邱国玉和熊育久, 2014 ).随着全球城市化的高速发展, 城市下垫面的剧烈改变导致一系列城市热环境问题的出现, 诸如热岛效应、洪旱、强降雨、热浪等极端事件均与蒸散发密不可分(Brutsaert, 1986 ).作为联结城市能量平衡与水量平衡的纽带, 城市蒸散发估算对于城市水资源管理、城市水文研究与热环境调控研究具有重要意义, 准确估算城市绿地蒸腾也成为近年来城市生态水文、城市热环境调控以及城市规划、设计与管理领域的研究热点(Litvak et al ., 2017a , 2017b ; Liu et al ., 2017 ; 夏军等, 2017 ). ...
Simplifying the revised three- temperature model for remotely estimating regional evapotranspiration and its application to a semi-arid steppe
2
2014
... 目前三温模型反演植被蒸腾中参考温度参数化的方法主要有3种: 1)实测法, 即以干燥的绿色树叶、纸片等为参考叶片, 通过热红外温度传感器或者热红外成像仪直接观测(Qiu, 1996 ), 但参考叶片温度的不同取值方法使其具有不确定性; 2)植被与土壤组分温度最值法, 如根据卫星或地面热红外遥感测算的植被与土壤组分温度, 取植被像元温度的最大值作为参考植被温度(Xiong & Qiu, 2014 ), 此时温度最大值的确定受温度图像代表范围, 以及组分温度分离精度等影响; 3)地表温度最值法, 即直接以热红外地表温度(不区分组分温度)最大值为参考温度(Qiu et al ., 1998 ), 在干旱、半干旱区通常对应干燥土壤, 但在湿润区有待检验.基于以上研究现状, 当三温模型推广应用时, 需要深入细致地研究其各输入变量尤其是参考温度的参数化过程. ...
... 理论上若土壤水分降至凋萎系数则没有水分供给, 植物开始发生凋萎, 或者植被处于严重胁迫环境, 植被蒸腾受阻, 没有蒸腾潜热的释放, 叶片温度达最大值即参考叶片温度(邱国玉等, 2006 ).由此可判断参考叶片温度是完全干燥叶片能达到的最高温度, 应选择纸片范围内温度最高值, 再结合实际计算结果, 改进三温模型中参考叶片的取值为整个纸片范围上的最大温度值.然而需要注意的是, 该方法估算的蒸散发尽管精度最高, 但考虑到绿色纸片的选取(与实际植被叶片存在色差)、绿色纸片在高湿度条件下的吸湿以及对较大空间尺度范围的代表性等问题(Qiu et al ., 2006 ; Xiong & Qiu, 2014 ; Zhang et al ., 2020 ), 以观测范围内植被温度最大值为参考温度的取值方法更便于三温模型在大尺度蒸腾或蒸散发观测中的推广应用. ...
The three-temperature model to estimate evapotranspiration and its partitioning at multiple scales: a review
1
2016
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
绿色屋顶蒸散发及其降温效果
1
2017
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
绿色屋顶蒸散发及其降温效果
1
2017
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...
An in situ measurement method of evapotranspiration from typical LID facilities based on the three-temperature model
1
2020
... 理论上若土壤水分降至凋萎系数则没有水分供给, 植物开始发生凋萎, 或者植被处于严重胁迫环境, 植被蒸腾受阻, 没有蒸腾潜热的释放, 叶片温度达最大值即参考叶片温度(邱国玉等, 2006 ).由此可判断参考叶片温度是完全干燥叶片能达到的最高温度, 应选择纸片范围内温度最高值, 再结合实际计算结果, 改进三温模型中参考叶片的取值为整个纸片范围上的最大温度值.然而需要注意的是, 该方法估算的蒸散发尽管精度最高, 但考虑到绿色纸片的选取(与实际植被叶片存在色差)、绿色纸片在高湿度条件下的吸湿以及对较大空间尺度范围的代表性等问题(Qiu et al ., 2006 ; Xiong & Qiu, 2014 ; Zhang et al ., 2020 ), 以观测范围内植被温度最大值为参考温度的取值方法更便于三温模型在大尺度蒸腾或蒸散发观测中的推广应用. ...
Quantifying the evapotranspiration rate and its cooling effects of urban hedges based on three-temperature model and infrared remote sensing
1
2019
... 三温模型(the three-temperature model)是由邱国玉提出的一种测算土壤蒸发和植被蒸腾以及评价环境质量的方法(Qiu, 1996 ; Qiu et al ., 1998 , 1999 , 2006 ).它以地表能量平衡方程为基础, 通过引入参考土壤(干燥、无蒸发的土壤)和参考植被(干燥、无蒸腾的植被), 避开了空气动力学阻抗等带来的复杂计算和系统误差, 简化了土壤蒸发和植被蒸腾计算的过程, 提高了植被蒸腾计算的精度, 同时易于与遥感结合应用, 被广泛应用于高异质性的干旱半干旱地区不同尺度和不同下垫面条件下的蒸发、蒸腾观测(Yan & Qiu, 2016 ), 近年来, 三温模型在城市草坪(Qiu et al ., 2017 )、城市灌木(Zou et al ., 2019 ; Qiu et al ., 2021 )、城市乔木(Qiu et al ., 2020 )、绿色屋顶(于小惠等, 2017 )等不同尺度的植被蒸腾研究中也均取得较好的应用效果. ...