
|
|
||
|
一种基于数码相机图像和群落冠层结构调查的草地地上生物量估算方法
植物生态学报
2022, 46 (10):
1280-1288.
DOI: 10.17521/cjpe.2022.0235
草地地上生物量是影响其生态系统功能最重要的因素之一, 也是草地生态学研究中不可或缺的监测指标。草地地上生物量监测多采用收割法进行, 但这种破坏性取样方法会对研究区域带来巨大干扰, 尤其是面积较小的长期定位监测或者控制实验研究样地, 从而使得地上生物量监测的频次受到很大限制。因此, 通过获取某些原位易测变量, 建立地上生物量的估算方法具有重要意义。该研究依托内蒙古典型草地刈割控制实验平台, 通过数码照片获取不同土地利用方式下的植被覆盖度, 并对样方内的叶面积指数、植被高度、物种多样性等参数进行了测定, 最后利用一元回归模型、逐步回归模型和随机森林模型对地上生物量进行估算。结果表明, 植被覆盖度、叶面积指数、植被平均高度、植被最大高度和物种丰富度是影响地上生物量的主要驱动因素。通过构建适宜于本地的逐步回归模型, 可以实现草地地上生物量的准确预测。在该研究区域中, 预测模型的决定系数(R2) = 0.91, 均方根误差(RMSE) = 35.60 g·m-2。该研究提供了一种快速、准确且非破坏性测定草地地上生物量的方法, 可作为传统收割法的有效补充。 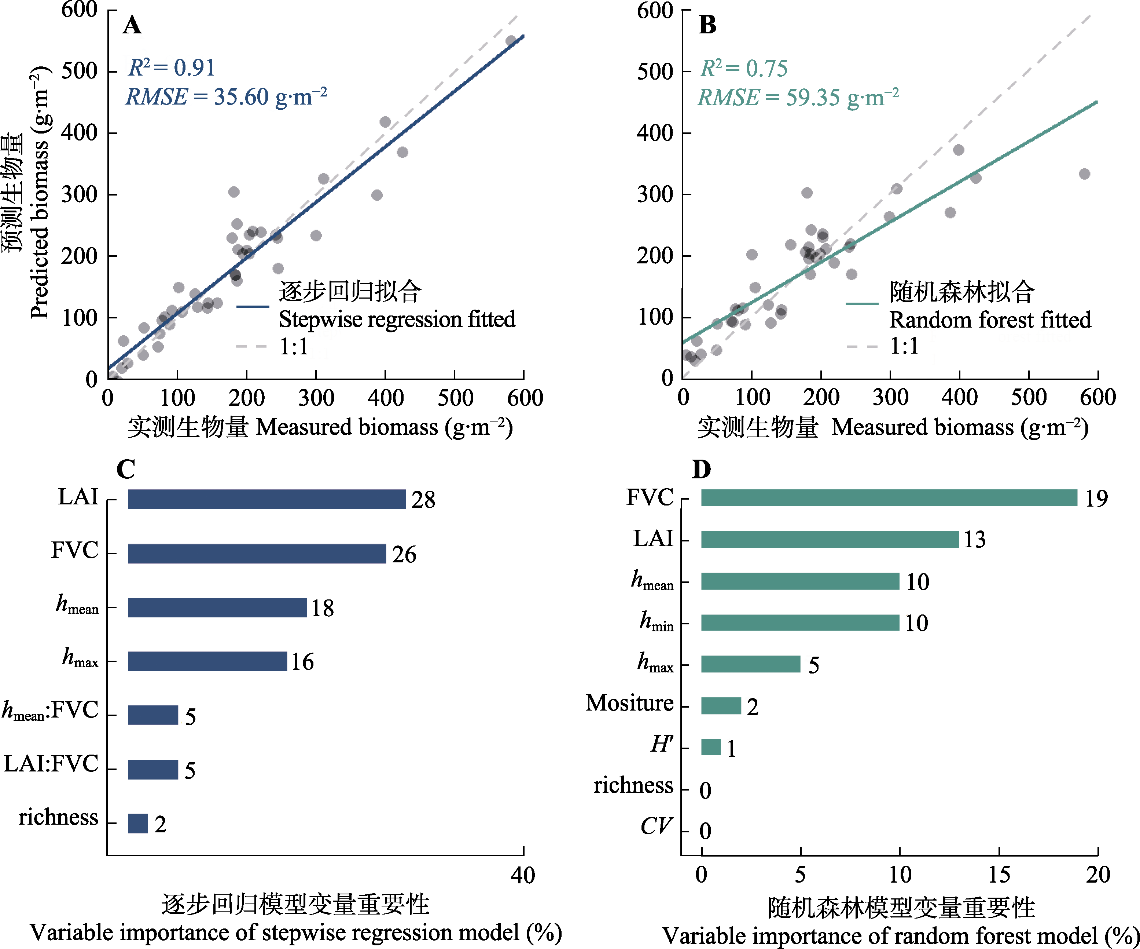 View image in article
图4
草地地上生物量预测模型及变量相对重要性。蓝色实线代表逐步回归模型(A)的拟合线, 绿色实线代表随机森林模型(B)的拟合线, 灰色虚线为1:1线, 对应模型的决定系数(R2)和均方根误差(RMSE)在左上角进行标示。模型变量重要性: 逐步回归模型(C), 随机森林模型(D)。条柱旁边的数字代表变量对应的相对重要性, 冒号连接的变量代表变量间的交互作用; 逐步回归模型的变量重要性来源于不同变量对R2的贡献, 随机森林模型的变量重要性来源于均值递减精度的方法。CV, 高度变异系数; FVC, 植被覆盖度; hmean, 植被平均高度; hmax, 植被最大高度; hmin, 植被最小高度; H', 香农-维纳多样性指数; LAI, 叶面积指数。
正文中引用本图/表的段落
此外, 本研究使用交叉验证, 对每个模型的泛化能力表现进行了评估(Stone, 1977)。首先, 对所有样本进行多次随机抽样, 依次随机抽取70%、72%、74%、76%、78%、80%的样本用于模型训练, 剩余样本作为测试样本对训练模型进行验证。然后, 通过计算预测生物量和实测生物量之间的R2和RMSE来评估模型的泛化能力(附录图A-N)。以上所有分析均由R 4.0.5软件实现。
使用LAI、植被平均高度、植被覆盖度、植被最小高度、植被最大高度、物种丰富度、香农-维纳多样性指数、植被高度变异系数及样方植物含水量, 以及LAI、植被平均高度和植被覆盖度三者的交互作用项, 建立逐步回归模型。通过逐步回归筛选的最优模型对地上生物量的预测精度可达到91%, 模型的RMSE = 35.60 g·m-2 (图4A), 最优模型如下:
两模型的相对重要性分析结果表明, LAI、植被覆盖度和植被平均高度是影响地上生物量的主要调控因子(图4C、4D)。逐步回归模型中, 各变量及其变量间的交互作用共同解释了地上生物量变异的91%, 其中单个变量贡献了模型全解释度的90% (图4A、4C)。
除植被覆盖度外, 逐步回归模型表明LAI、植被平均高度、植被最大高度和物种丰富度4个关键参数对地上生物量影响较大(图4C)。以往研究表明, LAI与草地地上生物量显著正相关(Wang et al., 2019); 在植被覆盖度的基础上加入植被高度这一变量后, 草地地上生物量预测模型拟合R2从43%上升至68%(Liang et al., 2016)。在本研究中, LAI、植被高度以及物种丰富度的加入, 同样使得模型对地上生物量的预测度提升, 其解释度由84%上升到91% (图3, 图4)。本研究进一步发现, 与植被最小高度和植被最大高度相比, 植被平均高度对地上生物量的预测效果更好(图4C、4D)。植被覆盖度表征植物群落的水平二维结构(Jacquemoud et al., 2009), 结合LAI和植被高度的信息, 能较好地表征植被冠层的三维特征, 准确指示草地样方的地上生物量状况。由LAI、植被覆盖度、植被平均高度、植被最大高度和物种丰富度构筑的逐步回归模型, 可以克服单一变量模型不够稳定、容易造成较大误差的缺点, 估算精度提高。在本研究中, 与应用广泛的机器学习模型相比, 逐步回归模型表现出更好的预测能力(图4A、4B), 原因可能是多元线性模型比机器学习模型更加适合样本量较少的回归分析(Abrougui et al., 2019)。
本文的其它图/表
|