生态学着重于研究生物与生物、生物与环境之间的关系, 在探讨这些关系的过程中, 统计学方法起着非常重要的作用。不同的统计学方法有时会产生完全不同的结果, 这在很大程度上影响了人们对生态学问题的正确认识(Grace, 2006)。因此, 选择合适的数据分析手段至关重要。随着研究的深入, 研究人员发现单变量统计方法在生态学中的广泛应用已开始限制生态学的发展, 因为它难以全面表征自然系统的复杂性, 无法提供所研究系统的完整信息(Grace, 2006)。自然生态系统本质上是复杂的, 由多个相互作用的过程组成的(Clark, 2007; Miao et al., 2009), 而多变量统计方法为解决此类问题提供了一个合适的途径。结构方程模型(structural equation model, SEM)作为一种多变量统计方法, 虽然只是近年才逐渐为生态学家所认识和应用, 但已显示出好的发展势头, 为生态学中很多复杂问题的解决提供了独特的视角, 加深了研究人员对所涉科学问题的认识和理解(Shipley, 2000; Grace, 2006; Shipley et al., 2006; Lamb et al., 2009)。
1 什么是SEM
1.1 SEM定义
对于单变量方程
如果有足够的证据表明变量x可以解释变量y, 即x和y之间具有因果关系或者依赖关系, 那么方程(1)就被称为结构方程(structural equation)。其中参数λ表征x对y的解释强度。由此可见, 一元线性回归方程和单变量方差分析模型均为结构方程。
由两个或两个以上的结构方程组合而成的表示变量间相互关系的联立方程组即为结构方程模型(SEM):
方程(2)-(4)虽然给出了不同变量之间的数量关系, 但是从数学上无法判断哪个变量是“因”, 哪个变量是“果”, 因为A = B与B = A在数学上是没有差别的。因此, SEM从一开始就是以图形来表示的。方程(2)-(4)可以转换为如下的图形模型(图1):
图1
图1
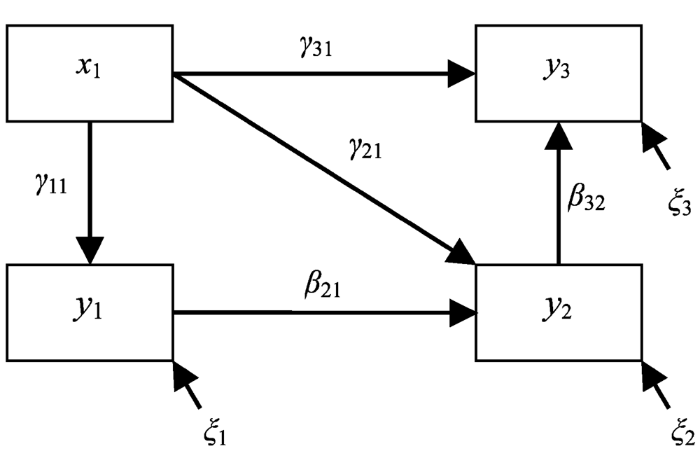
结构方程模型的图形表示形式, 涉及1个自变量(x1)和3个因变量(y1, y2和y3)。其中γ (γ11, γ21和γ31)表示的是变量x对变量y的影响, β (β21和β32)表示的是变量y之间的影响, ξ表示响应变量的残差(改自Grace, 2006)。
Fig. 1
The generic graph demonstration of structural equation model, which involves one independent variable (x1) and three dependent variables (y1, y2 and y3). γ (γ11, γ21 and γ31) represent the effects of x variable on y variables, and β (β21 and β32) represent the effects among y variables. The residual variances are denoted by ξ (Modified from Grace, 2006).
图1中的箭头明确表示了变量之间的因果关系。这里的y1和y2既是反应变量, 也是预测变量。与单变量统计方法注重单个过程不同, SEM将所有相关过程作为一个整体和系统来加以考虑, 一个过程的“果”可能是另外一个过程的“因” (x1→y1→y2, x1→y2→y3)。
1.2 SEM的发展历史
现代SEM的历史最早可追溯到Wright (1918, 1920, 1921)有关路径分析的工作。通过路径分析得到路径系数, 研究人员可以对系统内各种关系进行分解并揭示这些关系背后的潜在机理, 探讨不同因子对同一过程直接与间接的影响, 判别不同因子的相对重要性等。传统的生物统计学、计量经济学、心理测验学和社会计量学等均对SEM的发展起着重要的作用。该阶段的路径分析被称为Wrightian路径分析(采用最小二乘法进行参数估计) (Wright, 1918, 1920, 1921), 以便区别于Jöreskog (1973)的现代路径分析(采用最大似然估计法进行参数估计和对总体模型进行拟合分析)。但是, 路径分析只是现代SEM中的一部分, 它与因子分析的融合才真正是现在SEM的开端(Jöreskog, 1973)。Jöreskog (1973)综合现代路径分析与因子分析开发出著名的LISREL模型和对应的LISREL软件。LISREL模型和软件的出现促进了SEM在社会科学、管理科学、行为科学和生物科学等领域的推广和应用, 以致一段时间内LISREL成为现代SEM的代名词。Grace(2006)认为, 现代SEM实际上包含了如下几个部分的内容: 回归、因子分析、统计建模、模型评价和相关软件等。由此可见, 现代SEM已不单单是指某个或某些统计分析方法, 而是包括了从模型构建、模型评价/选择到实现上述过程的软件开发等多个方面。
1.3 SEM的优势
Fornell (1982)将生态学家相对熟悉的多变量统计方法, 如主成分分析(principle component analysis, PCA)和聚类分析(cluster analysis, CA)等称为 “第一代”多变量统计法, 而将SEM称为“第二代”多变量统计法。总体而言, 二者存在3个重要区别: 1) “第一代”统计法主要是描述性的, 侧重探索性的研究, “第二代”着重于确证性的检验; 2)传统多变量统计法在模型的估计上缺少灵活性; 3) SEM能够同时分析系统内多个变量间的因果关系, 并明确给出各关系的强度大小(Fornell, 1982)。上述区别也正是SEM的优势所在。Grace (2006)综合分析了SEM与其他多变量统计方法, 给出了二者具体的异同对比(表1)。由表1可知, SEM所能解决问题的范围和能力比常见多变量统计方法增大和提高了很多。大部分情况下, SEM能够很好地处理表中各传统多变量统计方法所能处理的问题。换言之, 很多单变量和多变量统计方法都是SEM的特例, 但这并不妨碍研究人员针对某些特定问题采用非SEM方法进行数据分析。
表1 结构方程模型与其他多变量统计方法的比较(改自Grace, 2006)
Table 1
| SEM | DA | RT | PCA | MR | |
|---|---|---|---|---|---|
| 包含判断模型拟合程度的测量 Includes measures of absolute model fit | √ | ||||
| 预先假定变量间因果关系 User can specify majority of relationships | √ | ||||
| 包含隐变量 Includes latent variables | √ | √ | |||
| 处理测量误差 Address measurement error | √ | ||||
| 进行模型整体评价 Allows evaluation of alternative models | √ | √ | |||
| 探讨系统内多个变量间关系 Examines networks of relationships | √ | ||||
| 模型构建 Model building | √ | √ | √ | √ | √ |
DA, 判别分析; MR, 多元回归(多元回归不是多变量统计法, 但是其可以指示变量间的关系); PCA, 主成分分析; RT, 回归树; SEM, 结构方程模型。
DA, discriminant analysis; MR, multiple regression (Though MR itself is not a multivariate method, it could demonstrate the relationships among variables); PCA, principal components analysis; RT, regression tree; SEM, structural equation model.
2 SEM的变量类型
2.1 因果关系
SEM的核心内容之一就是同时探讨系统内变量间的“因果”关系强弱。由于“因果”关系这一术语在历史上存在着很大的争议, 尤其是对于自然科学家和哲学家而言(Wright, 1921; Bollen, 1989; Shipley, 2000), 因此在SEM中有些研究人员倾向于用变量间的“依赖”关系来代替“因果”关系。在SEM的图形框架中, 这种“依赖”关系通常用单向箭头( 
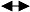
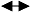
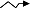
图2
图2
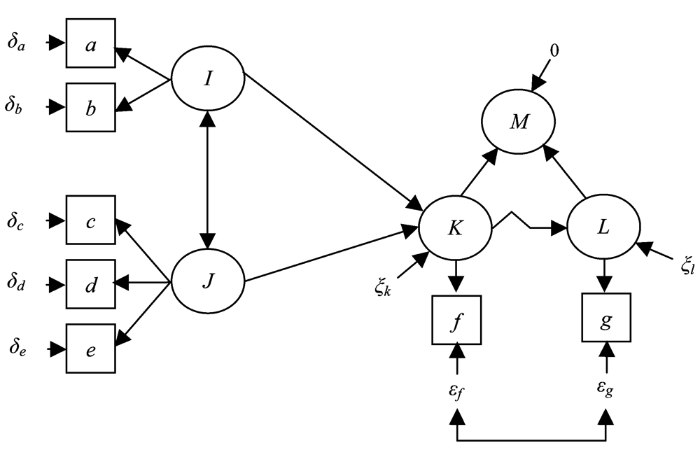
结构方程模型中不同箭头类型和不同变量类型图示。a-g, 观察变量; I-L, 隐变量; M, 综合变量。ξ项表示隐变量上无法明确来源的效应, 而δ和ε表示观察变量上无法明确来源的效应。(改自Grace, 2006)
Fig. 2
The generic demonstration for the types of arrows and variables used in structural equation model. a-g: observed variables; I-L: latent variables; M: composite variable. The ξ terms refer to variables that represent unspecified effects on dependent latent variables, while δ and ε are variables that represent unspecified effects on observed variables. (Modified from Grace, 2006)
2.2 观察变量
观察变量是指在观察或试验过程中能够直接测量的变量, 比如植株高度。在SEM中, 不同水平的试验处理(如施肥梯度)与不同的取样地点等也可以通过观察变量来表示(Grace, 2006)。在SEM的图示中, 一般以方框来代表观察变量。图2中a-g均为观察变量。当只包含此类观察变量时(另加误差变量), SEM又被称为带观察变量的结构方程模型、显变量模型或者路径模型。此处的路径分析不同于Wrightian路径分析。
2.3 误差变量
误差变量是指在数据分析过程中无法被预测变量所解释的那部分效应, 即所谓的残差项。在图形显示中, 误差变量通常不带任何边框, 可以显示在观察变量(包括预测变量与响应变量) (图2中的δa-δe, εf - εg)和隐变量(图2中ξl和ξk)上。在数据分析过程中, 如果不考虑这类因素, 将会对参数估计、模型评价和预测产生重要影响, 以致得到有偏差的结论(Clark, 2007; Dietze et al., 2008)。尤其是针对预测变量, 通常的数据分析假定预测变量是能够通过精确测量得到的, 不存在不确定性, 但在实际应用中, 尤其是在生态学研究中, 这种简化处理将会导致相关统计推断的偏差(Clark, 2007; Dietze et al., 2008), 而SEM明确考虑了预测变量的测量误差问题(表1)。
2.4 隐变量
隐变量是相对显变量或观察变量而言的, 它无法从观察或试验中直接测量到, 但可以通过其他一些可测量的指标估计出来。隐变量通常用以表示某个相对比较抽象的概念, 如不可测量的原因或因子。在SEM的图示中, 以圆形框表示。如图2中, 变量I与J为隐变量, 其中变量I由观察变量a和b指示, J由观察变量c、d和e指示。变量K和L也是隐变量。具体而言, 比如“土壤状况”, 研究者可以通过测量土壤水分含量、养分含量和其他土壤理化指标来指示(Grace et al., 2000; Weiher et al., 2004); 鸟类的“个体大小”, 可以通过测量鸟的个体生物量、翅膀的宽度和喙的长度来指示(Grace, 2006)。路径分析与因子分析(隐变量)的结合使得SEM处理数据的能力大大增强。
2.5 综合变量
综合变量是SEM中另一个表示抽象概念的变量类型。和隐变量的图示表示方式有些相似, 以圆形框表示, 但是增加了一个0干扰项(图2中的变量M)。综合变量反映的是多个显变量或者隐变量的总体影响, 是多个“因”的集合(Blalock, 1964; Heise, 1972; Bollen, 1984)。因此, 综合变量可以分为显变量综合变量和隐变量综合变量, 如图2中的变量M即为隐变量K和L的综合变量。综合变量最早是由Blalock (1964)提出的, Heise (1972)扩展了Blalock的定义, 并明确地给出了几个综合变量适用的事例研究, Bollen (1984)强调在实际数据分析中预先判别显变量综合变量与隐变量综合变量非常重要(图3)。隐变量表示的是不可测量的原因, 需要通过其他一些可测量的变量来指示; 而综合变量代表的是多个原因的集合, 这些原因或者本身是直接可测量的或是通过其他可测量的变量来指示的。在生态学研究中, 综合变量近年才被考虑到SEM里(Grace, 2006)。
图3
图3
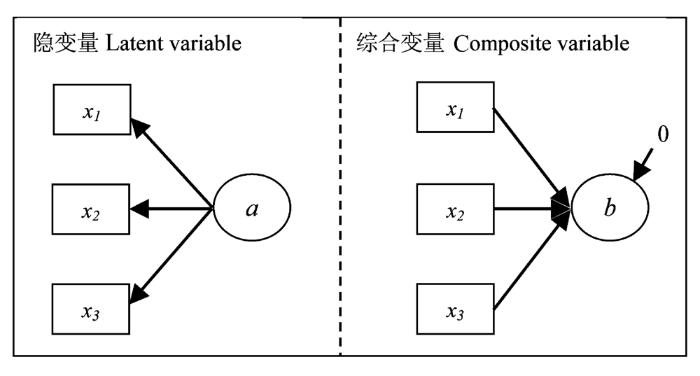
隐变量a与综合变量b的区别。(改自Grace, 2006)
Fig. 3
The difference between latent variable (a) and composite variable (b). (Modified from Grace, 2006)
3 SEM分析的一般步骤
上面介绍了SEM中的一些变量类型, 实际的SEM分析通常将这些变量类型综合于一体。如美国农业部科学家引入跳甲(Aphthona lacertosa和A. nigriscutis)来防除入侵植物乳浆大戟(Euphorbia esula) (Larson & Grace, 2004; Grace, 2006), 就是SEM在生态学中应用的一个比较经典的例子。本文通过这一研究来展示SEM分析的一般步骤, 以帮助不熟悉SEM的研究人员快速理解SEM。影响乳浆大戟种群密度的主要因子是什么?所引入的跳甲能否达到生物控制的目的?为简单起见, 该事例中只涉及观察变量和误差变量, 而未包括相对高级的隐变量和综合变量。
3.1 提出初始模型
如前所述, SEM分析始于对所涉及问题的因果关系假定, 也就是所谓的“初始模型”或“先验模型”。在这个初始模型中, 研究者基于现有的知识水平(如前期的试验研究或观察、其他类似研究等)预先假定变量之间的因果或相关关系。在乳浆大戟的例子中, 研究人员对它有如下几个方面的初步认识:
a)在某一年内, 跳甲的种群密度是与乳浆大戟的密度协同变化的, 因为后者是前者的食物来源(图4中因此假定了路径a和b)。b)甲虫的密度在邻近年份内是相关的, 这主要是源自种群扩散等原因(图4中因此假定了路径c和d)。c)跳甲对食物乳浆大戟的滞后依赖效应, 因为跳甲成熟之前一段时间内是以幼虫的形式来进食乳浆大戟的(图4中因此假定了路径e和f)。d)不同跳甲物种之间可能存在着相互作用, 如对共同食物资源的竞争(图4中因此假定了路径g和h)。e)生物控制的一个基本假定就是认为跳甲会减少乳浆大戟的种群密度(图4中的路径i和j), 同时前一年跳甲的种群密度可能会影响随后一年乳浆大戟的密度(图4中的路径k和l); f)由于存在密度依赖效应, 乳浆大戟的种群密度在邻近年份内应该是相关的(图4中路径m)。
图4
图4
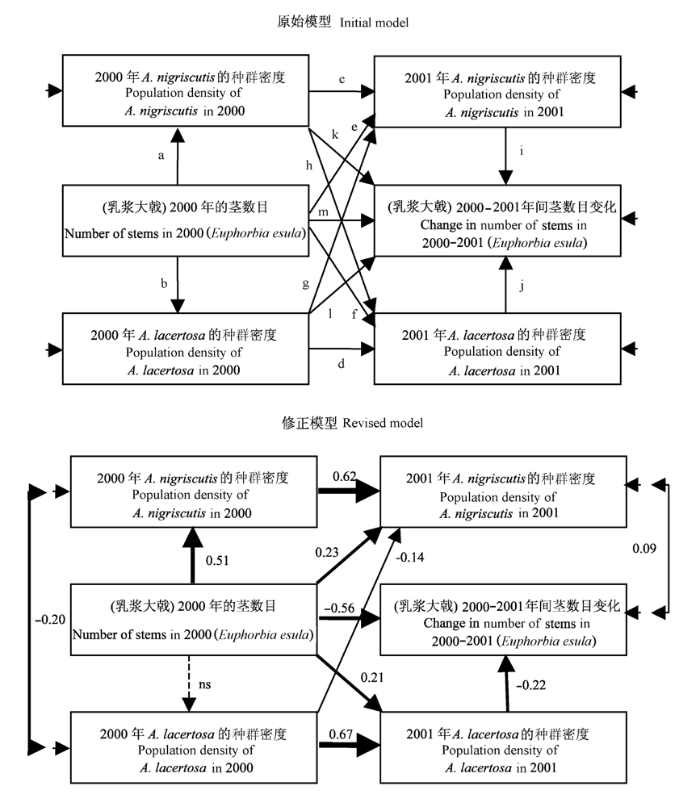
两种跳甲防治乳浆大戟入侵的事例研究。上图为初始模型, 下图为修正后的模型。(改自Larson & Grace, 2004)
Fig. 4
The bio-control of two flea beetle species (Aphthona lacertosa and A. nigriscutis) on invasive species leafy spurge (Euphorbia esula). The upper panel is for the initial model and the lower for the revised model. (Modified from Larson & Grace, 2004)
基于这些认识, 得到了图4的初始模型。该模型是随后所有数据分析的基础, 一个合适的富有生物学意义的初始模型对于问题的认识和理解是非常重要的。提出初始模型后, 需要通过观察或试验取得相关数据来验证该模型的合理性。研究人员从1999年开始进行了为期3年的观察, 为了简单起见, 在本例中仅给出了2000-2001年的结果。
3.2 模型评价
利用观察或试验数据对初始模型进行整体拟合是SEM分析最为核心的内容。SEM既可以对模型整体进行拟合评价, 也可以观察模型中每条路径的相关统计信息(如路径系数是否具有统计学上的意义)。在SEM中最常见的指示模型拟合程度的指标是χ2检验, 因为用于现代SEM参数估计的方法主要为最大似然估计, 而最大似然的拟合函数正好满足χ2分布。所以通常依据与χ2相关的p值可以对初始模型拟合的能力做出判断, 当p > 0.05时, 一般认为该初始模型是可以接受的。此外还有其他一些指标可用来进行模型评价和选择, 如基于信息理论的AIC (Akaike, 1974)和BIC (Raftery, 1993)等, 不同的指标所适用的模型类型可能不同(如嵌套模型与非嵌套模型)。
具体到上面的入侵控制研究中, 通过χ2检验发现, 所收集的数据不能很好地拟合初始模型。修正指数(modification indices, 一些SEM软件程序的输出, 指示初始模型可能缺少了哪些路径)显示应在初始模型中添加物种A. lacertosa和A. nigriscutis种群密度在2000年的负相关关系路径。虽然SEM的评价和修正指数的应用可以显示缺少了哪些路径, 但不能指示研究者在初始模型中哪些路径是多余的, 是否删除某路径需要结合整体模型的拟合状况、各路径的p值与研究者对问题的认知水平。基于这些考虑, 研究者删除了路径k、l和h。删除这些路径后, 整体模型的χ2值变化很小, 意味着这些路径不能代表数据里所包含的信息。尽管2000年乳浆大戟的种群密度对A. lacertosa的种群密度影响不显著(路径b), 但是在修正模型中该路径依然保留下来, 主要是因为已有很多研究表明前者确实能够影响后者。 虽然路径i的系数不具有统计学意义, 但是当删除该路径后发现, A. nigriscutis在2001年的种群密度与年际间乳浆大戟的种群密度变化的残差间存在着正相关关系, 故在修正模型中添加了1个误差项。
3.3 基于修正模型进行推断和预测
经过3.2中的修改, 修正后的模型能很好地拟合观测数据(图4)。从修正后的模型中可以得到如下的结果:
a)物种A. nigriscutis的种群密度受乳浆大戟的种群密度影响较大(路径系数值为0.51), 但A. lacertosa受其影响很小(在本例中差异不显著)。b)两种跳甲的种群密度在2000年是负相关的(-0.20), 对此有3种可能的解释: 两物种的最适生境类型不同、两物种在当初引入时投放地不同、两物种间存在负相互作用, 当前还没足够的信息做出明确的判断。c)两种跳甲的种群密度呈现出时间上的连续性(路径系数分别为0.62和0.67)。d)两种跳甲在2001年的种群密度受2000年乳浆大戟种群密度的影响(路径系数为0.23和0.21)。e) Aphthona lacertosa在2000年的种群密度降低了物种A. nigriscutis在2001年的密度(路径系数为-0.14)。f)乳浆大戟年际间的种群密度变化受A. lacertosa的负影响(路径系数为-0.22), 但A. lacertosa并无此负效应, 意味着这两类跳甲可能在控制乳浆大戟的作用方面存在差异。g)影响乳浆大戟种群密度的最重要因子是它前一年的密度水平(路径系数为-0.56), 即密度依赖起着主要作用。
由此可见, 影响入侵物种乳浆大戟的最主要因素来自于自身的密度依赖效应, 所引入的两类跳甲中A. lacertosa的控制作用更为明显。这个结果与通过单个线性回归所得的结果是不同的: 线性回归显示两类跳甲的种群密度均与乳浆大戟的种群密度成显著的负相关关系(p < 0.05), 即两类跳甲的控制作用均很明显(Larson & Grace, 2004)。在SEM中, 综合多个因素于一体进行分析之后, 研究人员得到了新的认识。
4 SEM在生态学中的应用
近年来, 生态学家逐渐开始应用SEM分析数据。Shipley于2000年出版了第一本介绍生物学家如何应用SEM的著作Cause and Correlation in Biology; 随着技术的发展和SEM在生态学领域应用范围的扩大, Grace于2006年出版了Structural Equation Modeling and Natural Systems, 专门介绍SEM在自然系统中的应用; 在2009年Miao等主编的Real World Ecology: Large-scale and Long-term Case Studies and Methods中, 独辟一章讨论SEM在现实世界生态学(real-world ecology)研究中的作用。
SEM能够为研究人员提供更丰富和全面的信息。比如在生物多样性-生产力关系研究中, 已有大量理论分析和试验控制研究表明, 在特定环境下物种多样性通过生态位互补机制可以提高群落的生产力, 但不清楚在成熟的自然生态系统中是否也是如此。Grace等(2007)收集了12个自然草地生态系统的数据, 综合生物多样性、生产力、外界环境条件和干扰, 利用SEM探讨了4者之间的关系, 发现在自然成熟系统中, 小尺度上的多样性对生产力的影响很弱, 并未发现多样性对生产力正效应的证据(Grace et al., 2007)。还有很多其他的生态学研究事例(Grace, 1999, 2001; Grace et al., 2000; Iriondo et al., 2003; Laughlin et al., 2007; Lamb & Cahill, 2008; Cherry et al., 2009; Saura-Mas et al., 2009; Spitale et al., 2009; Jonsson & Wardle, 2010)表明SEM的应用为研究者提供了认识问题的新视角和解决问题的新能力。
5 相关软件介绍
当前有很多软件可以进行SEM分析, 如LISREL (Jöreskog, 1973)、Mplus (Muthén & Muthén, 2004)和Amos (Byrne, 2001)等, 尤其是由Jöreskog (1973)开发的LISREL软件更是公认的最专业的SEM分析工具。这些软件在数据分析能力上各有侧重、各有千秋, 但均为收费软件。随着免费的R语言的兴起, Fox (2006)开发出针对SEM分析的软件包sem, 其中内置了Graphviz以便生成SEM的图形表示形式, 而且sem软件包处于不断更新之中。随着sem软件包趋于成熟, 选用R语言进行SEM分析应该是将来的一个发展趋势。
6 展望
生态学家所关注的自然系统本质上是复杂的。统计分析的目的就是要从复杂的现象中探讨变量间的直接和间接的关系。不仅要探讨整个系统的净效果, 而且更应注重系统内不同过程间的相互作用。过去生态学的发展侧重于发现普适性的规律, 这仍然是未来生态学发展的一个重要方向。但在全球变化的大背景下, 研究人员越来越注重生物复杂性(biocomplexity)的研究, 如气候变暖和生物入侵对自然系统的影响等。不再只侧重于某个过程, 而是综合多个过程于一体, 同时分析多个过程的影响因子和变化趋势(Grace, 2006; Clark, 2007; Miao et al., 2009)。实际上, 这与自然系统自身的变化是吻合的, 譬如温度升高影响的不只是某个特定的过程, 而是系统内所有相关过程, 区别在于不同过程所受影响的程度可能不同。
随着多组比较(multi-group comparison)与多水平模型(multi-level model)等方法的相继引入(Grace, 2006), SEM所能解决的问题越来越多, 功能也越来越强大, 尤其是与贝叶斯统计的融合更加拓宽了它的应用范围, 形成了一个新的分支, 即贝叶斯结构方程模型(Raftery, 1993; Lee, 2007)。到目前为止, 相比于其他常规统计方法, 采用SEM分析生态学数据的研究还相对较少, 我们期望本文的简略介绍能够为相关研究人员提供一个直观的认识, 增加SEM在生态学中的应用, 从而提高对所研究系统的认识和理解, 并促进现实世界生态学的发展(Miao et al., 2009)。
致谢
兰州大学交叉学科青年创新研究基金(LZUJC200915)、兰州大学中央高校基本科研业务费专项资金(lzujbky-2009-88, lzujbky-2010-49)和国家自然科学基金(31000199, 40721061)资助项目。
参考文献
A new look at the statistical model identification
Multiple indicators: internal consistency or no necessary relationship
Structural Equation Modeling with AMOS
Elevated CO2 enhances biological contributions to elevation change in coastal wetlands by offsetting stressors associated with sea-level rise
Capturing diversity and interspecific variability in allometries: a hierarchical approach
Structural equation modeling with the sem package in R
The factors controlling species density in herbaceous plant communities: an assessment
The roles of community biomass and species pools in the regulation of plant diversity
Factors associated with plant species richness in a coastal tall-grass prairie
Does species diversity limit productivity in natural grassland communities?
Theoretical analyses and experimental studies of synthesized assemblages indicate that under particular circumstances species diversity can enhance community productivity through niche complementarity. It remains unclear whether this process has important effects in mature natural ecosystems where competitive feedbacks and complex environmental influences affect diversity-productivity relationships. In this study, we evaluated diversity-productivity relationships while statistically controlling for environmental influences in 12 natural grassland ecosystems. Because diversity-productivity relationships are conspicuously nonlinear, we developed a nonlinear structural equation modeling (SEM) methodology to separate the effects of diversity on productivity from the effects of productivity on diversity. Meta-analysis was used to summarize the SEM findings across studies. While competitive effects were readily detected, enhancement of production by diversity was not. These results suggest that the influence of small-scale diversity on productivity in mature natural systems is a weak force, both in absolute terms and relative to the effects of other controls on productivity.
Employing nominal variables, induced variables, and block variables in path analysis
Structural equation modelling: an alternative for assessing causal relationships in threatened plant populations
A general method for estimating a linear structural equation system
In: Goldberger AS, Duncan OD eds.
Structural equation modelling reveals plant-community drivers of carbon storage in boreal forest ecosystems
Boreal forest ecosystems are important drivers of the global carbon (C) cycle by acting as both sinks and sources of atmospheric CO(2). While several factors have been proposed as determining the ability of boreal forest to function as C sinks, little is known about their relative importance. In this study, we applied structural equation modelling to a previously published dataset involving 30 boreal-forested islands that vary greatly in their historic fire regime, in order to explore the simultaneous influence of several factors believed to be important in influencing above-ground, below-ground and total ecosystem C accumulation. We found that wildfire was a major driver of ecosystem C sequestration, and exerted direct effects on below-ground C storage (presumably through humus combustion) and indirect effects on both above-ground and below-ground C storage through altering plant-community composition. By contrast, plant diversity influenced only below-ground C storage (and even then only weakly), while net primary productivity and decomposition had no detectable effect. Our results suggest that while boreal forests have great potential for storing significant amounts of C, traits of dominant plant species that promote below-ground C accumulation and the absence of wildfire are the most important drivers of C sequestration in these ecosystems.
When competition does not matter: grassland diversity and community composition
We examined whether the intense root competition in a rough fescue grassland plant community in central Alberta, Canada, was important in structuring plant species diversity or community composition. We measured competition intensity across gradients of species richness, evenness, and community composition, using pairs of naturally occurring plants of 12 species. One plant in each pair was isolated from neighbors to measure competition; community structure and environmental conditions were also measured at each pair. We used structural equation modeling to examine how competition influenced community structure. Competition intensity was unrelated to species richness and community composition, but increased competition intensity was associated with a slight decline in evenness. Size-symmetric root competition was probably unimportant in structuring this plant community because there are no feedback mechanisms through which size-symmetric competition can magnify small initial differences and eventually lead to competitive exclusion. In plant communities with little shoot competition, competition and community structure should be unlinked regardless of competition intensity. In more productive systems, we propose that interactions between root and shoot competition may indirectly structure communities by altering the overall asymmetry of competition.
Shoot, but not root, competition reduces community diversity in experimental mesocosms
Temporal dynamics of leafy spurge (Euphorbia esula) and two species of flea beetles (Aphthona spp.) used as biological control agents
Species richness and soil properties in Pinus ponderosa forests: a structural equation modelling analysis
Structural Equation Modeling: A Bayesian Approach
Real World Ecology: Large-scale and Long-term Case Studies and Methods
Mplus User’s Guide 3rd edn
Bayesian model selection in structural equation models
In: Bollen KA, Long JS eds.
Relationship between post-fire regeneration and leaf economics spectrum in Mediterranean woody species
Fundamental trade-offs generating the worldwide leaf economics spectrum
Recent work has identified a worldwide
Structural equation modelling detects unexpected differences between bryophyte and vascular plant richness along multiple environmental gradients
Multivariate control of plant species richness in a blackland prairie
The relative importance of heredity and environment in determining the piebald pattern of guinea pigs