植物群落生物多样性中性理论自Hubbell (2001)提出以来, 与生态位理论的论战已持续了10年之久, 二者的分歧主要集中在控制群落物种分布格局的生态学过程上。生态位理论认为群落中物种只有产生生态位分化才能共存, 而中性理论认为中性漂变和扩散限制是决定群落物种组成的主要机制。因此, 如何确定中性过程和生态位过程在群落构建中的相对重要性是生态学面临的重要挑战。物种多度分布作为描述生态群落多样性的最基本工具(Borda-de-Água et al., 2011), 能够反映群落构建过程中潜在的普遍原则, 因而被广泛用于检验有关群落结构和生物多样性决定因素的各种假说(Green & Plotkin, 2007; Morlon et al., 2009)。随着物种多度分布格局研究的发展, 用数学方法结合生态学意义建立物种-多度分布模型来模拟多度格局的时空变化成为目前多度格局研究的重要内容(Tokeshi, 1993)。现有理论模型可大致划分为生物多样性中性理论模型、生物统计学模型以及生态位模型三大类, 不同类型的模型体现了群落中不同生态学过程对物种分布的影响(唐志尧等, 2009)。这些理论模型为检验实际数据提供了良好的平台(McGill et al., 2007), 同时已成为现阶段采用实际生态群落观察数据验证中性理论的重要工具(Brown et al., 2011)。
生态学过程的时间动态是解释物种多度格局的重要方面(马克明, 2003)。在森林演替进程中生态学过程的相对重要性发生变化, 以前在群落中占据主导作用的生态过程可能不再重要(张春雨, 2009), 群落物种多度分布格局必然受到影响。因此, 系统研究不同演替阶段森林群落物种多度分布格局动态是十分重要的。格局和过程对物种多度分布的影响还会随取样尺度而变化(Levin, 1992)。群落生境异质性、β多样性、个体聚集程度及自相关性随着取样尺度增加会相应增大(McGill et al., 2007)。 McGill (2003)指出, 随着尺度增加物种多度分布逐渐向对数左偏(log left skew)趋势变化, 并认为这可能是由空间自相关导致的。Borda-de-Água等(2011)研究了巴拿马巴洛科罗拉多岛(Barro Colorado Island, BCI) 50 hm2样地乔木和灌木物种多度分布, 发现当取样面积从1 hm2增加到50 hm2时, 物种多度等级分布从单调递减变为单峰曲线。程佳佳等(2011)对古田山植物群落不同尺度下物种多度分布格局进行拟合, 研究发现不同尺度上适合物种-多度曲线的模型不同, 并且随着取样尺度增加, 中性过程成为决定物种-多度曲线格局的主要生态学过程。因此, 在研究物种多度格局变化时应高度重视取样尺度效应。
目前, 群落物种多度格局研究主要针对特定群落(张金屯, 1999; 刘金福和洪伟, 2001; 郭逍宇等, 2007)或特定环境梯度下的植物群落物种多度分布(冯云等, 2007, 2011)。有关取样尺度和演替阶段对物种多度分布影响的研究还很少(任萍等, 2009; 程佳佳等, 2011)。本文以长白山针阔混交林不同演替阶段森林群落(次生杨桦林(secondary Populus davidiana-Betula platyhylla forest)、次生针阔混交林(secondary conifer and broad-leaved mixed forest)、椴树红松林(Tilia amurensis-Pinus koraiensis mixed forest))为研究对象, 采用中性模型、对数正态分布模型、Zipf模型、分割线段模型和生态位优先模型, 分析了不同尺度下植物种-多度分布格局, 试图阐述长白山针阔混交林群落演替进程中多度格局形成的生态学过程, 旨在为温带森林生物多样性维持机制研究提供数据支撑。
1 材料和方法
1.1 研究区概况
原始阔叶红松林是长白山西区森林的顶级群落类型, 林龄超过200年, 曾是我国重要木材产地之一。但是在20世纪初, 大规模工业采伐使原始阔叶红松林遭到了严重破坏, 大面积森林逐渐为次生林或人工林所代替(张春雨, 2009)。本研究地点位于吉林省白河林业局光明林场(次生杨桦林、次生针阔混交林样地)和长白山北坡自然保护区(椴树红松林样地), 属于受季风影响的温带大陆性山地气候; 年平均气温3.6 ℃, 最热月7月平均气温19.6 ℃, 最冷月1月平均气温-15.4 ℃, 极端最高气温32.3 ℃, 极端最低气温-37.6 ℃; 年降水量707 mm; 土壤类型为山地暗棕色森林土, 土层厚度为20-100 cm (程伯容等, 1981)。
1.2 样地设置
2005-2007年, 在长白山地区典型次生杨桦林、次生针阔混交林和椴树红松林内分别建立5.2 hm2 (260 m × 200 m)固定监测样地, 3块样地构成了一个由次生林逐渐向顶级植被类型过渡的典型演替系列, 样地概况如表1所示(张春雨等, 2009)。每个样地分别划分成130个20 m × 20 m的样方, 清查样方内所有胸径(DBH) ≥ 1 cm的木本植物。调查内容包括每株植物的种类、胸径和坐标等, 并挂牌标记。
表1 长白山永久监测样地概况(张春雨等, 2009)
Table 1
| 林型 Forest type | 经纬度 Longitude and latitude | 平均海拔 Average elevation | 样地面积 Plot area | 原始植被 Primary vegetation |
|---|---|---|---|---|
| 次生杨桦林 Secondary Populus davidiana-Betula platyphylla forest | 42º19.162′ N | 899 m | 5.2 hm2 | 阔叶红松林 Broad-leaved Pinus koraiensis forest |
| 128º07.82′ E | (260 m × 200 m) | |||
| 次生针阔混交林 Secondary conifer and broad-leaved mixed forest | 42º20.91′ N | 748 m | 5.2 hm2 | |
| 128º07.99′ E | (260 m × 200 m) | |||
| 椴树红松林 Tilia amurensis-Pinus koraiensis mixed forest | 42º13.68′ N | 1 042 m | 5.2 hm2 | |
| 128º04.57′ E | (260 m × 200 m) |
1.3 样地树种组成
在次生杨桦林样地中, 共监测到木本植物32种, 隶属于13科21属, 重要值前5位的树种分别为紫椴(Tilia amurensis)、簇毛槭(Acer barbinerve)、山杨(Populus daviana)、色木槭(Acer mono)和白桦(Betula platyphylla); 次生针阔混交林样地中共监测到木本植物31种, 隶属于12科20属, 重要值前5位的树种分别为紫椴、臭松(Abies nephrolepis)、假色槭(Acer pseudo-sieboldianum)、色木槭和白桦; 椴树红松林样地中共监测到木本植物20种, 隶属于11科13属, 重要值前5位的树种分别为红松(Pinus koraiensis)、簇毛槭、紫椴、大青杨(Populus ussuriensis)和臭松(张春雨等, 2009)。
1.4 取样方法
本文采用随机抽样的方法获得取样样方。具体方法为: 在260 m × 200 m样地内随机选择一个点, 以该点作为起始点向x轴、y轴各延伸10 m, 获得10 m × 10 m取样尺度的亚样方。同理, 获得30 m × 30 m、60 m × 60 m和90 m × 90 m取样尺度的亚样方。若所取样方超出260 m × 200 m样地边缘, 则重新取样。每个取样尺度分别抽取500个样方作为重复, 统计500个小样方内DBH ≥ 1 cm 的木本植物物种多度, 之后按多度水平从高到低排序。多度最高的物种水平为1, 多度第二的物种水平为2, 依此类推。最后将每个水平物种多度均值作为该取样尺度下最终物种多度值。以物种多度水平从高到低顺序作为横轴, 以对每个水平物种多度作10为底的对数转换得到的相对物种多度作为纵轴, 最后得到相应取样尺度下的物种-多度曲线。
2 本研究选用的物种多度分布模型
2.1 中性理论模型(neutral theory model, NT)
Hubbell (2001)提出的群落生态学中性理论中有两个基本假设: (1)个体水平的生态等价性, 即群落中处于同一营养级的所有个体在生态学上是等价的, 它们具有相同的出生/死亡、迁入/迁出率; (2)群落饱和性, 即群落的大小保持不变, 一个个体的死亡或迁出必然伴随着另一个个体的出生或迁入。由此, 群落中性理论得出两个重要推论: (1)群落物种多度分布符合零和多项式分布(zero-sum multinomial distribution); (2)扩散限制对群落结构起着决定作用。群落动态实际上是在随机作用下的随机生态漂变过程。大小为J的群落中, S个物种的多度分别为n1, …, ns的概率(Etienne, 2005)为:
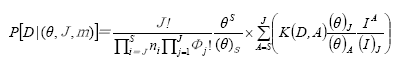
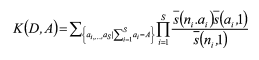
式中, θ为基本多样性指数(fundamental diversity number), 是群落丰富度指标, θ值越大, 群落内物种越丰富; m为迁移率; J为群落总个体数; Φ为具有j个个体的物种数; D为物种多度分布, 包含了局域群落中所有物种的多度, 若群落中共包含S个物种, 则D = (n1, n2,…, ns), ns为第S个物种的多度; I为迁移至局域群落的个体数; ai为物种i的亲代个体数, 则群落内所有物种亲代的个体数为A; K(D, A)为多项式系数。
2.2 生物统计模型
对数正态分布模型(log-normal model, LN)。由Preston (1948)提出, 认为物种个体数的对数形式符合正态分布。μ和σ分别表示正态分布的均值和方差, Φ表示正态偏差, 则第i个种的多度为:
2.3 生态位模型
Zipf模型(Zipf mode, ZM)。Frontier (1985)最先引用此类模型分析了生态学数据, 该模型最早应用于语言学和社会经济学领域(马克明, 2003), 应用于植物群落时, 假定一个种的存在是依赖于以前的物理条件和已存在的物种(彭少麟等, 2003)。先锋种付出较低的代价, 要求很少的条件; 后期演替种要付出较高的代价才能侵入:
式中, Ni表示模型预测的第i个种的多度, N为群落总个体数, q为拟合的最丰富物种多度所占比例, γ为常数, 表示物种出现的平均可能性。
分割线段模型(broken stick model, BS)。由MacArthur (1957)提出, 是一种资源分配模型。假设群落中的资源总量是等于1的线段, 在线段上随机设置S-1个点, 把线段分成S段, 每一部分的长度表述一个种的“多度”。N为群落总个体数, 则第i个种的多度为:
生态位优先模型(niche preemption model, NP)。由Motomur (1932)提出, 假设第一个物种先占用群落中生态位的比例为α份; 第二个物种占用剩余部分的α份, 即α(1-α); 第三个物种再占用剩下的α份, 即α(1-α)2, 依此类推。第i个种的多度为:
3 数据分析方法
3.1 数据处理
本文中所有统计分析与模型拟合均采用国际通用软件R-2.14.1 (R Development Core Team, 2008)完成。其中, 中性模型参数及其理论值是根据实测多度分布数据, 利用极大似然估计法估算出基本多样性指数θ和迁移率m (Etienne, 2005), 然后将所得参数用中性模拟对各群落内物种多度分布进行600次模拟, 对模拟的600次物种多度分布求平均值作为最优预测值(Walker & Cyr, 2007)。其他模型的拟合过程是根据Wilson (1991)提出的方法估算出各自模型的有关参数, 进而求出相应的理论预测分布。
3.2 模型拟合效果检验
3.2.1 拟合优度检验
仅用单一的方法难以充分说明模型的拟合优度, 本文选用χ2检验和K-S检验, 从0.01和0.05两个显著性水平比较两种检验的显著性概率(p), 以确定是否接受相应的模型。若p < 0.01或p < 0.05, 则表示该模型被拒绝; 若p > 0.05, 则表示该模型被接受。
3.2.2 AIC准则
赤池信息量准则(Akaike Information Criterion, AIC)是统计模型选择中广泛应用的标准, 它是由日本学者赤池次弘(Akaike)提出的, 假设模型的误差服从独立正态分布, AIC (Burnham & Anderson, 2002)可表示为:
式中, k表示模型中参数的数量, n表示观察数, RSS表示残差平方和。AIC值越小, 拟合效果越好。
3.2.3 置信区间检验
为进一步检验中性模型的拟合效果, 将中性模型对各个多度水平模拟的600次多度值按大小排序后, 取第15个和第585个分别作为95%置信区间的上下限(Walker & Cyr, 2007)。
4 研究结果
4.1 次生杨桦林物种多度分布
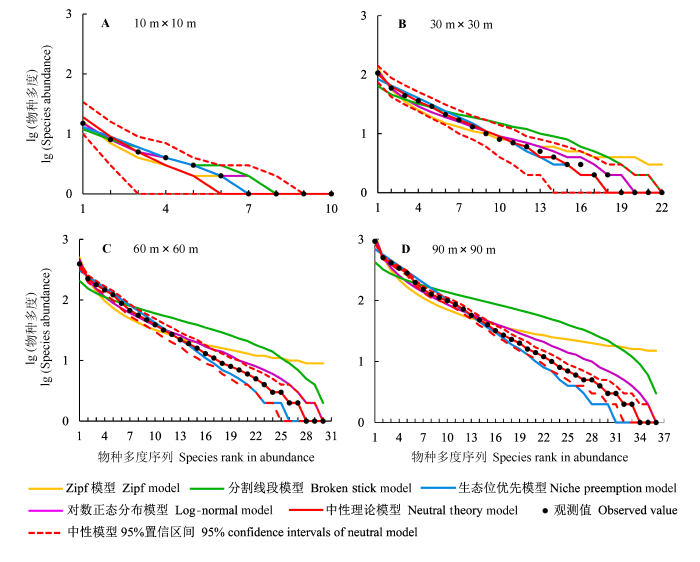
次生杨桦林群落物种多度分布模型拟合如图1所示。在不同取样尺度下, 实际物种多度分布曲线均落入中性模型的95%置信区间内, 且与最优中性预测曲线相吻合。尤其在60 m × 60 m和90 m × 90 m取样尺度下, 最优中性模型拟合曲线与实际多度分布曲线重合。在10 m × 10 m取样尺度上, 中性模型、统计模型和生态位模型的拟合曲线均与实际物种多度分布曲线吻合良好, 其中Zifp模型拟合的中间种多度略小于实际值。在30 m × 30 m、60 m × 60 m和90 m × 90 m取样尺度下, 分割线段模型对丰富种多度的预测值小于实际值, 而对中间种和稀有种多度的预测明显大于实际值; 对数正态模型、Zipf模型和生态位优先模型预测的丰富种多度与实际值接近。
图1
图1
不同取样尺度下次生杨桦林的物种多度分布及模型拟合。
Fig. 1
Species-abundance distribution and model fittings at different sampling scales in secondary Populus davidiana-Betula platyphylla forest.
中性模型的基础多样性指数θ随取样尺度增加而增大, 迁移率m则逐渐减小(表2)。尽管10 m × 10 m取样尺度下所有模型均在χ2检验和K-S检验的可接受范围内, 但根据AIC值大小来看, 对数正态模型是次生杨桦林植物群落在该尺度上的最佳拟合模型。在30 m × 30 m尺度上, χ2检验结果显示分割线段模型的拟合结果与实际物种多度分布差异极显著(p < 0.01), 尽管中性模型、对数正态分布模型、Zipf模型和生态位优先模型都能拟合该尺度下群落物种多度分布, 但中性模型的AIC值最小, 表明其拟合效果最好。在60 m × 60 m、90 m × 90 m尺度上, 只有中性模型能够同时被χ2检验和K-S检验所接受, 其他模型均被χ2检验拒绝。因此, 中性模型能够在不同取样尺度上拟合次生杨桦林群落的物种多度分布。
表2 不同取样尺度下次生杨桦林5种模型拟合的优度检验和中性模型参数
Table 2
| 取样尺度 Sampling scale | θ | m | 检验方法 Test method | NT | LN | ZM | BS | NP |
|---|---|---|---|---|---|---|---|---|
| 10 m × 10 m | 3.90 | 0.05 | AIC | 12.33 | -12.09 | -1.11 | 2.62 | -1.57 |
| D | 0.30 | 0.10 | 0.10 | 0.10 | 0.10 | |||
| χ2 | 2.79 | 0.50 | 1.79 | 1.75 | 0.59 | |||
| 30 m × 30 m | 4.94 | 0.01 | AIC | 19.25 | 57.29 | 85.65 | 102.48 | 75.24 |
| D | 0.09 | 0.09 | 0.27 | 0.23 | 0.05 | |||
| χ2 | 2.62 | 7.39 | 32.22 | 62.71** | 11.14 | |||
| 60 m × 60 m | 5.16 | 1.66×10-3 | AIC | -56.45 | 173.78 | 201.38 | 223.02 | 173.69 |
| D | 0.03 | 0.10 | 0.40* | 0.30 | 0.10 | |||
| χ2 | 0.04 | 58.47** | 199.78** | 437.61** | 47.24* | |||
| 90 m × 90 m | 5.45 | 7.46×10-4 | AIC | -100.05 | 266.41 | 297.52 | 332.30 | 274.31 |
| D | 0.03 | 0.14 | 0.44** | 0.33* | 0.11 | |||
| χ2 | 0.00 | 169.44** | 537.44** | 1473.27** | 152.41** |
NT, LN, ZM, BS and NP stand for neutral model, log-normal model, Zipf model, broken stick model and niche preemption model, respectively. θ and m are parameters of neutral theory model. **, p < 0.01; *, p < 0.05. AIC, Akaike Information Criterion; D, statistic of K-S test.
NT、LN、ZM、BS和NP分别表示中性理论模型、对数正态分布模型、Zifp模型、分割线段模型和生态位优先模型。θ、m为中性模型参数。**, p < 0.01; *, p < 0.05。AIC, 赤池信息准则; D, K-S检验统计量。
4.2 次生针阔混交林物种多度分布
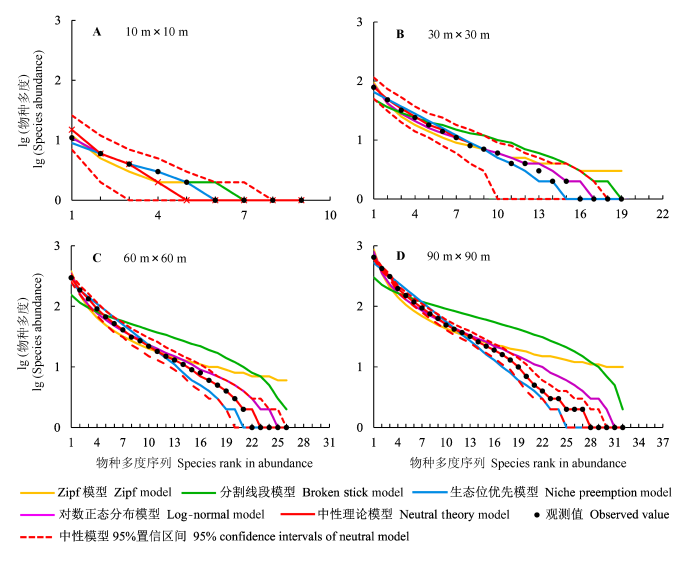
次生针阔混交林不同尺度下物种多度分布的中性模型、生态位模型和生物统计模型的拟合结果如图2所示。不同尺度下实际观察的物种多度分布曲线均落入中性模型95%置信区间内, 且与最优中性预测结果吻合良好。10 m × 10 m尺度上, 5种模型的拟合曲线都与实际物种多度曲线大致吻合, Zipf模型预测的中间种多度略小于实际值。随着尺度增加, 分割线段模型对丰富种多度的预测小于实际值, 而对中间种和稀有种多度的预测明显多于实际值。在30 m × 30 m尺度上, 中性模型、对数正态分布模型、Zipf模型和生态位优先模型预测的物种多度分布均与实际分布吻合较好。在60 m × 60 m和90 m × 90 m尺度上, 对数正态分布模型和Zipf模型预测的中间种和稀有种多度偏大, 而生态位优先模型对中间种和稀有种多度的预测则偏小, 中性模型拟合曲线与实际观察曲线基本重合。
图2
图2
不同取样尺度下次生针阔混交林的物种多度分布及模型拟合。
Fig. 2
Species-abundance distribution and model fittings at different sampling scales in secondary conifer and broad-leaved mixed forest.
次生针阔混交林群落在不同尺度下, 中性模型、生态位模型和生物统计模型拟合优度检验结果见表3。当取样尺度为10 m × 10 m时, 所有模型的预测结果与实际物种多度分布均无显著差异(p > 0.05), 其中对数正态分布模型的AIC值最小, 分割线段模型次之, 表明对数正态分布模型的拟合效果优于分割线段模型。在30 m × 30 m尺度上只有分割线段模型被χ2检验拒绝(p < 0.01), 中性模型、对数正态分布模型、Zipf模型和生态位优先模型能够较好地描述该尺度下次生针阔混交林群落的物种多度分布。根据各模型的AIC值可知, 拟合优度依次为: 中性模型>对数正态分布模型>生态位优先模型。当取样尺度为60 m × 60 m时, 虽然5种模型均能被K-S检验所接受, 但只有中性模型和对数正态分布模型能够被χ2检验接受(p > 0.05), 中性模型的AIC值更小, 拟合效果更好。当取样尺度增加到90 m × 90 m时, 中性模型的AIC值最小, 且不被χ2检验和K-S检验拒绝。对数正态分布模型、Zipf模型、分割线段模型和生态位优先模型的拟合结果均与实际观察值之间存在极显著差异(p < 0.01), 不适合描述该尺度下次生针阔混交林群落物种多度分布。因此, 中性模型能够在不同取样尺度上拟合次生针阔混交林群落的物种多度分布。
图3
图3
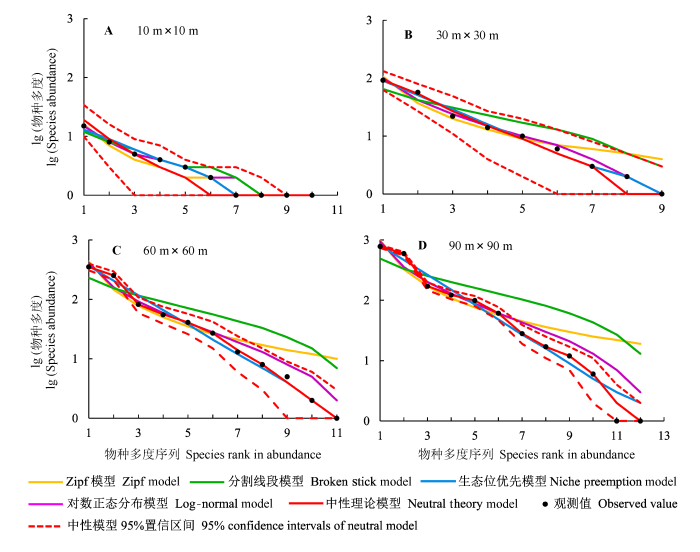
不同取样尺度下椴树红松林的物种多度分布及模型拟合。
Fig. 3
Species-abundance distribution and model fittings at different sampling scales in Tilia amurensis-Pinus koraiensis mixed forest.
表3 次生针阔混交林不同尺度下5种模型拟合优度检验和中性模型参数
Table 3
| 取样尺度 Sampling scale | θ | m | 检验方法 Testing method | NT | LN | ZM | BS | NP |
|---|---|---|---|---|---|---|---|---|
| 10 m × 10 m | 4.02 | 6.81×10-2 | AIC | 11.63 | -9.54 | -1.29 | -3.65 | -3.29 |
| D | 0.33 | 0.11 | 0.11 | 0.11 | 0.11 | |||
| χ2 | 2.57 | 0.50 | 1.62 | 0.94 | 0.44 | |||
| 30 m × 30 m | 4.52 | 8.48×10-3 | AIC | -0.49 | 43.63 | 63.96 | 78.09 | 49.46 |
| D | 0.11 | 0.05 | 0.32 | 0.21 | 0.05 | |||
| χ2 | 2.40 | 4.51 | 18.27 | 39.93** | 6.77 | |||
| 60 m × 60 m | 4.72 | 2.26×10-3 | AIC | -30.12 | 138.20 | 160.07 | 183.85 | 135.34 |
| D | 0.04 | 0.12 | 0.35 | 0.27 | 0.08 | |||
| χ2 | 0.69 | 30.73 | 104.53** | 333.23** | 38.10* | |||
| 90 m × 90 m | 5.13 | 1.08×10-3 | AIC | -62.54 | 228.97 | 250.67 | 278.79 | 211.49 |
| D | 0.03 | 0.16 | 0.41* | 0.31 | 0.09 | |||
| χ2 | 0.03 | 110.80** | 313.97** | 1 083.38** | 89.22** |
NT, LN, ZM, BS and NP stand for neutral model, log-normal model, Zipf model, broken stick model and niche preemption model, respectively. θ and m are parameters of neutral theory model. **, p < 0.01; *, p < 0.05. AIC, Akaike Information Criterion; D, statistic of K-S test.
NT、LN、ZM、BS和NP分别表示中性理论模型、对数正态分布模型、Zifp模型、分割线段模型和生态位优先模型。θ、m为中性模型参数。**, p < 0.01; *, p < 0.05。AIC, 赤池信息准则; D, K-S检验统计量。
4.3 椴树红松林物种多度分布
椴树红松林群落物种多度分布模型拟合如图3所示。实际观测的物种多度曲线都落入中性模型的95%置信区间内。10 m ×10 m尺度上, 对数正态分布模型和生态位优先模型的拟合曲线与实际多度曲线吻合良好; 分割线段模型预测的中间种多度偏大; 中性模型预测的中间种和稀有种多度偏小。在30 m × 30 m尺度上, 分割线段模型预测的丰富种多度偏小, 中间种和稀有种多度偏大; Zipf模型预测的稀有种多度偏大; 中性模型预测的稀有种多度偏小; 对数正态分布模型和生态位优先模型拟合的多度曲线与实际曲线吻合良好。在60 m × 60 m尺度上, 中性模型与生态位优先模型的拟合结果与实际值接近; 而分割线段模型、对数正态分布模型和Zipf模型预测的稀有种多度偏大。在90 m × 90 m尺度上, 生态位优先模型和中性模型预测的稀有种多度略偏大; 对数正态分布模型、分割线段模型和Zipf模型预测的中间种和稀有种多度偏大。
椴树红松林群落各模型的拟合优度检验结果如表4。5种模型在各个尺度上都能被K-S检验所接受。当尺度为10 m × 10 m时, 所有模型的拟合结果都在χ2检验可接受的范围内。由AIC值可知, 该尺度下对数正态分布模型的拟合效果最好, 其次是生态位优先模型、分割线段模型、Zipf模型和中性理论模型。30 m × 30 m尺度上, 分割线段模型和Zipf模型被χ2检验拒绝(p < 0.05); 中性模型的AIC值小于生态位优先模型和对数正态分布模型, 表明中性模型是该尺度上的最佳拟合模型。60 m × 60 m和90 m × 90 m尺度时, 中性模型的AIC值最小, 且预测的物种多度分布与实际观察值之间差异不显著, 其他模型均被χ2检验拒绝(p < 0.05)。因此, 中性模型能够在不同取样尺度上拟合椴树红松林群落的物种多度分布。
表4 椴树红松林不同尺度下5种模型拟合优度检验和中性模型参数
Table 4
| 取样尺度 Sampling scale | θ | m | 检验方法 Testing method | NT | LN | ZM | BS | NP |
|---|---|---|---|---|---|---|---|---|
| 10 m × 10 m | 1.70 | 3.85×10-2 | AIC | 10.93 | - | -0.58 | -4.58 | -6.05 |
| D | 0.11 | 0.11 | 0.33 | 0.22 | 0.11 | |||
| χ2 | 5.40 | 0.00 | 0.55 | 0.68 | 0.18 | |||
| 30 m × 30 m | 1.77 | 4.29×10-3 | AIC | 17.42 | 35.94 | 42.24 | 48.50 | 24.92 |
| D | 0.11 | 0.11 | 0.33 | 0.22 | 0.11 | |||
| χ2 | 2.48 | 6.79 | 18.74* | 36.49** | 2.97 | |||
| 60 m × 60 m | 1.68 | 1.00×10-3 | AIC | -7.13 | 81.56 | 85.51 | 87.36 | 66.07 |
| D | 0.09 | 0.09 | 0.36 | 0.36 | 0.09 | |||
| χ2 | 0.34 | 72.00** | 124.70** | 250.62** | 25.79** | |||
| 90 m × 90 m | 1.62 | 4.28×10-4 | AIC | -6.51 | 110.29 | 113.89 | 115.97 | 94.99 |
| D | 0.08 | 0.17 | 0.42 | 0.33 | 0.17 | |||
| χ2 | 0.52 | 219.31** | 348.21** | 708.79** | 84.41** |
NT, LN, ZM, BS and NP stand for neutral model, log-normal model, Zipf model, broken stick model and niche preemption model, respectively. θ and m are parameters of neutral theory model. **, p < 0.01; *, p < 0.05. AIC, Akaike Information Criterion; D, statistic of K-S test.
NT、LN、ZM、BS和NP分别表示中性理论模型、对数正态分布模型、Zifp模型、分割线段模型和生态位优先模型。θ、m为中性模型参数。**, p < 0.01; *, p < 0.05。AIC, 赤池信息准则; D, K-S检验统计量。
5 讨论
采用代表不同生态学过程的模型来拟合群落物种多度分布, 虽然能够描述群落物种多度的组织结构, 但不足以充分揭示其形成机制, 因为相同的格局可能是由不同的生态学过程导致, 而这些过程并非是相互排斥的。因此, 通过实证研究来揭示不同生态学过程对产生和维持群落物种多度分布格局的相对贡献是十分必要的(Volkov et al., 2005)。程佳佳等(2011)对古田山亚热带常绿阔叶林24 hm2样地物种多度分布格局的研究表明: 中性模型、生态位模型和生物统计模型均适合描述该地区小尺度下(10 m × 10 m)的物种多度分布格局, 但生态位过程的贡献更大; 在中等尺度下(60 m × 60 m和80 m × 80 m)代表中性过程的中性模型和代表生态位过程的Zipf-Mandelbrot模型都适合描述该尺度下的群落物种多度分布格局; 当尺度增大到100 m × 100 m时, 只有中性模型能够很好地预测群落物种多度分布, 这与本文部分研究结果一致。尽管如此, 程佳佳等(2011)并不认为该地区植物群落的组织机制也是中性的。与其结果不同的是, 本研究中在中等尺度下(60 m × 60 m)只有中性模型不被χ2检验拒绝。可能是因为本研究所在样地地形平坦, 生境异质性程度低, 生境过滤作用较弱, 加之曾受到采伐、清林等干扰, 使得非优势物种的可利用资源增加, 从而使中性过程在中等尺度上占据主导地位。而古田山样地地形复杂, 生境异质性随尺度增大而增大, 生境对物种的过滤作用增强, 使得优势种数量增加, 因而生态位过程发挥了更重要的作用。
除亚热带森林外, 温带森林物种多度分布如何随着取样尺度变化也是生态学家长期关注的问题(Zillio & He, 2010)。不同研究尺度上维持物种多度格局的生态学过程也不尽相同。Laliberté等(2009) 、Gazol和Ibáñez (2010)以及Yuan等(2011)认为小尺度上随机过程在温带森林群落构建中具有普遍意义。但是Hao等(2007)和Zhang等(2009)认为长白山阔叶红松林群落在小尺度上存在着强烈的种间竞争, 而且由土壤因子导致的生境异质性是形成非随机过程的重要因素。本研究表明长白山温带次生杨桦林、次生针阔混交林和椴树红松林中, 小尺度上(10 m × 10 m)中性过程和生态位过程均能解释群落物种多度分布, 但生态位过程的解释能力相对较大。可能是由于除了种间竞争和生境异质性, 小尺度上的密度制约效应也是影响群落物种组成的重要原因(黄建雄等, 2010)。而当密度制约对每个物种的作用效应相同时, 可以将群落看作是中性的(Hubbell, 2008)。因此, 小尺度上生态位过程和随机过程对物种多度分布都具有十分重要的作用。
中等研究尺度上(30 m × 30 m、60 m × 60 m), 有些生态位和生物统计模型的拟合结果与实际观测数据没有显著差异, 但其拟合效果均不如中性模型。这表明在中等尺度上中性过程开始逐渐取代生态位过程成为维持物种多度分布的主要机制。Laliberté等(2009)、Gazol和Ibáñez (2010)及Yuan等(2011)研究表明, 大尺度上生境异质性通常是决定群落组成的主要因素, 而本文研究结果显示在大尺度上(90 m × 90 m), 仅有中性模型能够用来拟合次生杨桦林、次生针阔混交林和椴树红松林群落的物种多度分布, 其余模型均被拒绝。可能是因为大尺度上生境异质性主要由地形差异引起, 本文中次生杨桦林、次生针阔混交林和椴树红松林样地地形平坦, 生境异质性相对较小, 由生境异质性导致的物种生态位分化减弱; 同时, 随着尺度增大物种迁移率降低, 扩散限制对群落物种组成的影响增强, 群落逐渐被中性的过程所驱动(Stokes & Archer, 2010)。这与Wang等(2008)和Zhang等(2010)的研究结果一致, 他们认为在长白山森林群落构建过程中, 生境异质性并不是最重要的因素。因此, 大尺度上中性过程维持物种多度分布所表现出的重要作用并未否定生态位过程的作用。
长白山温带针阔混交林群落不同发育阶段林分的物种组成、群落结构存在较大差异, 维持物种共存的生态学过程也不同。通常演替初期群落种间竞争作用激烈, 种间竞争作用随着演替进程逐渐减弱。本研究显示, 在不同演替阶段, 中性模型能够很好地拟合群落的物种多度分布, 生态位模型和生物统计模型的拟合效果不理想。可能是由于处于演替初期和中期的次生林经历了多次人为采伐和清林干扰, 使得种间竞争作用减弱。因为在生态位理论中, 生境过滤和种间竞争作用是群落构建过程中两个作用方向相反的驱动力(闫帮国等, 2010), 干扰和演替作为生境过滤因素会降低群落内的种间竞争作用, 导致生态位过程对群落物种多度格局的贡献减弱。椴树红松林处于演替顶级阶段, 群落结构复杂、物种组成和数量比例相对稳定, 种间竞争作用并不强烈, 因而生态位过程对群落物种组成的影响并不明显。因此, 中性模型对不同发育阶段群落的物种多度分布均能进行预测。
综上所述, 决定温带森林植物群落物种组成的生态学过程与尺度和演替阶段有关。尽管中性模型能够在不同尺度上拟合长白山不同演替阶段群落物种多度分布, 但并不代表群落的构建机制是随机的。群落结构是否与中性模型预测一致是验证中性理论的必要条件, 却不是充分条件(McGill et al., 2007)。本文虽然证实了中性模型对温带森林物种多度分布预测的有效性, 但不能否认竞争排除、生态位分化和演替进程中生境过滤等作用对群落构建的贡献。因此, 可以认为中性过程是影响温带森林群落构建的重要生态学过程, 但不是唯一过程。这也证实了群落构建过程中中性理论和生态位理论并非相互矛盾, 而是相互融合的。因此, 中性模型能够很好地拟合长白山针阔混交林群落物种多度分布, 并且中性过程与生态位过程共同作用于群落的构建过程(Zhang et al., 2010)。在研究森林群落物种多度分布时, 应高度重视取样尺度和演替阶段的影响, 并采用多种模型进行拟合。
致谢 国家林业公益性行业科研专项项目(200904- 022和201104009)和国家“十二五”科技支撑项目(2012BAC01B03)资助。
参考文献
Spatial scaling of species abundance distributions
Linking ecological processes with spatial and non-spatial patterns in plant communities
Model Selection and Multi-Model Inference: a Practical Information-Theoretic Approach 2nd edn. Springer-Verlag
The main soil groups and their properties of the natural reserve on northern slope of Changbai Mountain
Responses of species-abundance distribution to varying sampling scales in a subtropical broad-leaved forest
A new sampling formula for neutral biodiversity
Effects of slope position on species abundance distribution of Quercus wutaishanica community in Dongling Mountain of Beijing
Species abundance distribution of Quercus liaotungensis forest along altitudinal gradient in Dongling Mountain, Beijing
Variation of plant diversity in a temperate unmanaged forest in northern Spain: behind the environmental and spatial explanation
A statistical theory for sampling species abundances
Species abundance patterns of artificial vegetation in Antaibao open mine
Vertical structure and spatial associations of dominant tree species in an old-growth temperate forest
Influence of environmental factors on phylogenetic structure at multiple spatial scales in an evergreen broad-leaved forest of China
Assessing the scale-specific importance of niches and other spatial processes on beta diversity: a case study from a temperate forest
The problem of pattern and scale in ecology: the Robert H. MacArthur Award Lecture
Study on species abundance distribution of Castanopsis kawakamii natural forest in Fujian Sanming
Advances of the study on species abundance pattern
On the relative abundance of bird species
Does Mother Nature really prefer rare species or are log-left-skewed SADs a sampling artifact?
Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework
Taking species abundance distributions beyond individuals
On the statistical treatment of communities
Advances in research on the species- abundance relationship models in multi-species collection
The commonness, and rarity, of species
Species abundance distribution pattern of forest communities on Loess Plateau
R: A Language and Environment for Statistical Computing
Niche differentiation and neutral theory: an integrated perspective on shrub assemblages in a parkland savanna
Species-area relationship in biological communities
Species abundance patterns and community structure
Density dependence explains tree species abundance and diversity in tropical forest
Testing the standard neutral model of biodiversity in lake communities
Spatial pattern of diversity in an old-growth temperate forest in Northeastern China
Methods for fitting dominance/diversity curves
Plant community assembly rules across a subalpine grazing gradient in western Sichuan, China
Scale specific determinants of tree diversity in an old growth temperate forest in China
Population Structure of Tree Species and Environmental Interpretation in Coniferous and Broadleaved Mixed Forest in Changbai Mountain (长白山针阔混交林种群结构及环境解释)
Partitioning temperate plant community structure at different scales
Community structure in different successional stages in north temperate forests of Changbai Mountains, China
Aims The Changbai Mountains had a large area of undisturbed temperate old-growth forest that was partly destroyed by large-scale industrial logging at the turn of the 20th century and replaced by secondary forests and plantations. Our objective was to further understand ecosystem development, community composition and structure, and spatial distribution of major tree populations. Methods Three long-term 5.2 hm2 forest plots were established in secondary Populus davidiana-Betula platyphylla forest (PBF), secondary conifer and broadleaved mixed forest (SCBMF) and Tilia amurensis-Pinus koraiensis mixed forest (TPMF) in the Changbai Mountains following the protocols of the Center for Tropical Forest Science forest dynamic plot. We tagged and recorded the species, diameter at breast height (DBH), height and crown diameter of all live and dead trees with DBH >1 cm. We determined the spatial distribution of five dominant canopy tree species by pair-correlation g(r) function and performed variation partitioning analysis to estimate the environmental effect on spatial distribution. Important findings We recorded 20 949, 14 725 and 12 062 live individuals and basal areas of 24.74, 32.07 and 56.64 m2·hm–2 in PBF, SCBMF and TPMF, respectively. Tilia amurensis, with the overall highest importance value and basal area, was the major dominant tree species in SCBMF, P. davidiana and B. platyphylla dominated PBF and P. koraiensis dominated TPMF. In the secondary forests BPF and SCBMF, the size-class distribution of Pinus koraiensis, Acer mono, Abies nephrolepis, Picea jezoensis and Tilia amurensis showed the reverse J-shape form, whereas P. koraiensis and T. amurensis showed normal distributions in TPMF. Paired-correlation g(r) function showed that the main tree species had aggregated distributions, and the aggregation intensity decreased with the increasing distances. Environment variables had a strong effect on tree distribution, but the interpretation power of environment variables was very low in TPMF. ]]>
Fine-scale species co-occurrence patterns in an old-growth temperate forest
Species abundance patterns in some broad-leaved deciduous forests in New York, USA
Inferring species abundance distribution across spatial scales