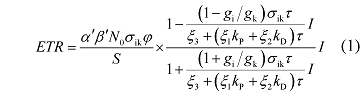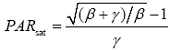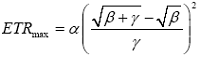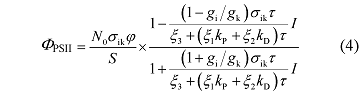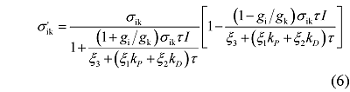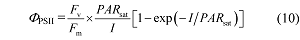光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数。由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency)。因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 )。
按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强。而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光。实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 )。同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少。已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 )。由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因。此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降。 正是由于存在这两个问题, 所以限制了这些模型的 应用。
而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连。首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成。而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 )。此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 )。由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物。
针对以上的3个推测, 在本研究中, 首先, 我们基于光合电子流对光的响应机理模型(Ye et al ., 2013a , 2013b )推导出Φ PSII 对光的响应模型, 确定其变化规律与PSII天线色素分子的内禀特性之间的关系; 其次, 利用Φ PSII 对光响应的机理模型、负指数模型和指数模型分别拟合剑叶金鸡菊(Coreopsis lanceolata )、黄荆(Vitex negundo )和大狼杷草(Bidens frondosa )在正常条件下Φ PSII 对光的响应曲线, 判断所推导的Φ PSII 对光的响应模型是否合理和有效, 并与负指数模型和指数模型的拟合结果进行比较, 以确定这些模型的优缺点; 再次, 用所测量的ETR 对光的响应数据验证我们的推测, 即植物的Φ PSII 随光强的增加而下降可能与其天线色素分子的有效光能吸收截面特性密切相关; 最后, 利用所拟合的结果确定LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI的分配比例为0.5是否适合剑叶金鸡菊、黄荆和大狼杷草。因此, 这些问题的探讨将为研究植物的Φ PSII 对光的响应以及Φ PSII 随光强的增加而下降的机理提供理论基础, 同时也为研究植物的ETR -I 和Φ PSII -I 提供数学工具。
1 材料和方法
1.1 材料
供试材料为自然生长在江西省吉安市井冈山大学校园内的剑叶金鸡菊、黄荆和大狼杷草。
1.2 测定及计算方法
在2013年6月连续的几个晴天内, 在9:00-11:30和14:30-16:30, 随机选5株长势较为一致的健壮植株用LI-6400-40B (LI-COR, Lincoln, USA)测定其ETR 对光的响应曲线和其他参数。在测定过程中, 气室CO2 浓度控制为(390 ± 2) μmol·mol-1 , 气室温度设置为(35 ± 1) ℃, 气室的空气相对湿度设置为50%-70%。光合有效辐射(PAR )设置为2000、1800、1600、1400、1200、1000、800、600、400、200、100、50和0 μmol·m-2 ·s-1 共13个水平, 并分别于各光强下测定剑叶金鸡菊、黄荆和大狼杷草的光合电子流(J )或ETR 和其他参数, 每个测定点的响应时间在120 s以上。然后分别用植物光合电子流对光响应的机理模型、负指数模型和指数模型拟合这3种植物的光合电子流对光的响应曲线, 得到其光响应曲线的初始斜率(α )或光强为0时的最大光化学量子效率(Φ PSIImax )或植物经过暗适应的PSII最大光化学量子产量(F v /F m )、饱和光强(PAR sat )、最大光合电子流(J max )或最大电子传递速率(ETR max ), 并用相关的参数估算天线色素分子的有效光能吸收截面对光的响应曲线等。
1.3 机理模型的推导
植物叶片的天线色素分子吸收的光能将在光化学反应、热耗散和荧光发射等3条途径上竞争分配(Oxborough, 2004 ; Baker, 2008 ), Ye等(2013a, 2013b)在此基础上构建了一个ETR 对光的响应机理模型。其数学表达式为:
式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例。其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 )。
由于在一定的环境下植物叶片天线色素分子的物理参数是确定的, 可以假设: α = α'β 'N 0 φσ ik /S (μmol electrons·(μmol photons)-1 ), β = ((1-g i /g k )σ ik τ )/ (ξ 3 + (ξ 1 k P + ξ 2 k D )τ ) (m2 ·s·(μmol photons)-1 ), γ = ((1+ g i /g k )σ ik τ )/(ξ 3 + (ξ 1 k P + ξ 2 k D )τ ) (m2 ·s·(μmol photons)-1 ), 那么公式(1)可以简化为:
由公式(2)可以得到植物叶片的饱和光强(PAR sat )和最大电子传递速率(ETR max )分别为:
此外, 按照Krall和Edward (1992) 给出的光合电子流对光的响应公式:
ETR = α'β 'Φ PSII I (3)
对比公式(1)和公式(3), 可以得到Φ PSII 与光强之间的关系式为:
由公式(4)可知, Φ PSII 不仅与光强存在非线性关系, 还与天线色素分子的本征光能吸收截面(σ ik )、天线色素分子数(N 0 )、激子的传递效率(φ )、激子处于最低激发态的平均寿命(τ )、光化学反应速率(k P )和热耗散速率(k D )、天线色素分子处于基态i 的简并度(g i )和激发态k 的简并度(g k )等参数存在密切的关系。
假设ω = N 0 φσ ik /S (μmol electrons·(μmol photons)-1 ), 那么公式(4)可以简化为:
这里的ω 是Φ PSII -I 曲线的初始斜率。由公式(5)可知, Φ PSII 随光强的增加而非线性下降。对比公式(2)和公式(5)可知, α /ω = α'β' , 由此也可以确定Dual-PAM- 100所推荐的α' 和β' 的值分别为0.84和0.5是否合理。
由公式(1)还我们还可以得到天线色素分子有效光能吸收截面(σ' ik )与光强之间的关系(Ye et al ., 2013a , 2013b )为:
由公式(6)可知, σ' ik 随光强的增加呈非线性下降。对比公式(6)和公式(4)可知, 对于一定植物在一定环境条件下, Φ PSII 与σ' ik 成正比, 即:
Φ PSII = N 0 φσ' ik /S (7)
1.4 经验模型的介绍
现有拟合Φ PSII -I 曲线的经验模型有负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )、指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛。负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是:
Φ PSII = Φ PSIImax e- kwI
式中的Φ PSIImax 是光强为0时的最大光化学量子效率, k w 是一个常数, I 为光强。与公式(8)相对应的ETR 对光的响应模型的数学表达式为:
ETR = α'β'IΦ PSIImax e- kwI
由公式(9)可以得到植物叶片的饱和光强和最大电子传递速率分别为: PAR sat = 1/k w 和ETR max =α'β'PAR sat Φ PSIImaxe -1 。
指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )的数学表达式是:
式中的PAR sat 、F v /F m 和I 与以上的定义相同。由公式(10)可以直接估算出植物叶片的饱和光强(PAR sat )。与公式(10)相对应的光合电子流对光的响应模型的数学表达式为:
ETR = α'β' (F v /F m ) PAR sat [1-exp(-I /PAR sat )] (11)
此外, 由公式(11)也可以直接估算植物叶片的PAR sat , 最大电子传递速率则为: ETR max = α'β' (F v /F m ) PAR sat [1-exp(-1)]。
1.5 数据处理
ETR-I 曲线和Φ PSII -I 曲线的实验数据处理用SPSS 12.5; 用Origin 7.0作图, 然后用Adobe Illustrator CS5进行图形处理, 采用SPSS 12.5作方差差异显著性分析、ANOVA检验和配对样本t 检验, 用DPS 7.05软件作模型分析。本文将用AIC信息准则并结合确定系数(R 2 )对3个模型的拟合结果进行比较, 并判断3个模型的优缺点。其中AIC的计算参考Akaike (1973)的方法, R 2 则是直接由SPSS 12.5在拟合数据后给出。AIC值越小, 说明拟合的模型既精度高又简洁; R 2 是衡量所建立模型效果好坏的指标之一, 其值越大表明模型拟合得越好。此外, 为了比较α /ω 与0.42 (α'β' = 0.42)之间是否存在显著性差异, 本文对此进行了配对样本t 检验, 显著性水平设定为α = 0.05。文中的图和表中的部分数据均用平均值±标准误差表示。
1.6 叶绿素含量的测定
取测定完光合电子流和净光合速率对光的响应曲线的成熟叶片, 在不同叶片上取直径0.7 cm的叶圆片30片, 分3组, 分别浸入10 mL 80%丙酮的提取液中, 盖紧样品瓶盖并密封, 避光低温放置48 h至叶圆片无色。然后参照Arnon (1949)的方法测量叶绿素的含量, 重复5次取平均值。
2 实验结果和分析
2.1 3种植物叶片的电子传递速率对光的响应曲线(ETR -I 响应曲线)
植物的光合电子流对光的响应曲线一般可以分为3个阶段(Ralph & Gademann, 2005 ): 第一阶段是光合电子流随光强的增加而几乎线性增加; 第二阶段是光合电子流随光强的增加缓慢增加到一个平台; 第三阶段是光合电子流随光强的增加而下降, 出现光PSII的动力学下调(每个光强点的测量时间小于60 s)或光抑制现象(每个光强点的测量时间大于180 s)。由图1 可知, 剑叶金鸡菊和大狼杷草的光合电子流随光强的增加而下降, 而黄荆的光合电子流随光强的增加一直在增加, 尚未出现下降。
图1 剑叶金鸡菊(A)、黄荆(B)和大狼杷草(C)的电子传递速率对光的响应曲线(ETR -I )(平均值±标准误差)。公式(2)为ETR = α (1-β I ) / (1 + γI ) I , 其中α 为ETR -I 的初始斜率, β 为光抑制项, γ 为光饱和项, I 为光强; 公式(9)为ETR =α'β'IΦ PSIImax e- kwI α' 为叶片光能吸收系数, β' 为光能在2个光系统的分配比例, Φ PSIImax 为光强为0时的最大光化学量子效率, k w 是一个常数; 公式(11)为ETR = α'β' (F v /F m ) PAR sat [1-exp (-I /PAR sat )], 其中F v /F m 为光系统II的最大光量子效率, PAR sat 为饱和光强。
Fig. 1 Light-response curves of electron transport rate (ETR - I ) for Coreopsis lanceolata (A), Vitex negundo (B) and Bidens frondosa (C) (mean ± SE ). Equation (2) is ETR =α (1-β I ) / (1 + γI ) I . Here α is the initial slope of ETR -I , β is the photoinhibition term, γ is the saturation term, I is light intensity; Equation (9) is ETR =α'β'IΦ PSIImax e- kwI α' is the light absorption coefficient of leaf, β' is the light energy distribution coefficient between photosystem II and photosystem I, Φ PSIImax is the maximum photochemical quantum efficiency while I = 0, k w is a constant; Equation (11) is ETR = α'β' (F v /F m ) PAR sat [1-exp(-I /PAR sat )]. Here F v /F m is the maximum quantum of photosystem II, PAR sat is the saturation irradiance.
由图1 和表1 可知, 由公式(2)和(9)得到剑叶金鸡菊、黄荆和大狼杷草的最大光合电子流和饱和光强与实测值高度符合, 而由公式(11)得到的ETR max 分别为156.5、155.99和86.67 μmol·m-2 ·s-1 , 测量值则分别约为230.4、228.8和135.8 μmol·m-2 ·s-1 , 估算值分别约为实测值的67.8%、68.2%和63.8%; 由公式(11)得到的PAR sat 分别为617.83、633.1和395.2 μmol·m-2 ·s-1 , 测量值分别约为1600、1750和1400 μmol·m-2 ·s-1 , 估算值尚未达到实测值的一半(表1 )。此外, 由表1 的数据可知, 公式(2)、(9)和(11)拟合3种植物的光合电子流对光的响应曲线的R 2 都在0.994以上。如果用确定系数的大小表示模型的拟合与实际测量曲线的符合度, 那么(2)式的拟合效果最好, (11)式的拟合效果最差。如果以AIC值的大小作为衡量标准, 则以公式(9)的拟合效果最好, 公式(11)的拟合效果最差(表1 )。
2.2 三种植物叶片的PSII实际光化学量子效率对光的响应曲线(Φ PSII -I )
由图2 可知, 3种植物的Φ PSII 随光强的增加而非线性下降, 且剑叶金鸡菊和黄荆的下降速度略有差异, 但大狼杷草的Φ PSII 随光强的增加而下降的速度最快。由图2 还可知, 3个模型都能较好地拟合剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 曲线, R 2 超过0.984。此外, 由表2 的数据可知, 如果仅从R 2 值的大小衡量3个模型的优劣, 那么以机理模型的拟合效果最好, 指数模型最差; 如果以AIC值的大小衡量, 那么以负指数模型的拟合效果最好, 拟合效果最差的是指数模型。
图2 剑叶金鸡菊(A)、黄荆(B)和大狼杷草(C)的实际光量子效率对光的响应曲线(Φ PSII -I )(平均值±标准误差)。公式(5)为Φ PSII = ω (1-βI ) / (1 + γI ), 其中ω 为Φ PSII -I 的初始斜率; 公式(8)为Φ PSII = Φ PSIImax e- kwI Φ PSII = (F v /F m ) PAR sat / I (1-exp(-I /PAR sat ))。β 、γ 、F v /F m 、Φ PSIImax 、k w 和PAR sat 的定义同图1 。
Fig. 2 Light-response curves of Φ PSII for Coreopsis lanceolata (A), Vitex negundo (B) and Bideas frondosa (C)(mean ± SE ). Equation (5) is Φ PSII = ω (1-βI ) / (1 + γI ). Here ω is the initial slope of Φ PSII -I ; Equation (8) is Φ PSII = Φ PSIImax e- kwI Φ PSII = (F v /F m ) PAR sat / I (1-exp(-I /PAR sat )). The definition of β , γ , F v /F m , Φ PSIImax , k w and PAR sat see Fig. 1 .
除了可用公式(9)和(11)拟合ETR -I 曲线分别得到这3种植物的Φ PSIImax 和F v /F m 的值外, 也可以由公式(8)和(10)拟合Φ PSII -I 曲线得到这3种植物的Φ PSIImax 和F v /F m 的值(表2 )。此外, 由公式(11)和(10)分别拟合ETR -I 曲线和Φ PSII -I 曲线得到的PAR sat 有较大的差异。比如, 由公式(11)拟合剑叶金鸡菊的ETR -I 曲线得到的PAR sat 为617.83 μmol·m-2 ·s-1 , 而由公式(10)拟合剑叶金鸡菊的Φ PSII -I 曲线得到的PAR sat 为824.95 μmol·m-2 ·s-1 , 后者是前者的1.33倍。
2.3 3个模型拟合3种植物的Φ PSIImax 、F v /F m 和α /ω 的结果比较
由(8)和(9)式可以估算植物的Φ PSIImax , 由(10)和(11)式可以估算植物的F v /F m , 但对比表1 和表2 中的数据可知, 由(8)和(9)式估算同种植物的Φ PSIImax 得到的值并不相同, 由(10)和(11)式估算同种植物的F v /F m 得到的值也不相同。例如, 用(9)式得到剑叶金鸡菊的Φ PSIImax 为0.859, 而由(8)式得到剑叶金鸡菊的Φ PSIImax 为0.771, 前者是后者的1.114倍。为了确定这些模型估算的Φ PSIImax 之间和F v /F m 之间是否存在差异, 对拟合结果进行了ANOVA检验, 发现用(8)和(9)式分别得到的剑叶金鸡菊和黄荆的Φ PSIImax 值之间存在显著差异(表3 ); 同时也对由(10)和(11)式估算的植物F v /F m 的值进行了ANOVA检验, 发现用(10)和(11)式分别得到的剑叶金鸡菊(和黄荆)的F v /F m 值之间也存在显著差异(表3 )。此外, 由配对样本t 检验得知: 由(2)式和(9)式或(5)式和(8)式得到3种植物的PAR sat 与实测值之间不存在显著差异, 而与(10)或(11)式得到3种植物的PAR sat 与实测值之间则存在显著差异(数据没有给出)。
此外, 对α /ω 和0.42 (α'β' = 0.42)之间进行了配对样本t 检验, 发现剑叶金鸡菊和黄荆的α /ω 和0.42存在显著差异(表3 )。由此可知剑叶金鸡菊、黄荆和大狼杷草的α /ω 值分别为0.455、0.468和0.474, 这3个值都比LI-6400-40B给出α'β' 的推荐值0.42大。
2.4 三种植物天线色素分子的有效光能吸收截面对光的响应曲线(σ' ik -I )
天线色素分子的有效光能吸收截面(σ' ik )表示其在不同光强下天线色素分子捕获光子能力的大小。由图3 可知, 剑叶金鸡菊、黄荆和大狼杷草的天线色素分子有效光能吸收截面随光强的增加而下降, 表明这3种植物随光强的增加其捕获光子的能力都在逐渐变小。由图3 和表1 的数据可知, 剑叶金鸡菊和黄荆天线色素分子在高光强(2000 μmol·m-2 ·s-1 )时, 它们的有效光能吸收截面几乎相同, 约为1.85 × 10-21 m2 , 表明这两种植物在高光强时依然可以吸收较多的光能。而大狼杷草天线色素分子的有效光能吸收截面在高光强(2000 μmol·m-2 ·s-1 )时约为1.02 × 10-21 m2 , 表明在高光强时, 它吸收的光能比剑叶金鸡菊和黄荆少81%左右。
图3 剑叶金鸡菊(A)、黄荆(B)和大狼杷草(C)的有效光能吸收截面对光的响应曲线(σ' ik -I )(平均值±标准误差)。
Fig. 3 Light-response curves of effective light energy absorption cross-section (σ' ik -I ) for Coreopsis lanceolata (A), Vitex negundo (B) and Bidens frondosa (C)(mean ± SE ).
此外, 对比图3 和图2 可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 曲线与它们的σ' ik -I 曲线非常相似。
3 讨论和结论
首先, 基于光合电子流对光响应的机理模型构建了一个Φ PSII 对光的响应模型。由Φ PSII -I 模型可知, Φ PSII 不仅与光强有关, 而且还与植物天线色素的内禀特性存在非线性的关系, 即Φ PSII 的大小除了与叶绿素的含量有关外, 还与天线色素分子的本征光能吸收截面和激子的传递效率等有关。
其次, 指数模型和负指数模型主要用于藻类(Laws et al ., 2002 ; Ritchie, 2008 )、浮游植物(Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少。本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 )。由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符。此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线。如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差。而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值。这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )。由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题。
再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 )。本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似。此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因。然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低。
最后, 用公式(8)和(9)分别得到的剑叶金鸡菊和黄荆的Φ PSIImax 值之间存在显著差异(表3 ); 用公式(10)和(11)估算得到剑叶金鸡菊和黄荆的F v /F m 值之间也存在显著差异(表3 )。此外, 剑叶金鸡菊、黄荆和大狼杷草的α /ω 值分别为0.455、0.468和0.474, 其中剑叶金鸡菊和黄荆α /ω 的值与0.42 (α'β' = 0.42)存在显著差异(表3 ), 也即这3个值都比LI- 6400-40B给出α'β' 的推荐值0.42要大。其原因可能是剑叶金鸡菊、黄荆和大狼杷草叶片的光能吸收系数(β' )要大于0.84或光能分配到PSII的系数要大于0.5, 也即由LI-6400-40B给出α' 和β' 的推荐值不适合这3种植物。如果能用球面积分仪测量植物叶片的光吸收系数(β' ), 就可以由公式(2)和(5)或由公式(8)和(9)计算叶片吸收的光能是否平均地分配到光系统II和光系统I, 即可以确定α' 是否恒等于0.5。这为研究植物光能是否平均分配到光系统II和光系统I提供了一个有效工具。
总之, 本文所构建的Φ PSII -I 模型可以很好地拟合3种植物PSII的实际光化学量子效率对光的响应曲线, 并可以很好地说明Φ PSII 随光强的增加而非线性下降的原因是捕光色素分子的有效光能吸收截面随光强的增加而下降。同时, 其对应的ETR -I 响应模型可以拟合不同植物的电子传递速率对光的响应曲线, 并可以合理地解释植物的PSII动力学下调或光抑制等生理现象。此外, 当Φ PSII -I 模型和ETR-I 机理模型相结合, 并结合球面积分仪测量植物叶片的光吸收系数时, 就可以研究植物叶片吸收的光能是否平均地分配到PSII和PSI。
The authors have declared that no competing interests exist.
作者声明没有竞争性利益冲突.
参考文献
文献选项
[1]
Akaike H 1973 ). A new look at the statistical model identifica- tion
.IEEE Translations Automatic Control , 19 , 716 -723 .
[2]
An DS Cao J Huang XH Zhou J Dou MA 2015 ). Application of Lake-model based indices from chlorophyll fluorescence on sugarcane seedling drought resistance study
.Chinese Journal of Plant Ecology , 39 , 398 -406 . (in Chinese with English abstract)[安东升 , 曹娟 , 黄小华 , 周娟 , 窦美安 (2015 ). 基于Lake模型的叶绿素荧光参数在甘蔗苗期抗旱性研究中的应用
. 植物生态学报 , 39 , 398 -406 .]
[本文引用: 3]
[3]
Arnon DJ 1949 ). Copper enzymes in isolated chloroplasts. Polyphenoloxidase in Beta vulgaris
. Plant Physiology , 24 , 1 -15 .
[4]
Baker NR 2008 ). Chlorophyll fluorescence: A probe of photosynthesis in vivo
. Annual of Review Plant Biology , 59 , 89 -113 .
[本文引用: 4]
[5]
Ehleringer J Pearcy RW 1983 ). Variation in quantum yield for CO2 uptake among C3 and C4 plants
.Plant Physiology , 73 , 555 -559 .
[本文引用: 2]
[6]
Feng HQ Jiao QS Tian WY Sun K Jia LY 2014 ). Effects of extracellular ATP on the characteristics of photochemical reaction in bean (Phaseolus vulgaris) leaves under differ- ent light intensities
. Chinese Journal of Plant Ecology , 38 , 1117 -1123 . (in Chinese with English abstract)[冯汉青 , 焦青松 , 田武英 , 孙坤 , 贾凌云 (2014 ). 不同光强下细胞外三磷酸腺苷对菜豆叶片光化学反应特性的影响
. 植物生态学报 , 38 , 1117 -1123 .]
[本文引用: 2]
[7]
Genty B Briantais JM Baker NR 1989 ). The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence
.Biochimica et Biophysica Acta , 990 , 87 -92 .
[本文引用: 2]
[8]
Goh CH Ko SM Koh S Kim YJ Bae HJ 2012 ). Photosyn- thesis and environments: Photoinhibition and repair mech- anisms in plants
.Journal of Plant Biology , 55 , 93 -101 .
[本文引用: 1]
[9]
Govindjee (2002 ). A role for a light-harvesting antenna complex of photosystem II in photoprotection
.The Plant Cell , 14 , 1663 -1668 .
[本文引用: 2]
[10]
Krall JP Edward GE 1992 ). Relationship between photo- system II activity and CO2 fixation in leaves
.Physiologia Plantarum , 86 ,180 -187 .
[本文引用: 5]
[11]
Laws E Sakshaug E Babin M Dandonneau Y Falkowski P Geider R Legendre L Morel A Sondergaard M Takahashi M Williams PJ 2002 ). Photosynthesis and primary productivity in marine ecosystems: Practical aspects and application of techniques
.Joint Global Ocean Flux Study , 36 , 1 -77 .
[本文引用: 5]
[12]
Lin L Tang Y Zhang JT Yan WL Xiao JH Ding C Dong C Ji ZS 2015 ). Effects of different water potentials on leaf gas exchange and chlorophyll fluorescence parameters of cucumber during post-flowering growth stage
.Chinese Journal of Applied Ecology , 26 , 2030 -2040 . (in Chinese with English abstract)[林琭 , 汤昀 , 张纪涛 , 闫万丽 , 肖建红 , 丁超 , 董川 , 籍增顺 (2015 ). 不同水势对黄瓜花后叶片气体交换及叶绿素荧光参数的影响
. 应用生态学报 , 26 , 2030 -2040 .]
[本文引用: 3]
[13]
Lin MZ Wang ZW He LC Xu K Cheng DL Wang GX 2015 ). Plant photosynthesis-irradiance curve response to pollution show non-competitive inhibited Michaelis kinet- ics
.PLOS ONE , 10 , e0142712 . doi: 10.1371/journal. pone. 0142712 .
[14]
Major KM Dunton KH 2002 ). Variations in light-harvesting characteristics of the seagrass,Thalassia testudinum: Evidence for photoacclimation
. Journal of Experimental Marine Biology and Ecology , 275 , 173 -189 .
[本文引用: 1]
[15]
Murchie EH Ali A Herman T 2015 ). Photoprotection as a trait for rice yield improvement: Status and prospects
.Rice , 8 , 31 -40 .
[本文引用: 1]
[16]
Nelson N Yocum CF 2006 ). Structure of function of photo- systems I and II
.Annual Review of Plant Biology , 57 , 521 -565 .
[本文引用: 1]
[17]
Niyogi KK Truong TB 2013 ). Evolution of flexible non- photochemical quenching mechanisms that regulate light harvesting in oxygenic photosynthesis
.Current Opinion in Plant Biology , 16 , 307 -314 .
[本文引用: 1]
[18]
Oxborough K 2004 ). Imaging of chlorophyll a fluorescence: Theoretical and practical aspects of an emerging technique for the monitoring of photosynthetic performance
.Journal of Experimental Botany , 55 , 1195 -1205 .
[本文引用: 2]
[19]
Panitchayangkoon G Hayes D Fransted KA Caram JR Harel E Wen J Blankenship RE Engel GS 2010 ). Long-lived quantum coherence in photosynthetic complexes at physiological temperature
.Proceedings of the National Academy Sciences of the United States of America , 107 , 12766 -12770 .
[本文引用: 1]
[20]
Ralph PJ Gademann R 2005 ). Rapid light curves: A powerful tool to assess photosynthetic activity
.Aquatic Botany , 82 , 222 -237 .
[本文引用: 2]
[21]
Richter M Renger T Knorr A 2008 ). A Block equation approach to intensity dependent optical spectra of light harvesting complex II. Excitation dependence of light harvesting complex II pump-probe spectra
.Photosynthesis Research , 95 , 119 -127 .
[本文引用: 1]
[22]
Ritchie RJ 2008 ). Fitting light saturation curves measured using modulated fluorometry
.Photosynthesis Research , 96 , 201 -215 .
[本文引用: 9]
[23]
Ritchie RJ Bunthawin S 2010 ). The use of pulse amplitude modulation (PAM) fluorometry to measure photosynthesis in a cam orchid,Dendrobium spp.(D. cv. Viravuth Pink)
. International Journal of Plant Sciences , 171 , 575 -585 .
[本文引用: 8]
[24]
Rochaix JD 2014 ). Regulation and dynamics of the light- harvesting system
. Annual of Review Plant Biology , 65 , 287 -309 .
[本文引用: 1]
[25]
Sarovar M Ishizaki A Fleming G Whaley B 2010 ). Quantum entanglement in photosynthetic light-harvesting com- plexes
.Nature Physics , 6 , 462 -467 .
[本文引用: 1]
[26]
Shi SB Li TC Li M Liu SZ Li AD Ma JP 2015 ). Interaction effect analysis of soil drought and strong light on PSII nonphotochemical quenching inKobresia pygmaea leaves
. Plant Physiology Journal , 51 , 1678 -1686 . (in Chinese with English abstract)[师生波 , 李天才 , 李妙 , 刘世增 , 李爱德 , 马剑平 (2015 ). 土壤干旱和强光对高山嵩草叶片PSII反应中心非光化学猝灭的交互影响分析
. 植物生理学报 , 51 , 1678 -1686 .]
[本文引用: 1]
[27]
Silsbe GM Kromkamp JC 2012 ). Modeling the irradiance dependency of the quantum efficiency of photosynthesis
.Limnology and Oceanography: Methods , 10 , 645 -652 .
[本文引用: 10]
[28]
Smyth TJ Pemberton KL Aiken J Geider RJ 2004 ). A meth- odology to determine primary production and phytoplank- ton photosynthetic parameters from fast repetition rate fluorometry
.Journal of Plankton Research , 26 , 1337 -1350 .
[本文引用: 8]
[29]
Takahashi S Badger MR 2011 ). Photoprotection in plants: A new light on photosystem II damage
.Trends in Plant Sciences , 16 , 53 -59 .
[本文引用: 1]
[30]
Vijayan P Browse J 2002 ). Photoinhibition in mutants of arabidopsis deficient in thylakoid unsaturation
.Plant Physiology , 129 , 876 -885 .
[本文引用: 1]
[31]
Ware MA Belgio E Ruban AV 2015 ). Photoprotective capacity of non-photochemical quenching in plants acclimated to different light intensities
.Photosynthesis Research , 126 , 261 -274 .
[本文引用: 2]
[32]
Webb WL Newton M Starr D 1974 ). Carbon dioxide ex- change of Alnus rubra: A mathematical model
. Oecologia , 17 , 281 -291 .
[本文引用: 3]
[33]
White AJ Critchley C 1999 ). Rapid light curves: A new fluo- rescence method to asses the state of the photosynthetic apparatus
.Photosynthesis Research , 59 , 63 -72 .
[本文引用: 1]
[34]
Ye ZP Hu WH Xiao YA Fan DY Yin JH Duan SH Yan XH He L Zhang SS 2014 ). A mechanistic model of light-response of photosynthetic electron flow and its application
.Chinese Journal of Plant Ecology , 38 , 1241 -1249 . (in Chinese with English abstract)[叶子飘 , 胡文海 , 肖宜安 , 樊大勇 , 尹建华 , 段世华 , 闫小红 , 贺俐 , 张斯斯 (2014 ). 光合电子流对光响应的机理模型及其应用
. 植物生态学报 , 38 , 1241 -1249 .]
[本文引用: 1]
[35]
Ye ZP Robakowski P Suggett DJ 2013 a). A mechanistic model for the light response of photosynthetic electron transport rate based on light harvesting properties of photosynthetic pigment molecules
.Planta , 237 , 837 -847 .
[本文引用: 4]
[36]
Ye ZP Suggett DJ Robakowski P Kang HJ 2013 b). A mechanistic model for the photosynthesis-light response based on the photosynthetic electron transport of PSII in C3 and C4 species
.New Phytologist , 199 , 110 -120 .
[本文引用: 4]
A new look at the statistical model identifica- tion
1973
基于Lake模型的叶绿素荧光参数在甘蔗苗期抗旱性研究中的应用
3
2015
... 光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数.由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency).因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 ). ...
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Copper enzymes in isolated chloroplasts. Polyphenoloxidase in Beta vulgaris
1949
Chlorophyll fluorescence: A probe of photosynthesis in vivo
4
2008
... 光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数.由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency).因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 ). ...
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... 植物叶片的天线色素分子吸收的光能将在光化学反应、热耗散和荧光发射等3条途径上竞争分配(Oxborough, 2004 ; Baker, 2008 ), Ye等(2013a, 2013b)在此基础上构建了一个ETR 对光的响应机理模型.其数学表达式为: ...
Variation in quantum yield for CO2 uptake among C3 and C4 plants
2
1983
... 式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例.其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
... 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
不同光强下细胞外三磷酸腺苷对菜豆叶片光化学反应特性的影响
2
2014
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence
2
1989
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
Photosyn- thesis and environments: Photoinhibition and repair mech- anisms in plants
1
2012
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
A role for a light-harvesting antenna complex of photosystem II in photoprotection
2
2002
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
Relationship between photo- system II activity and CO2 fixation in leaves
5
1992
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例.其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
... ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
... 此外, 按照Krall和Edward (1992) 给出的光合电子流对光的响应公式: ...
Photosynthesis and primary productivity in marine ecosystems: Practical aspects and application of techniques
5
2002
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 其次, 指数模型和负指数模型主要用于藻类(Laws et al ., 2002 ; Ritchie, 2008 )、浮游植物(Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少.本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 ).由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符.此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线.如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差.而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
不同水势对黄瓜花后叶片气体交换及叶绿素荧光参数的影响
3
2015
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Plant photosynthesis-irradiance curve response to pollution show non-competitive inhibited Michaelis kinet- ics
2015
Variations in light-harvesting characteristics of the seagrass,Thalassia testudinum: Evidence for photoacclimation
1
2002
... 式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例.其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
Photoprotection as a trait for rice yield improvement: Status and prospects
1
2015
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Structure of function of photo- systems I and II
1
2006
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
Evolution of flexible non- photochemical quenching mechanisms that regulate light harvesting in oxygenic photosynthesis
1
2013
... 光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数.由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency).因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 ). ...
Imaging of chlorophyll a fluorescence: Theoretical and practical aspects of an emerging technique for the monitoring of photosynthetic performance
2
2004
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... 植物叶片的天线色素分子吸收的光能将在光化学反应、热耗散和荧光发射等3条途径上竞争分配(Oxborough, 2004 ; Baker, 2008 ), Ye等(2013a, 2013b)在此基础上构建了一个ETR 对光的响应机理模型.其数学表达式为: ...
Long-lived quantum coherence in photosynthetic complexes at physiological temperature
1
2010
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
Rapid light curves: A powerful tool to assess photosynthetic activity
2
2005
... 植物的光合电子流对光的响应曲线一般可以分为3个阶段(Ralph & Gademann, 2005 ): 第一阶段是光合电子流随光强的增加而几乎线性增加; 第二阶段是光合电子流随光强的增加缓慢增加到一个平台; 第三阶段是光合电子流随光强的增加而下降, 出现光PSII的动力学下调(每个光强点的测量时间小于60 s)或光抑制现象(每个光强点的测量时间大于180 s).由图1 可知, 剑叶金鸡菊和大狼杷草的光合电子流随光强的增加而下降, 而黄荆的光合电子流随光强的增加一直在增加, 尚未出现下降. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
A Block equation approach to intensity dependent optical spectra of light harvesting complex II. Excitation dependence of light harvesting complex II pump-probe spectra
1
2008
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
Fitting light saturation curves measured using modulated fluorometry
9
2008
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 现有拟合Φ PSII -I 曲线的经验模型有负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )、指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... 其次, 指数模型和负指数模型主要用于藻类(Laws et al ., 2002 ; Ritchie, 2008 )、浮游植物(Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少.本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 ).由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符.此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线.如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差.而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少.本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 ).由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符.此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线.如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差.而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
The use of pulse amplitude modulation (PAM) fluorometry to measure photosynthesis in a cam orchid,Dendrobium spp.(D. cv. Viravuth Pink)
8
2010
... 光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数.由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency).因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 ). ...
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 现有拟合Φ PSII -I 曲线的经验模型有负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )、指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... ; Ritchie et al ., 2010 )的数学表达式是: ...
... 其次, 指数模型和负指数模型主要用于藻类(Laws et al ., 2002 ; Ritchie, 2008 )、浮游植物(Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少.本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 ).由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符.此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线.如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差.而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Regulation and dynamics of the light- harvesting system
1
2014
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Quantum entanglement in photosynthetic light-harvesting com- plexes
1
2010
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
土壤干旱和强光对高山嵩草叶片PSII反应中心非光化学猝灭的交互影响分析
1
2015
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Modeling the irradiance dependency of the quantum efficiency of photosynthesis
10
2012
... 光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数.由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency).因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 ). ...
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 现有拟合Φ PSII -I 曲线的经验模型有负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )、指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... 指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )的数学表达式是: ...
... 其次, 指数模型和负指数模型主要用于藻类(Laws et al ., 2002 ; Ritchie, 2008 )、浮游植物(Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少.本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 ).由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符.此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线.如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差.而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
A meth- odology to determine primary production and phytoplank- ton photosynthetic parameters from fast repetition rate fluorometry
8
2004
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 现有拟合Φ PSII -I 曲线的经验模型有负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )、指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... 指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )的数学表达式是: ...
... 其次, 指数模型和负指数模型主要用于藻类(Laws et al ., 2002 ; Ritchie, 2008 )、浮游植物(Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 用于陆地高等植物较少.本研究中, 我们分别用所构建的Φ PSII 对光响应的机理模型, 同时用负指数模型和指数模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的Φ PSII -I 响应曲线, 发现这3个模型都可以较好地拟合这3种植物的Φ PSII -I 响应曲线, R 2 最低为0.984, 但由指数模型拟合得到这3种植物的PAR sat 与实测值相差较大, 约为实测值的一半甚至更少(表2 ).由配对样本t 检验也可以得知: 由公式(10)或(11)得到3种植物的PAR sat 与实测值之间存在显著差异, 而由公式(3)和(5)或公式(8)和(9)得到3种植物的PAR sat 与实测值之间不存在显著差异(数据并没有给出), 这表明由机理模型和指数模型拟合得到的PAR sat 与实测值相符.此外, 我们用这3个Φ PSII -I 响应模型所对应的ETR -I 响应模型分别拟合了剑叶金鸡菊、黄荆和大狼杷草的ETR -I 响应曲线.如果仅用R 2 来判断3个模型拟合的优劣, 那么以ETR -I 和Φ PSII -I 机理模型为最佳, 指数模型最差; 如果以AIC作为判断标准, 则以负指数模型为最佳, 指数模型为最差.而由图1 、图2 、表1 和表2 的拟合结果可知, 只有ETR -I 的机理模型和负指数ETR -I 的响应模型拟合得到的ETR max 和PAR sat 与实测值高度符合, 而由指数ETR -I 的响应模型得到的ETR max 和PAR sat 远低于实测值.这些研究结果与前人的结果相似(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
... ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ).由此可知, 与机理模型和负指数模型的拟合结果相比, 指数模型不适于研究藻类、浮游植物和陆地植物的Φ PSII -I 响应和ETR -I 响应问题. ...
Photoprotection in plants: A new light on photosystem II damage
1
2011
... 光系统II (PSII)的实际光化学量子效率(Φ PSII )为PSII反应中心部分关闭时的实际原初光能捕获效率, 表征作用光下PSII吸收光能用于原初醌电子受体QA 还原的实际运行效率, 是一个被广泛应用的荧光参数.由于它与通过PSII反应中心的线性电子传递(LET )有直接的联系, 可快速地确定光强变化时或其他环境条件下PSII反应中心的作用效率(Baker, 2008 ), 所以, 它又被称为PSII的运行效率(PSII operating efficiency).因此, 研究它的变化规律具有重要的理论价值和实际意义(Ritchie & Bunthawin, 2010 ; Takahashi & Badger, 2011 ; Silsbe & Kromkamp, 2012 ; Niyogi & Truong, 2013 ; 安东升等, 2015 ). ...
Photoinhibition in mutants of arabidopsis deficient in thylakoid unsaturation
1
2002
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Photoprotective capacity of non-photochemical quenching in plants acclimated to different light intensities
2
2015
... 按照Genty等(1989)关于电子传递速率(ETR )或光合电子流(J )的理论, ETR 的大小可以由公式ETR = α' × β' × Φ PSII × I 得到, 式中的Φ PSII 就是PSII的实际光化学量子效率, α'、β'、I 分别为光能在PSII和PSI的分配系数(无量纲)、叶片的光吸收系数(无量纲)和光强.而Φ PSII = (F′ m - F s )/F′ m (Genty et al ., 1989 ; Krall & Edward, 1992 ), 其中F′ m 为光下的最大荧光, F s 为光下稳态荧光.实验结果表明: Φ PSII 是一个依赖光强的函数, 它随光强的增加而下降(Genty et al ., 1989 ; Krall & Edward, 1992 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; Ware et al ., 2015 ).同时, Φ PSII 也可以由几个经验模型直接拟合(Laws et al ., 2002 ; Smyth et al ., 2004 ; Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ), 但这些经验模型主要应用于藻类和浮游植物(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和少数几种陆生植物(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ), 其他陆生植物应用较少.已有的研究结果表明: 由指数模型分别拟合ETR 对光的响应曲线(ETR-I )和Φ PSII 对光的响应曲线(Φ PSII -I )的响应数据得到相应的饱和光强(PAR sat )和植物经过暗适应的PSII最大光能利用效率F v /F m (F v 为可变荧光, F m 为最大荧光产量)差异较大, 且所估算的饱和光强与实际测量值差异较大(Laws et al ., 2002 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 ); 负指数模型拟合ETR -I 和Φ PSII -I 的响应数据得到的饱和光强与实测值符合, 但由此模型得到光强为0时的最大光化学量子效率(Φ PSIImax )之间存在较大的差异(Ritchie, 2008 ).由此可知, 由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间存在明显差异, 但尚不清楚产生这种现象的原因.此外, 这两个模型也不能解释为什么植物的Φ PSII 会随光强的增加而下降. 正是由于存在这两个问题, 所以限制了这些模型的 应用. ...
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
Carbon dioxide ex- change of Alnus rubra: A mathematical model
3
1974
... 现有拟合Φ PSII -I 曲线的经验模型有负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )、指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... )和正切函数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ), 其中以负指数模型和指数模型应用最为广泛.负指数模型(Ritchie, 2008 ; Ritchie et al ., 2010 )的数学表达式是: ...
... 指数模型(Webb et al ., 1974 ; Smyth et al ., 2004 ; Silsbe & Kromkamp, 2012 )的数学表达式是: ...
Rapid light curves: A new fluo- rescence method to asses the state of the photosynthetic apparatus
1
1999
... 再次, 大量的实验数据表明: Φ PSII 随光强的增加而下降是一个普遍现象(Ritchie, 2008 ; Ritchie & Bunthawin, 2010 ; Silsbe & Kromkamp, 2012 ; 冯汉青等, 2014 ; 安东升等, 2015 ; 林琭等, 2015 ; 师生波等, 2015 ; Ware et al ., 2015 ).本研究中剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 也随光强的增加而下降(图2 ), 与前人的结果相似.此外, 由图1 和图2 可知, 负指数模型和指数模型可以拟合三种植物的ETR -I 和Φ PSII -I 响应曲线, 却不能解释Φ PSII 随光强的增加而下降的原因, 对应的电子传递速率对光的响应模型即公式(9)和(11)也不能解释在ETR -I 响应曲线中出现的光系统II的动力学下调(White & Critchley, 1999 ; Ralph & Gademann, 2008 )或光抑制(Vijayan & Browse, 2002 ; Goh et al ., 2012 ; Rochaix, 2014 ; Murchie et al ., 2015 )的原因.然而由公式(7)Φ PSII 与σ ik ′ 之间的关系可知, 剑叶金鸡菊、黄荆和大狼杷草的Φ PSII 随光强的增加而非线性下降的原因来自它们的天线色素分子的有效光能吸收截面随光强的增加而下降(图3 ), 即天线色素分子吸收光子的能力随光强的增加而减少, 由此3种植物用于光合作用的光能就减少了, 从而导致PSII的实际光化学量子效率降低. ...
光合电子流对光响应的机理模型及其应用
1
2014
... 式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例.其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
A mechanistic model for the light response of photosynthetic electron transport rate based on light harvesting properties of photosynthetic pigment molecules
4
2013
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... 针对以上的3个推测, 在本研究中, 首先, 我们基于光合电子流对光的响应机理模型(Ye et al ., 2013a , 2013b )推导出Φ PSII 对光的响应模型, 确定其变化规律与PSII天线色素分子的内禀特性之间的关系; 其次, 利用Φ PSII 对光响应的机理模型、负指数模型和指数模型分别拟合剑叶金鸡菊(Coreopsis lanceolata )、黄荆(Vitex negundo )和大狼杷草(Bidens frondosa )在正常条件下Φ PSII 对光的响应曲线, 判断所推导的Φ PSII 对光的响应模型是否合理和有效, 并与负指数模型和指数模型的拟合结果进行比较, 以确定这些模型的优缺点; 再次, 用所测量的ETR 对光的响应数据验证我们的推测, 即植物的Φ PSII 随光强的增加而下降可能与其天线色素分子的有效光能吸收截面特性密切相关; 最后, 利用所拟合的结果确定LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI的分配比例为0.5是否适合剑叶金鸡菊、黄荆和大狼杷草.因此, 这些问题的探讨将为研究植物的Φ PSII 对光的响应以及Φ PSII 随光强的增加而下降的机理提供理论基础, 同时也为研究植物的ETR -I 和Φ PSII -I 提供数学工具. ...
... 式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例.其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
... 由公式(1)还我们还可以得到天线色素分子有效光能吸收截面(σ' ik )与光强之间的关系(Ye et al ., 2013a , 2013b )为: ...
b). A mechanistic model for the photosynthesis-light response based on the photosynthetic electron transport of PSII in C3 and C4 species
4
2013
... 而由Φ PSII = (F′ m - F s )/F′ m 的定义可知, Φ PSII 与光合作用原初反应中的PSII的开闭和天线色素分子发射的荧光过程紧密相连.首先, 天线色素分子吸收光能后将由基态跃迁到高能态, 然后这些激发能将分配到光化学反应、热耗散和发射叶绿素荧光这3条主要途径且它们彼此竞争(Oxborough, 2004 ; Baker, 2008 ), 这种分配过程直接影响到随后的光合电子传递与同化力的形成.而原初反应是一个纯粹的物理过程, 涉及天线色素分子的光能吸收、量子态的改变、激子的共振传递和退激发等, 这些过程又是由天线色素分子的内禀特性所决定的(Govindjee, 2002 ; Baker, 2008 ; Richter et al ., 2008 ; Panitchayangkoon et al ., 2010 ; Sarovar et al ., 2010 ).此外, 光合作用也与光合能力的形成(如ATP和NADPH的形成) (Govindjee, 2002 ; Nelson & Yocum, 2006 ; Ye et al ., 2013a , 2013b )和与碳同化相连的酶动力过程有关(Lin et al ., 2015 ).由此推测: (1) Φ PSII 的大小应该与植物的天线色素分子、PSII的内禀特性和酶动力学过程密切相关; (2) Φ PSII 随光强的增加而下降可能与捕光色素分子的有效光能有关; (3)由负指数和指数模型拟合ETR-I 和Φ PSII -I 的响应曲线分别得到的Φ PSIImax 之间和F v /F m 之间明显存在差异可能是由于LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI之间的分配比例为0.5并非适合所有的植物. ...
... 针对以上的3个推测, 在本研究中, 首先, 我们基于光合电子流对光的响应机理模型(Ye et al ., 2013a , 2013b )推导出Φ PSII 对光的响应模型, 确定其变化规律与PSII天线色素分子的内禀特性之间的关系; 其次, 利用Φ PSII 对光响应的机理模型、负指数模型和指数模型分别拟合剑叶金鸡菊(Coreopsis lanceolata )、黄荆(Vitex negundo )和大狼杷草(Bidens frondosa )在正常条件下Φ PSII 对光的响应曲线, 判断所推导的Φ PSII 对光的响应模型是否合理和有效, 并与负指数模型和指数模型的拟合结果进行比较, 以确定这些模型的优缺点; 再次, 用所测量的ETR 对光的响应数据验证我们的推测, 即植物的Φ PSII 随光强的增加而下降可能与其天线色素分子的有效光能吸收截面特性密切相关; 最后, 利用所拟合的结果确定LI-6400-40B荧光仪设定的叶片光能吸收系数为0.84和光能在PSII和PSI的分配比例为0.5是否适合剑叶金鸡菊、黄荆和大狼杷草.因此, 这些问题的探讨将为研究植物的Φ PSII 对光的响应以及Φ PSII 随光强的增加而下降的机理提供理论基础, 同时也为研究植物的ETR -I 和Φ PSII -I 提供数学工具. ...
... 式中的符号如φ 、N 0 、S 、g i 、g k 、k P 、k D 、ξ 1 、ξ 2 、ξ 3 、σ ik 和τ 等皆为描述天线色素分子物理特性的参数, 详见相关文献(Ye et al ., 2013a , 2013b ; 叶子飘等, 2014 ), α' 为叶片的光吸收系数, β' 为光能在PSII和PSI两个光系统中的分配比例.其中α' 一般取值为0.84 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ), β' 一般取值为0.5 (Ehleringer & Pearcy, 1983 ; Krall & Edwards, 1992 ; Major & Dunton, 2002 ). ...
... 由公式(1)还我们还可以得到天线色素分子有效光能吸收截面(σ' ik )与光强之间的关系(Ye et al ., 2013a , 2013b )为: ...