

Chin J Plant Ecol ›› 2021, Vol. 45 ›› Issue (9): 1024-1032.DOI: 10.17521/cjpe.2021.0083
Special Issue: 生态学研究的方法和技术
• Methods and techniques • Previous Articles
ZHENG Jing-Ming( ), LIU Hong-Yu
), LIU Hong-Yu
Received:2021-03-10
Accepted:2021-05-19
Online:2021-09-20
Published:2021-11-18
Contact:
ZHENG Jing-Ming
Supported by:ZHENG Jing-Ming, LIU Hong-Yu. Using Strauss-Hardcore model to detect vessel spatial distribution in angiosperms with various vessel configurations[J]. Chin J Plant Ecol, 2021, 45(9): 1024-1032.
Add to citation manager EndNote|Ris|BibTeX
URL: https://www.plant-ecology.com/EN/10.17521/cjpe.2021.0083
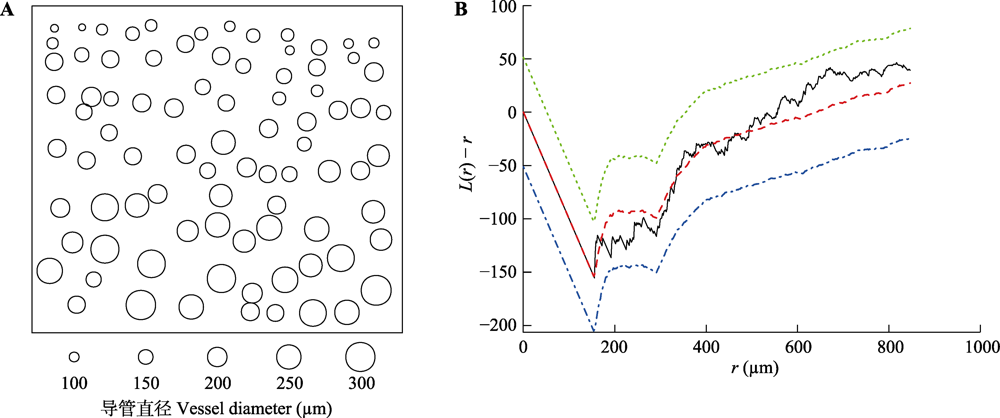
Fig. 1 Spatial distribution of vessels in xylem of Stewartia pseudocamelliashi and envelope test of fitted Strauss-Hardcore (SH) model. A, Distribution of vessels in xylem cross-section. Each cycle stands for a vessel with cycle diameter as vessel diameter (µm). B, Envelope test for L function at significance of 0.05. r, the distance of paired points; Y-axis is the L function defined in equation (3). Black line represents L value from data fitted SH model, red line for average L value from 19 simulation of theoretical SH model, green and blue lines represent 2.5% and 97.5% quantile of L value from 19 simulation of theoretical SH model respectively.
| 模型 Model | 点-过程特点 Point-process characteristic | 适用范围 Scenario for model application |
|---|---|---|
| 空间泊松模型 Poisson model | 空间点位置完全随机 Complete spatial randomness of points | 单一尺度, 单一导管属性, 随机分布特征 Single scale, single vessel identity, random distribution |
| 硬核模型 Hardcore model | 相邻点间距低于硬核距离则不能存在 Neighbor point is forbidden at distance smaller than hardcore distance | 单一尺度, 单一导管属性, 均匀分布特征 Single scale, single vessel identity, uniform distribution |
| 施特劳斯模型 Strauss model | 相邻点间距越小则出现概率越低 Neighbor points have lower probability with smaller distance between them | 单一尺度, 单一导管属性, 聚集分布特征 Single scale, single vessel identity, aggregation distribution |
| 盖耶饱和模型 Geyer saturation model | 任一点全部分布概率不超过特定值 Probability of each point is restrained at specific threshold value | 单一尺度, 单一导管属性, 聚集分布特征, 受导管密度影响 Single scale, single vessel identity, aggregation distribution, influenced by total vessel density |
| 多类型硬核模型 MultiHardcore model | 点属性2类以上的硬核模型 Hardcore model with more than two point identities | 单一尺度, 两类以上导管属性(如早、晚材导管, 单、复导管等), 同类导管均匀分布特征 Single scale, more than two vessel identities (e.g., vessel for early- and latewood, single vessel and multiple vessel), uniform distribution for each identity |
| 多类型施特劳斯模型 MultiStrauss model | 点属性2类以上的施特劳斯模型 Strauss model with more than two point identities | 单一尺度, 两类以上导管属性, 同类导管聚集分布特征 Single scale, more than two vessel identities, aggregation distribution for each identity |
| 斯特劳斯-硬核模型 Strauss-Hardcore model | 一个硬核模型和一个施特劳斯模型的组合 A combination of a Strauss model and a Hardcore model | 两个尺度, 单一属性的导管, 均匀-聚集分布特征 Two scales, single two vessel identity, uniform-aggregation distribution |
| 多类型施特劳斯-硬核模型 MultiStrauss-Hardcore model | 点属性2类以上的斯特劳斯-硬核模型 Strauss-Hardcore model with more than two point identities | 两个尺度, 两类以上导管属性, 同类导管不同尺度上呈均匀和聚集分布特征 Two scales, more than two vessel identities, uniform-aggregation distribution |
| 组合式盖耶模型 Piecewise Geyer model | 组合模型, 可包括多个盖耶饱和子模型、硬核子模型和施特劳斯子模型 A hybrid model including multiple sub-models such as Strauss model, Hardcore model, and Geyer saturation model | 多个尺度, 单一属性的导管, 均匀和聚集分布特征, 受导管总密度影响 More than two scales, single vessel identity, uniform-aggregation distribution, influenced by total vessel density |
Table 2 Characteristics of spatial point-process models for vessel configuration analysis
| 模型 Model | 点-过程特点 Point-process characteristic | 适用范围 Scenario for model application |
|---|---|---|
| 空间泊松模型 Poisson model | 空间点位置完全随机 Complete spatial randomness of points | 单一尺度, 单一导管属性, 随机分布特征 Single scale, single vessel identity, random distribution |
| 硬核模型 Hardcore model | 相邻点间距低于硬核距离则不能存在 Neighbor point is forbidden at distance smaller than hardcore distance | 单一尺度, 单一导管属性, 均匀分布特征 Single scale, single vessel identity, uniform distribution |
| 施特劳斯模型 Strauss model | 相邻点间距越小则出现概率越低 Neighbor points have lower probability with smaller distance between them | 单一尺度, 单一导管属性, 聚集分布特征 Single scale, single vessel identity, aggregation distribution |
| 盖耶饱和模型 Geyer saturation model | 任一点全部分布概率不超过特定值 Probability of each point is restrained at specific threshold value | 单一尺度, 单一导管属性, 聚集分布特征, 受导管密度影响 Single scale, single vessel identity, aggregation distribution, influenced by total vessel density |
| 多类型硬核模型 MultiHardcore model | 点属性2类以上的硬核模型 Hardcore model with more than two point identities | 单一尺度, 两类以上导管属性(如早、晚材导管, 单、复导管等), 同类导管均匀分布特征 Single scale, more than two vessel identities (e.g., vessel for early- and latewood, single vessel and multiple vessel), uniform distribution for each identity |
| 多类型施特劳斯模型 MultiStrauss model | 点属性2类以上的施特劳斯模型 Strauss model with more than two point identities | 单一尺度, 两类以上导管属性, 同类导管聚集分布特征 Single scale, more than two vessel identities, aggregation distribution for each identity |
| 斯特劳斯-硬核模型 Strauss-Hardcore model | 一个硬核模型和一个施特劳斯模型的组合 A combination of a Strauss model and a Hardcore model | 两个尺度, 单一属性的导管, 均匀-聚集分布特征 Two scales, single two vessel identity, uniform-aggregation distribution |
| 多类型施特劳斯-硬核模型 MultiStrauss-Hardcore model | 点属性2类以上的斯特劳斯-硬核模型 Strauss-Hardcore model with more than two point identities | 两个尺度, 两类以上导管属性, 同类导管不同尺度上呈均匀和聚集分布特征 Two scales, more than two vessel identities, uniform-aggregation distribution |
| 组合式盖耶模型 Piecewise Geyer model | 组合模型, 可包括多个盖耶饱和子模型、硬核子模型和施特劳斯子模型 A hybrid model including multiple sub-models such as Strauss model, Hardcore model, and Geyer saturation model | 多个尺度, 单一属性的导管, 均匀和聚集分布特征, 受导管总密度影响 More than two scales, single vessel identity, uniform-aggregation distribution, influenced by total vessel density |
| [1] | Adams HD, Zeppel MJB, Anderegg WRL, Hartmann H, Landhäusser SM, Tissue DT, Huxman TE, Hudson PJ, Franz TE, Allen CD, Anderegg LDL, Barron-Gafford GA, Beerling DJ, Breshears DD, Brodribb TJ, et al. (2017). A multi-species synthesis of physiological mechanisms in drought-induced tree mortality. Nature Ecology & Evolution, 1, 1285-1291. |
| [2] | Baddeley A, Turner R (2005). Spatstat: an R package for analyzing spatial point patterns. Journal of Statistical Software, 12, 1-42. |
| [3] | Baddeley A, Rubak E, Turner R (2015). Spatial Point Patterns: Methodology and Applications with R. CRC Press, New York. |
| [4] |
Beeckman H (2016). Wood anatomy and trait-based ecology. IAWA Journal, 37, 127-151.
DOI URL |
| [5] | Carlquist S (2001). Comparative Wood Anatomy. Springer, Berlin. |
| [6] | Carlquist S (2009). Non-random vessel distribution in woods: patterns, modes, diversity, correlations. Aliso, 27, 39-58. |
| [7] |
Carlquist S (2012). How wood evolves: a new synthesis. Botany, 90, 901-940.
DOI URL |
| [8] |
Choat B, Brodribb TJ, Brodersen CR, Duursma RA, López R, Medlyn BE (2018). Triggers of tree mortality under drought. Nature, 558, 531-539.
DOI URL |
| [9] |
Choat B, Jansen S, Brodribb TJ, Cochard H, Delzon S, Bhaskar R, Bucci SJ, Feild TS, Gleason SM, Hacke UG, Jacobsen AL, Lens F, Maherali H, Martínez-Vilalta J, Mayr S, et al. (2012). Global convergence in the vulnerability of forests to drought. Nature, 491, 752-755.
DOI URL |
| [10] |
García-Cervigón AI, Olano JM, von Arx G, Fajardo A (2018). Xylem adjusts to maintain efficiency across a steep precipitation gradient in two coexisting generalist species. Annals of Botany, 122, 461-472.
DOI PMID |
| [11] | Hacke UG, Spicer R, Schreiber SG, Plavcová L (2017). An ecophysiological and developmental perspective on variation in vessel diameter. Plant, Cell & Environment, 40, 831-845. |
| [12] |
IAWA Committee (1989). IAWA list of microscopic features for hardwood identification. IAWA Bulletin, 10, 219-332.
DOI URL |
| [13] |
Jacobsen AL, Pratt RB, Tobin MF, Hacke UG, Ewers FW (2012). A global analysis of xylem vessel length in woody plants. American Journal of Botany, 99, 1583-1591.
DOI PMID |
| [14] |
Jacobsen AL, Valdovinos-Ayala J, Pratt RB (2018). Functional lifespans of xylem vessels: development, hydraulic function, and post-function of vessels in several species of woody plants. American Journal of Botany, 105, 142-150.
DOI PMID |
| [15] | Johnson D, Eckart P, Alsamadisi N, Noble H, Martin C, Spicer R (2018). Polar auxin transport is implicated in vessel differentiation and spatial patterning during secondary growth in Populus. American Journal of Botany, 105, 186-196. |
| [16] |
Loepfe L, Martinez-Vilalta J, Piñol J, Mencuccini M (2007). The relevance of xylem network structure for plant hydraulic efficiency and safety. Journal of Theoretical Biology, 247, 788-803.
PMID |
| [17] |
Martínez-Vilalta J, Mencuccini M, Álvarez X, Camacho J, Loepfe L, Piñol J (2012). Spatial distribution and packing of xylem conduits. American Journal of Botany, 99, 1189- 1196.
DOI PMID |
| [18] |
Mencuccini M, Martinez-Vilalta J, Piñol J, Loepfe L, Burnat M, Alvarez X, Camacho J, Gil D (2010). A quantitative and statistically robust method for the determination of xylem conduit spatial distribution. American Journal of Botany, 97, 1247-1259.
DOI PMID |
| [19] | Mrad A, Domec JC, Huang CW, Lens F, Katul G (2018). A network model links wood anatomy to xylem tissue hydraulic behaviour and vulnerability to cavitation. Plant, Cell & Environment, 41, 2718-2730. |
| [20] | Panshin AJ, Zeeuw CD (1980). Textbook of Wood Technology: Structure, Identification, Uses Properties of Commercial Woods in the United States and Canada. McGraw-Hill Publishing Company, New York. |
| [21] |
Perry GLW, Miller BP, Enright NJ (2006). A comparison of methods for the statistical analysis of spatial point patterns in plant ecology. Plant Ecology, 187, 59-82.
DOI URL |
| [22] |
Pfautsch S (2016). Hydraulic anatomy and function of trees- Basics and critical developments. Current Forestry Reports, 2, 236-248.
DOI URL |
| [23] | R Core Team (2015). R: a Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. |
| [24] |
Rueden CT, Schindelin J, Hiner MC, DeZonia BE, Walter AE, Arena ET, Eliceiri KW (2017). ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinformatics, 18, 529.
DOI URL |
| [25] |
Schenk HJ (2018). Wood: biology of a living tissue. American Journal of Botany, 105, 139-141.
DOI URL |
| [26] |
Scholz A, Klepsch M, Karimi Z, Jansen S (2013). How to quantify conduits in wood? Frontiers in Plant Science, 4, 56. DOI: 10.3389/fpls.2013.00056.
DOI |
| [27] | Schweingruber FH, Börner A, Schulze ED (2008). Atlas of Woody Plant Stems: Evolution, Structure, and Environmental Modifications. Springer, Berlin. |
| [28] |
Sievänen R, Godin C, DeJong TM, Nikinmaa E (2014). Functional-structural plant models: a growing paradigm for plant studies. Annals of Botany, 114, 599-603.
PMID |
| [29] |
von Arx G, Kueffer C, Fonti P (2013). Quantifying plasticity in vessel grouping-added value from the image analysis tool ROXAS. IAWA Journal, 34, 433-445.
DOI URL |
| [30] |
Wheeler EA, Baas P (1998). Wood identification-A review. IAWA Journal, 19, 241-264.
DOI URL |
| [1] | ZHANG Qiao-Ying, ZHANG Yun-Chun, LUO Peng, WANG Qian, WU Ning. ECOLOGICAL CHARACTERISTICS OF A SABINA SALTUARIA POPULATION AT TIMBERLINE ON THE SOUTH-FACING SLOPE OF BAIMA SNOW MOUNTAIN, SOUTHWEST CHINA [J]. Chin J Plant Ecol, 2007, 31(5): 857-864. |
| [2] | FAN Da-Yong, XIE Zong-Qiang. Several Controversial Viewpoints in Studying the Cavitation of Xylem Vessels [J]. Chin J Plant Ecol, 2004, 28(1): 126-132. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © 2022 Chinese Journal of Plant Ecology
Tel: 010-62836134, 62836138, E-mail: apes@ibcas.ac.cn, cjpe@ibcas.ac.cn