

Chin J Plant Ecol ›› 2017, Vol. 41 ›› Issue (3): 378-385.DOI: 10.17521/cjpe.2016.0067
• Method and Technology • Previous Articles
Ji-Ye ZENG1, Zheng-Hong TAN2,*( ), Nobuko SAIGUSA1
), Nobuko SAIGUSA1
Online:2017-03-10
Published:2017-04-12
Contact:
Zheng-Hong TAN
About author:KANG Jing-yao(1991-), E-mail: Ji-Ye ZENG, Zheng-Hong TAN, Nobuko SAIGUSA. Using approximate Bayesian computation to infer photosynthesis model parameters[J]. Chin J Plant Ecol, 2017, 41(3): 378-385.
Add to citation manager EndNote|Ris|BibTeX
URL: https://www.plant-ecology.com/EN/10.17521/cjpe.2016.0067
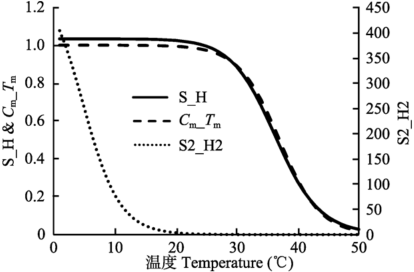
Fig. 1 Comparison of the temperature correction models. Solid line is the curve of von Caemmerer et al. (2009) when S = 710 and H = 220 000; dotted line is the curve when S is increased by 10% (S=790, H=220 000); dashed line is the curve calculated according to our new response curve (Cm = 0.3, Tm = 37).
| 符号 Symbol | 单位 Units | 注释 Remark | 参考值 Reference value |
|---|---|---|---|
| A | μmol·m-2·s-1 | 净光合速率 Net photosynthesis rate | |
| Ac | μmol·m-2·s-1 | Rubisco酶限制下的光合速率 Rubisco activity limited net photosynthesis rate | |
| Aj | μmol·m-2·s-1 | RuBP再生限制的光合速率 Electron transport limited net photosynthesis rate | |
| Rd | μmol·m-2·s-1 | 呼吸速率 Respiration rate | |
| Ci | μbar | 胞内CO2分压 Intercellular CO2 partial pressure | |
| Ca | μbar | 大气CO2分压 Air CO2 partial pressure | |
| Cs | μbar | 叶面CO2分压 Leaf-surface CO2 partial pressure | |
| Γ* | μbar | CO2补偿点 CO2 compensation point | |
| Vcmax | μmol·m-2·s-1 | 最大羧化速率 Maximal rubisco carboxylase rate | |
| Jmax | μmol·m-2·s-1 | 最大电子传输速率 Maximal electronic transport rate | |
| J | μmol·m-2·s-1 | 电子传输速率 Electronic transport rate | |
| I2 | μmol·m-2·s-1 | 电子传输速率 Electronic transport rate through photosystem II | |
| I0 | μmol·m-2·s-1 | 光照强度 Photon flux density | |
| f | 光谱校正常数 Fraction of effective photon flux | 0.15 | |
| α | 转化率 Conversion efficiency | 0.15 | |
| Oi | mbar | 胞内氧分压 Intercellular O2 partial pressure | 210 |
| Ko | mbar | 氧化酶的动力学常数 Michaelis-Menten constant of Rubisco for O2 | |
| Kc | μbar | 羧化酶的动力学常数 Michaelis-Menten constant of Rubisco for CO2 | |
| gb | mol·m-2·s-1 | 边界层导度 Boundary-layer conductance | |
| gs | mol·m-2·s-1 | 气孔导度 Stomatal conductance | |
| g0 | mol·m-2·s-1 | 气孔最小导度 Minimum stomatal conductance | 0.01 |
| g1 | 气孔导度常数 Sensitivity coefficient of stomatal conductance | 10.0 | |
| hs | 叶面相对湿度 Relative humidity on leaf surface | ||
| WS | m·s-1 | 风速 Wind speed | |
| LeafW | m | 叶片宽度 Leaf width | |
| V25, J25, Kc25, Ko25, Rd25, Γ*25 | 相应参数在25 ℃的值 Values at 25 °C | 分别为80, 160, 260, 165, 1, 38 respectively | |
| Ea | J·mol-1 | 活化能 Activation energy | 分别为58 500, 37 000, 59 400, 36 000, 66 400, 23 400 respectively |
| TK | K | 温度 Temperature | |
| TC | °C | 温度 Temperature | |
| R | J·K-1·mol-1 | 气体常数 Gas constant | 8.314 |
| S | J·K-1·mol-1 | 电子传输速率的温度参数 Entropy term | 650 |
| H | J·mol-1 | 曲率参数 Deactivation energy | 200 000 |
| Cm | °C-1 | 温度修正参数 Temperature modification constant | |
| Tm | °C | 温度修正参数 Temperature modification constant | |
| VTm | μmol·m-2·s-1 | 羧化速率参数 Rubisco carboxylase rate | |
| JTm | μmol·m-2·s-1 | 电子传输速率参数 Potential rate of electron transport | |
| NEE | μmol·m-2·s-1 | 有效净生态系统CO2交换率 Net ecosystem exchange | |
| PPFD | μmol·m-2·s-1 | 有效光量子流密度 Photosynthetic photon flux density | |
| P2 | kPa | 大气压 Air pressure | |
| LAI | 叶面积指数 Leaf area index |
Table 2 Variables and parameters used in the photosynthesis model and their reference values mainly from Caemmerer et al. (2009)
| 符号 Symbol | 单位 Units | 注释 Remark | 参考值 Reference value |
|---|---|---|---|
| A | μmol·m-2·s-1 | 净光合速率 Net photosynthesis rate | |
| Ac | μmol·m-2·s-1 | Rubisco酶限制下的光合速率 Rubisco activity limited net photosynthesis rate | |
| Aj | μmol·m-2·s-1 | RuBP再生限制的光合速率 Electron transport limited net photosynthesis rate | |
| Rd | μmol·m-2·s-1 | 呼吸速率 Respiration rate | |
| Ci | μbar | 胞内CO2分压 Intercellular CO2 partial pressure | |
| Ca | μbar | 大气CO2分压 Air CO2 partial pressure | |
| Cs | μbar | 叶面CO2分压 Leaf-surface CO2 partial pressure | |
| Γ* | μbar | CO2补偿点 CO2 compensation point | |
| Vcmax | μmol·m-2·s-1 | 最大羧化速率 Maximal rubisco carboxylase rate | |
| Jmax | μmol·m-2·s-1 | 最大电子传输速率 Maximal electronic transport rate | |
| J | μmol·m-2·s-1 | 电子传输速率 Electronic transport rate | |
| I2 | μmol·m-2·s-1 | 电子传输速率 Electronic transport rate through photosystem II | |
| I0 | μmol·m-2·s-1 | 光照强度 Photon flux density | |
| f | 光谱校正常数 Fraction of effective photon flux | 0.15 | |
| α | 转化率 Conversion efficiency | 0.15 | |
| Oi | mbar | 胞内氧分压 Intercellular O2 partial pressure | 210 |
| Ko | mbar | 氧化酶的动力学常数 Michaelis-Menten constant of Rubisco for O2 | |
| Kc | μbar | 羧化酶的动力学常数 Michaelis-Menten constant of Rubisco for CO2 | |
| gb | mol·m-2·s-1 | 边界层导度 Boundary-layer conductance | |
| gs | mol·m-2·s-1 | 气孔导度 Stomatal conductance | |
| g0 | mol·m-2·s-1 | 气孔最小导度 Minimum stomatal conductance | 0.01 |
| g1 | 气孔导度常数 Sensitivity coefficient of stomatal conductance | 10.0 | |
| hs | 叶面相对湿度 Relative humidity on leaf surface | ||
| WS | m·s-1 | 风速 Wind speed | |
| LeafW | m | 叶片宽度 Leaf width | |
| V25, J25, Kc25, Ko25, Rd25, Γ*25 | 相应参数在25 ℃的值 Values at 25 °C | 分别为80, 160, 260, 165, 1, 38 respectively | |
| Ea | J·mol-1 | 活化能 Activation energy | 分别为58 500, 37 000, 59 400, 36 000, 66 400, 23 400 respectively |
| TK | K | 温度 Temperature | |
| TC | °C | 温度 Temperature | |
| R | J·K-1·mol-1 | 气体常数 Gas constant | 8.314 |
| S | J·K-1·mol-1 | 电子传输速率的温度参数 Entropy term | 650 |
| H | J·mol-1 | 曲率参数 Deactivation energy | 200 000 |
| Cm | °C-1 | 温度修正参数 Temperature modification constant | |
| Tm | °C | 温度修正参数 Temperature modification constant | |
| VTm | μmol·m-2·s-1 | 羧化速率参数 Rubisco carboxylase rate | |
| JTm | μmol·m-2·s-1 | 电子传输速率参数 Potential rate of electron transport | |
| NEE | μmol·m-2·s-1 | 有效净生态系统CO2交换率 Net ecosystem exchange | |
| PPFD | μmol·m-2·s-1 | 有效光量子流密度 Photosynthetic photon flux density | |
| P2 | kPa | 大气压 Air pressure | |
| LAI | 叶面积指数 Leaf area index |
| 参数 Parameter | 参数值下限 Lower value | 参数值上限 Upper value | 实际模拟值 Inversed value | |
|---|---|---|---|---|
| Vcmax | Vopt | 10 | 500 | 374 |
| Ea | 10 000 | 70 000 | 21 287 | |
| Jmax | Jopt | 10 | 500 | 310 |
| Ea | 10 000 | 50 000 | 10 000 | |
| Rd | Rd25 | 0 | 10 | 10 |
| Ea | 10 000 | 70 000 | 10 033 | |
| Cm | 0.25 | 0.50 | 0.28 | |
| Tm | 20.0 | 50.0 | 26.9 | |
| g1 | 0.0 | 10.0 | 3.7 |
Table 3 Initial parameter ranges and modeled values
| 参数 Parameter | 参数值下限 Lower value | 参数值上限 Upper value | 实际模拟值 Inversed value | |
|---|---|---|---|---|
| Vcmax | Vopt | 10 | 500 | 374 |
| Ea | 10 000 | 70 000 | 21 287 | |
| Jmax | Jopt | 10 | 500 | 310 |
| Ea | 10 000 | 50 000 | 10 000 | |
| Rd | Rd25 | 0 | 10 | 10 |
| Ea | 10 000 | 70 000 | 10 033 | |
| Cm | 0.25 | 0.50 | 0.28 | |
| Tm | 20.0 | 50.0 | 26.9 | |
| g1 | 0.0 | 10.0 | 3.7 |
| 对每一个APMC粒子 For all particles for k = 1 to Nobs do(对所有的观测数据) For all observations 用APMC粒子选定的V25, J25, Rd25, g1, Ea, Cm, Tm Use parameter values selected by AMPC 计算Vcmax, Jmax, Rd, gb Estimate target model parameters 设t = 1 (Ci的迭代计算次数) At initial time 设\(C_i^0=0.7C_a\) Set the intercellular CO2 equal to 70% of air CO2 设\(\Delta C_i >1\) Set the intercellular CO2 not in equilibrant While \(\Delta C_i >1 \) do 计算 Ac, Aj Compute the two rate. 计算\(A=\frac{A_c+A_j-\sqrt{(A_c+A_j)^2-4\times 0.98A_cA_j}}{2\times 0.98} \\ Compute the joint rate 计算\\ C_i^t=C_a-\frac{A}{g_b}-\frac{g_bC_aA-A^2}{g_bg_1h_sA-g_0A+g_0Ag_bg_oC_a}\) Compute the intercellular CO2 \( \Delta C_i=|C_i^t-C_i^{t-1}|\) Check equilibrant state 设t = t + 1 Advance time end while end for 将|A-NEE|的平均值作为APMC粒子的r Calculate the difference between modeled photosynthesis rate and the observed rate |
Appendix I Model entity in the APMC
| 对每一个APMC粒子 For all particles for k = 1 to Nobs do(对所有的观测数据) For all observations 用APMC粒子选定的V25, J25, Rd25, g1, Ea, Cm, Tm Use parameter values selected by AMPC 计算Vcmax, Jmax, Rd, gb Estimate target model parameters 设t = 1 (Ci的迭代计算次数) At initial time 设\(C_i^0=0.7C_a\) Set the intercellular CO2 equal to 70% of air CO2 设\(\Delta C_i >1\) Set the intercellular CO2 not in equilibrant While \(\Delta C_i >1 \) do 计算 Ac, Aj Compute the two rate. 计算\(A=\frac{A_c+A_j-\sqrt{(A_c+A_j)^2-4\times 0.98A_cA_j}}{2\times 0.98} \\ Compute the joint rate 计算\\ C_i^t=C_a-\frac{A}{g_b}-\frac{g_bC_aA-A^2}{g_bg_1h_sA-g_0A+g_0Ag_bg_oC_a}\) Compute the intercellular CO2 \( \Delta C_i=|C_i^t-C_i^{t-1}|\) Check equilibrant state 设t = t + 1 Advance time end while end for 将|A-NEE|的平均值作为APMC粒子的r Calculate the difference between modeled photosynthesis rate and the observed rate |
| [1] | Amthor JS (1994). Scaling CO2-photosynthesis relationships from the leaf to the canopy. Photosynthesis Research, 39, 321-350. |
| [2] | Andrieu C, Doucet A, Holenstein R (2010). Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society, Series B, 72, 269-342. |
| [3] | Baldocchi D (1994). An analytical solution for coupled leaf photosynthesis and stomata1 conductance models. Tree Physiology, 14, 1069-1079. |
| [4] | Ball JT, Woodrow JT, Berry JA (1987). A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In: Biggins J ed. Progress in Photosynthesis Research, Vol. 4. Proceedings of the 7th International Congress on Photosynthesis. Matins Nijhoff, Dordrecht, the Netherlands. 221-224. |
| [5] | Beaumont MA (2010). Approximate Bayesian computation in evolution and ecology. Annual Review of Ecology, Evolution, and Systematics, 41, 379-406. |
| [6] | Csilléry K, Blum MGB, Gaggiotti OE, Francois O (2010). Approximate Bayesian Computation (ABC) in practice. Trends in Ecology and Evolution, 25, 410-418. |
| [7] | Cubasch U, Wuebbles D, Chen D, Facchini MC, Frame D, Mahowald N, Winther JG (2013). Introduction. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM eds. Climate Change 2013: The Physical Science Basis. Cambridge University Press, Cambridge, UK. |
| [8] | Dai Y, Dickinson RE, Wang YP (2004). A Two-Big-Leaf Model for canopy temperature, photosynthesis, and stomatal conductance. Journal of Climate, 17, 2281-2299. |
| [9] | Damour G, Simonneau T, Cochard H, Urban L (2010). An overview of models of stomatal conductance at the leaf level. Plant, Cell & Environment, 33, 1419-1438. |
| [10] | de Pury DGG, Farquhar GD (1997). Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant, Cell & Environment, 20, 537-557. |
| [11] | Farquhar GD, von Caemmerer S, Berry JA (1980). A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta, 149, 78-90. |
| [12] | Gao M, Zhang H (2012). Sequential Monte Carlo methods for parameter estimation in nonlinear state-space models. Computers and Geosciences, 44, 70-77. |
| [13] | Groenendijk M, Dolman AJ, Ammann C, Arneth A, Cescatti A, Dragoni D, Gash JHC, Gianelle D, Gioli B, Kiely G, Knohl A, Law BE, Lund M, Marcolla B, van der Molen MK, Montagnani L, Moors E, Richardson AD, Roupsard O, Verbeeck H, Wohlfahrt G (2011). Seasonal variation of photosynthetic model parameters and leaf area index from global Fluxnet eddy covariance data. Journal of Geoph¬ysical Research, 116, G04027. doi:10.1029/2011JG001742. |
| [14] | Gu L (2010). Reliable estimation of biochemical parameters from C3 leaf photosynthesis-intercellular carbon dioxide response curves. Plant, Cell & Environment, 33, 1852-1874. |
| [15] | Hartig F, Dislich C, Wiegand T, Huth A (2014). Technical note: Approximate Bayesian parameterization of a process-based tropical forest model. Biogeosciences, 11, 1261-1272. |
| [16] | Hirano T, Hirata R, Fujinuma Y, Saigusa N, Yamamoto S, Harazono Y, Takada M, Inukai K, Inoue G (2003). CO2 and water vapor exchange of a larch forest in northern Japan. Tellus, 55B, 244-257. |
| [17] | Jarvis PG (1995). Scaling processes and problems. Plant, Cell & Environment, 18, 1079-1089. |
| [18] | June T, Evans JR, Farquhar GD (2004). A simple new equation for the reversible temperature dependence of photosynthetic electron transport: A study on soybean leaf. Functional Plant Biology, 31, 275-283. |
| [19] | Kosugi Y, Takanashi S, Ueyama M, Ohkubo S, Tanaka H, Matsumoto K, Yoshifuji N, Ataka M, Sakabe A (2013). Determination of the gas exchange phenology in an evergreen coniferous forest from 7 years of eddy covariance flux data using an extended big-leaf analysis. Ecological Research, 28, 373-385. |
| [20] | Lenormand M, Jabot F, Deffuant G (2013). Adaptive approximate Bayesian computation for complex models. Computational Statistics, 28, 2777-2796. |
| [21] | MacEachern SN, Clyde M, Liu J (1999). Sequential importance sampling for nonparametric Bayes models: The next generation. Canadian Journal of Statistics, 27, 251-267. |
| [22] | Marin JM, Pudlo P, Robert CP, Ryder RJ (2012). Approximate Bayesian computational methods. Statistics and Computing, 22, 1167-1180. |
| [23] | Medlyn BE, Dreyer E, Ellsworth D, Forstreuter M, Harley PC, Kirschbaum MUF, Le Roux X, Montpied P, Strassemeyer J, Walcroft A, Wang K, Loustau D (2002a). Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant, Cell & Environment, 25, 1167-1179. |
| [24] | Medlyn BE, Loustau D, Delzon S (2002b). Temperature response of parameters of a biochemically based model of photosynthesis. I. Seasonal changes in mature maritime pine (Pinus pinaster Ait.). Plant, Cell & Environment, 25, 1155-1165. |
| [25] | Saigusa N, Yamamoto S, Hirata R, Ohtani Y, Ide R, Asanuma J, Gamo M, Hirano T, Kondo H, Kosugi Y, Li S-G, Nakai Y, Takagi K, Tani M, Wang H (2008). Temporal and spatial variations in the seasonal patterns of CO2 flux in boreal, temperate, and tropical forests in East Asia. Agricultural and Forest Meteorology, 148, 700-713. |
| [26] | Sellers PJ, Randall DA, Collatz GJ, Berry JA, Field CB, Dazlich DA, Zhang C, Collelo GD, Bounoua L (1996). A revised land surface parameterization (SiB2) for atmospheric GCMs. Part 1: Model formulation. Journal of Climate, 9, 676-705. |
| [27] | Sprintsin M, Chen JM, Desai A, Gough CM (2012). Evaluation of leaf-to-canopy upscaling methodologies against carbon flux data in North America. Journal of Geophysical Research, 117, G01023. doi:10.1029/2010JG001407. |
| [28] | Toni T, Welch D, Strelkowa N, Ipsen A, Stumpf MPH (2009). Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. Journal of the Royal Society Interface, 6, 187-202. |
| [29] | von Caemmerer S, Farquhar G, Berry J (2009). Biochemical model of C3 photosynthesis. In: Laisk A, Nedbal L, Govindjee eds. Photosynthesis in Silico: Understanding Complexity from Molecules to Ecosystems. Springer, Dordrecht, the Netherlands. 209-230. |
| [30] | Vrugt JA, Sadegh M (2013). Toward diagnostic model calibration and evaluation: Approximate Bayesian computation. Water Resources Research, 49, 4335-4345. |
| [31] | Wang H, Saigusa N, Yamamoto S, Kondo H, Hirano T, Toriyama A, Fujinuma F (2004). Net ecosystem CO2 exchange over a larch forest in Hokkaido, Japan. Atmospheric Environment, 38, 7021-7032. |
| [32] | Wang YP, Leuning R (1998). A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I: Model description and comparison with a multi- layered model. Agricultural and Forest Meteorology, 91, 89-111. |
| [33] | Xu L, Baldocchi DD (2003). Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree Physiology, 23, 865-877. |
| [34] | Yin X, Struik PC (2009). C3 and C4 photosynthesis models: An overview from the perspective of crop modelling. Wageningen Journal of Life Sciences, 57, 27-38. |
| [1] | HAO Yan-Bin, WANG Yan-Fen, CUI Xiao-Yong. Drought stress reduces the carbon accumulation of the Leymus chinensis steppe in Inner Mongolia, China [J]. Chin J Plant Ecol, 2010, 34(8): 898-906. |
| [2] | ZHANG Li, YU Gui-Rui, LUO Yiqi, HE Hong-Lin, ZHANG Lei-Ming. CARBON CYCLE MODELING OF A BROAD-LEAVED KOREAN PINE FOREST IN CHANGBAI MOUNTAIN OF CHINA USING THE MODEL-DATA FUSION APPROACH [J]. Chin J Plant Ecol, 2009, 33(6): 1044-1055. |
| [3] | ZHANG Mi, YU Gui-Rui, ZHANG Lei-Ming, SUN Xiao-Min, WEN Xue-Fa, HAN Shi-Jie. EFFECTS OF SOLAR RADIATION ON NET ECOSYSTEM EXCHANGE OF BROADLEAVED-KOREAN PINE MIXED FOREST IN CHANGBAI MOUNTAIN, CHINA [J]. Chin J Plant Ecol, 2009, 33(2): 270-282. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © 2022 Chinese Journal of Plant Ecology
Tel: 010-62836134, 62836138, E-mail: apes@ibcas.ac.cn, cjpe@ibcas.ac.cn