Selection of null models in nestedness pattern detection of highly asymmetric mycorrhizal networks

doi:10.17521/cjpe.2019.0065

Abstract

Abstract:

Aims Null model is an important basis for nesting judgment. Highly asymmetric structures often appear in plant symbolic fungal networks. This study aims to explore the influence of matrix asymmetric changes on network nesting judgment.
Methods The study was conducted based on various null model construction methods.
Important findings Constraints vary with changing null models, with reducing null space when additional qualifications were added during null model establishment. Highly constrained nulls are prone to causing type II errors. Highly asymmetric networks increase matrix temperature (NT) deviation based on random (Equiprobable- equiprobable, r00) null model while reducing overlap and decreasing fill (NODF) deviation. Values of z-score show that highly asymmetric networks contribute to the significant determination level of NT and NODF. The impacts on the judgment of nestedness of asymmetric networks differ between row and column fixed null models. The effects of network asymmetry change on nesting detection based on column constrained (c0) nulls are similar to that of random null model, but with smaller nesting deviation and standard deviations. No significant differences in both NT and NT deviations were observed among different asymmetry networks based on the row fixed (r0) nulls, with a lower NODF deviation in highly asymmetric network based on c0 nulls. To more accurately determine whether the asymmetric networks would have nested structures, we recommend using a combination of random and constrained null models. Our results also demonstrate that the r0 null model performs better than either the r00 null model or the c0 null model when comparing nesting level of different asymmetric networks.

Key words: interaction network, nestedness, null model, web asymmetry

LIN Li-Tao, MA Ke-Ming. Selection of null models in nestedness pattern detection of highly asymmetric mycorrhizal networks[J]. Chin J Plant Ecol, 2019, 43(7): 611-623.

Add to citation manager EndNote|Ris|BibTeX

URL: https://www.plant-ecology.com/EN/10.17521/cjpe.2019.0065

https://www.plant-ecology.com/EN/Y2019/V43/I7/611

Figures/Tables 10

Table 1 Characteristics of various nestedness metrics

指标 Index	反映特征 Underlying feature	下限保守 Bottom boundary conservative	上限保守 Top boundary conservative	零模型保守 Null model conservative	存在上限 Top limit
矩阵温度 matrix temperature (NT)	矩阵中异常点数量、位置 Relative abundance and position of unexpected absences or presences in a matrix	是 Yes	是 Yes	否 No	是 Yes
配对重叠度 nestedness metric based on overlap and decreasing fill (NODF)	矩阵配对重叠中非子集行列的数量及位置 Percentage and position of columns (rows) overlaps with other columns (rows)	是 Yes	是 Yes	是 Yes	是 Yes
嵌套性偏移 Nestedness deviation	网络与零模型的距离 Distance deviates from null models	是 Yes	否 No	是 Yes	是 Yes
标准化指数 Standardized effect size	网络达到显著水平的难易程度 Significance of a network deviates from null models	是 Yes	否 No	是 Yes	否 No

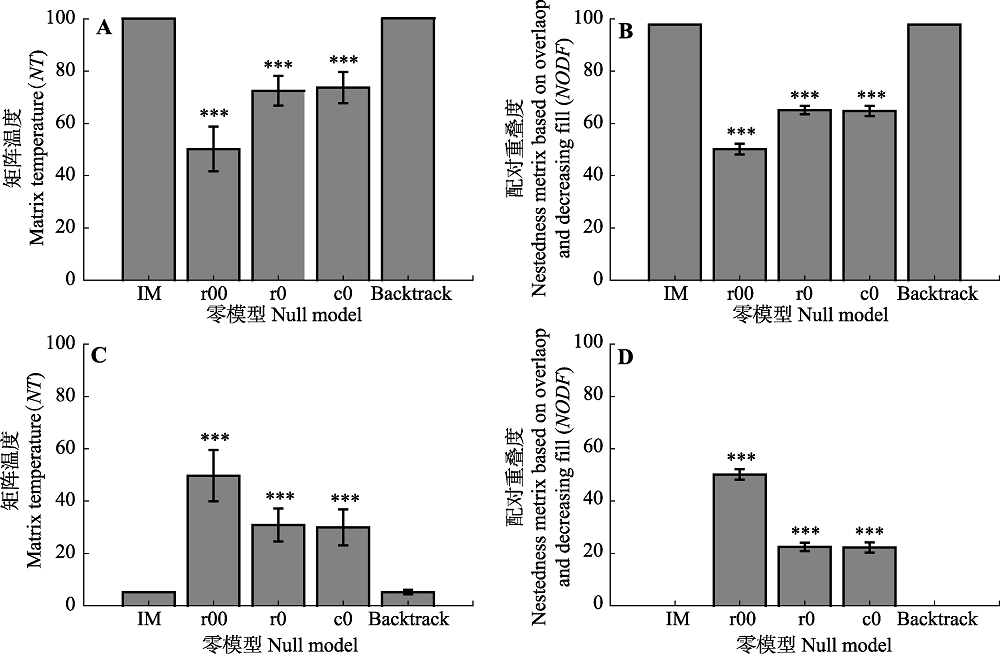
Fig. 1 Absolute values of nestedness from null models constructed based on fully nested (A, B) and uniformly distributed matrices (C, D) (mean ± SD). Backtrack, fixed row-fixed column; c0, equiprobable row-fixed column; IM, initial matrix; r0, fixed row- equiprobable column; r00, equiprobable row-equiprobable column. ***, significant at 0.001 level.

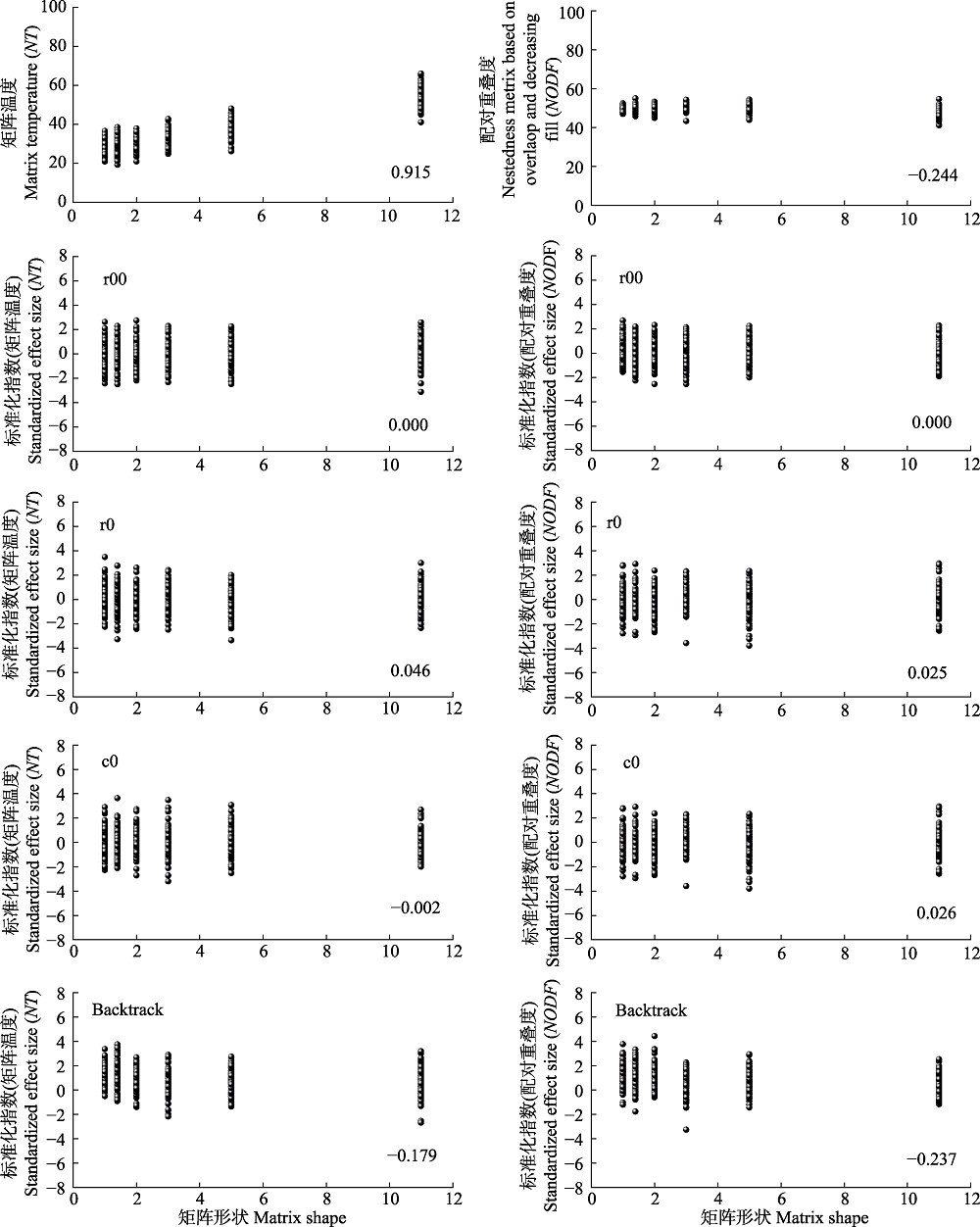
Fig. 2 Effects of changes in matrix shape on nestedness metrics. Matrix shape, number of columns/number of rows. Backtrack, fixed row-fixed column; c0, equiprobable row-fixed column; r0, fixed row-equiprobable column; r00, equiprobable row-equiprobable column.

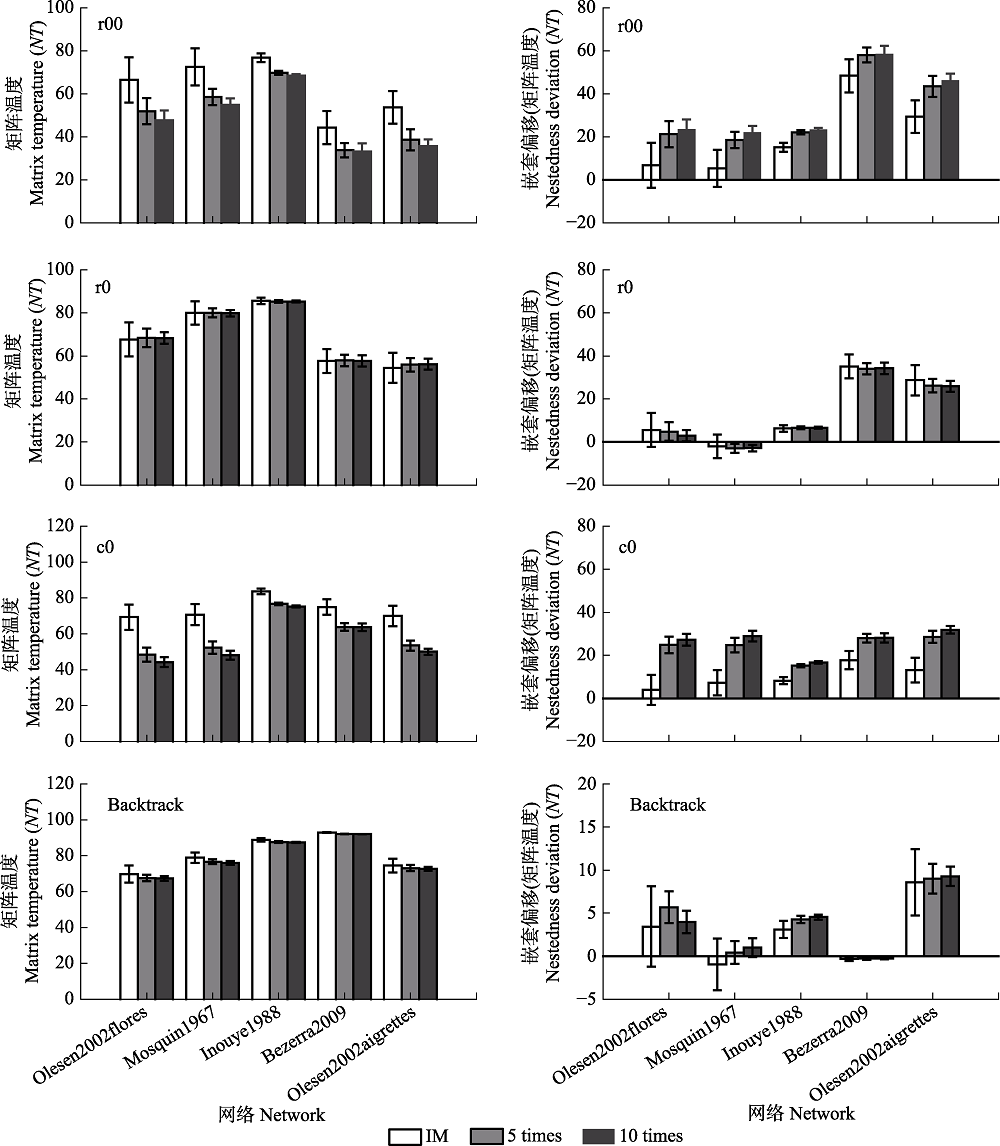
Fig. 3 Effects of matrix asymmetric variations on matrix temperature (NT) and NT deviation based on different binary matrix construction methods (mean ± SD). Backtrack, fixed row-fixed column; c0, equiprobable row-fixed column; r0, fixed row-equiprobable column; r00, equiprobable row-equiprobable column. IM, Initial matrix; 5 times, 5 times column merge network; 10 times, 10 times column merge network.

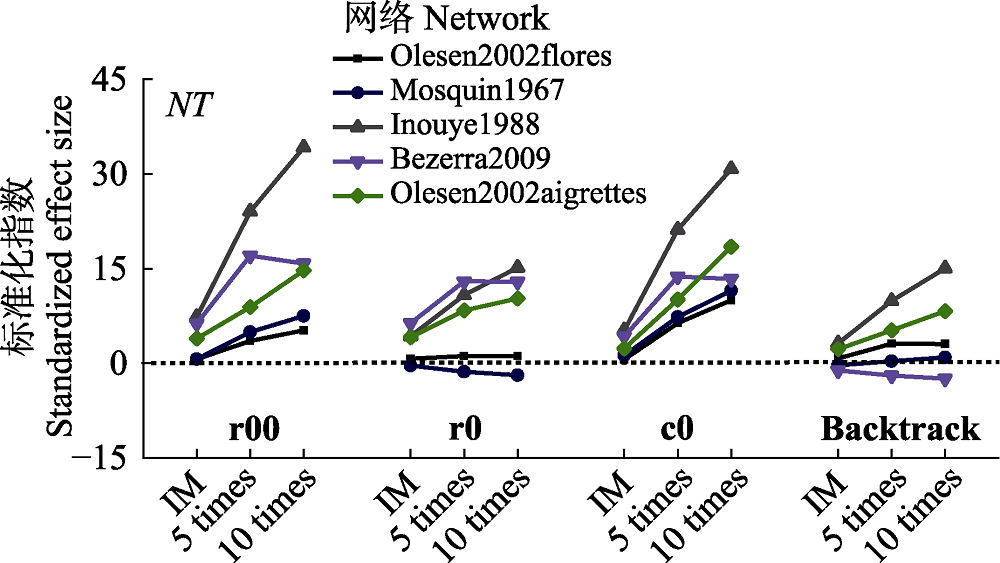
Fig. 4 Effects of matrix asymmetric variations on the standardized effect size (z-score) of matrix temperature (NT). Backtrack, fixed row-fixed column; c0, equiprobable row-fixed column; r0, fixed row-equiprobable column; r00, equiprobable row-equiprobable column. IM, initial matrix; 5 times, 5 times column merge network; 10 times, 10 times column merge network.

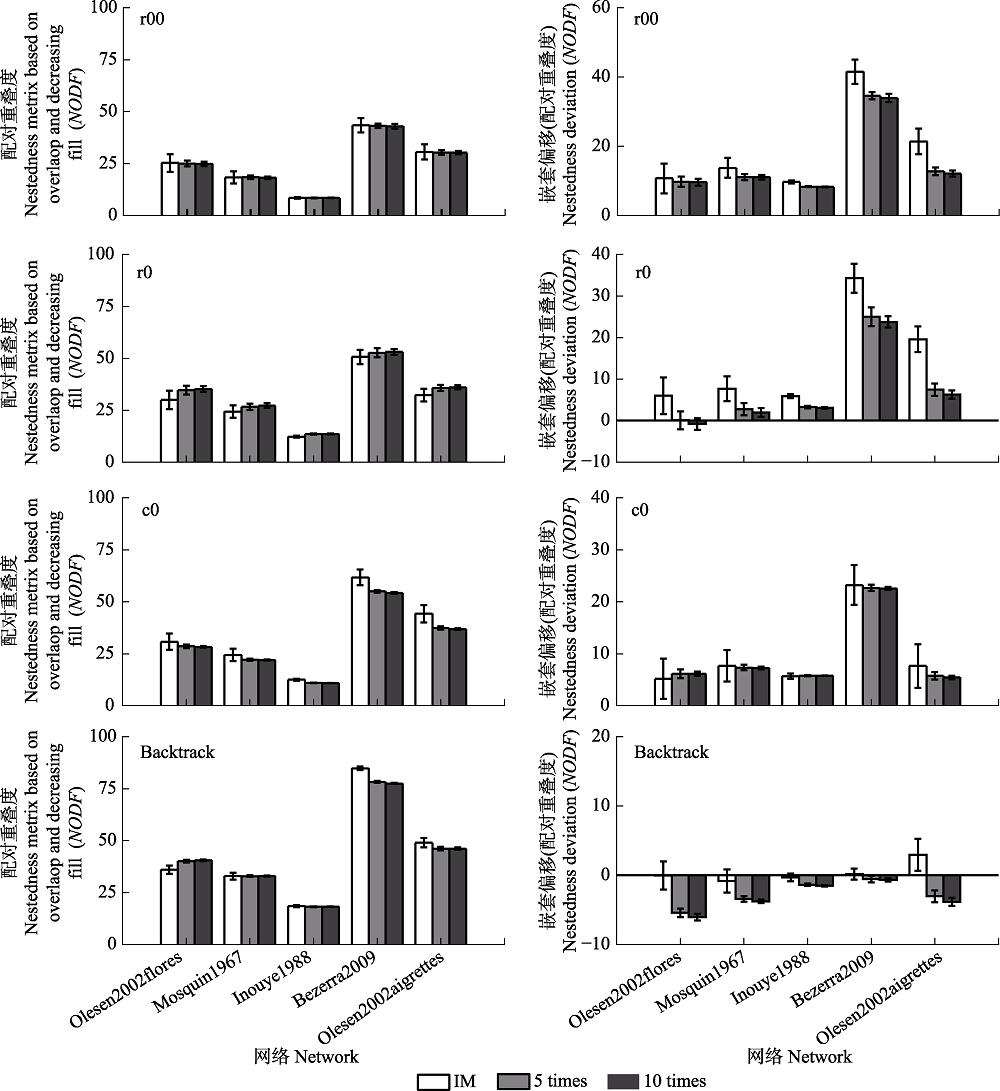
Fig. 5 Effects of matrix asymmetric variations on nestedness metric based on overlap and decreasing fill (NODF) and NODF deviation based on different binary matrix construction methods (mean ± SD). Backtrack, fixed row-fixed column; c0, equiprobable row-fixed column; r0, fixed row-equiprobable column; r00, equiprobable row-equiprobable column. IM, Initial matrix; 5 times, 5 times column merge network; 10 times, 10 times column merge network.

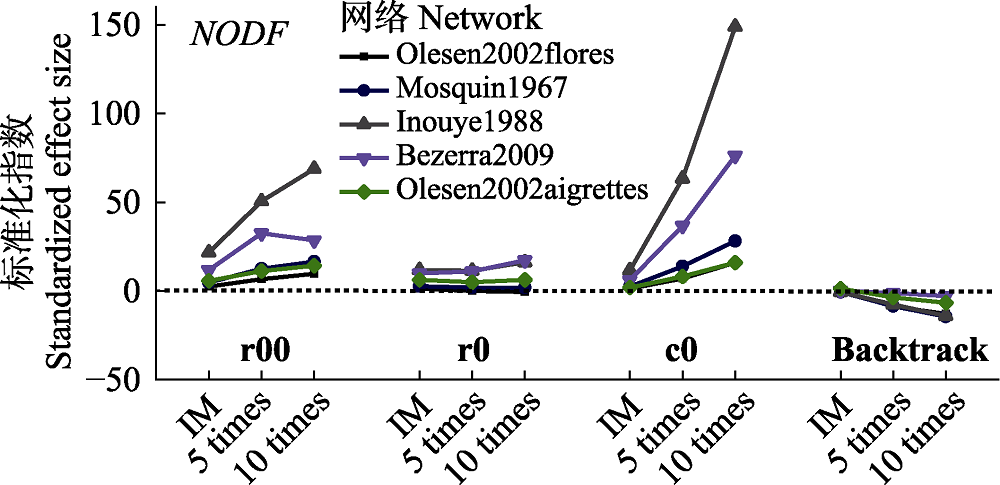
Fig. 6 Effects of matrix asymmetric variations o z-scores of on the standardized effect size (z-score) of nestedness metric based on overlap and decreasing fill (NODF). Backtrack, fixed row-fixed column; c0, equiprobable row-fixed column; r0, fixed row-equiprobable column; r00, equiprobable row- equiprobable column. IM, Initial matrix; 5 times, 5 times column merge network; 10 times, 10 times column merge network.

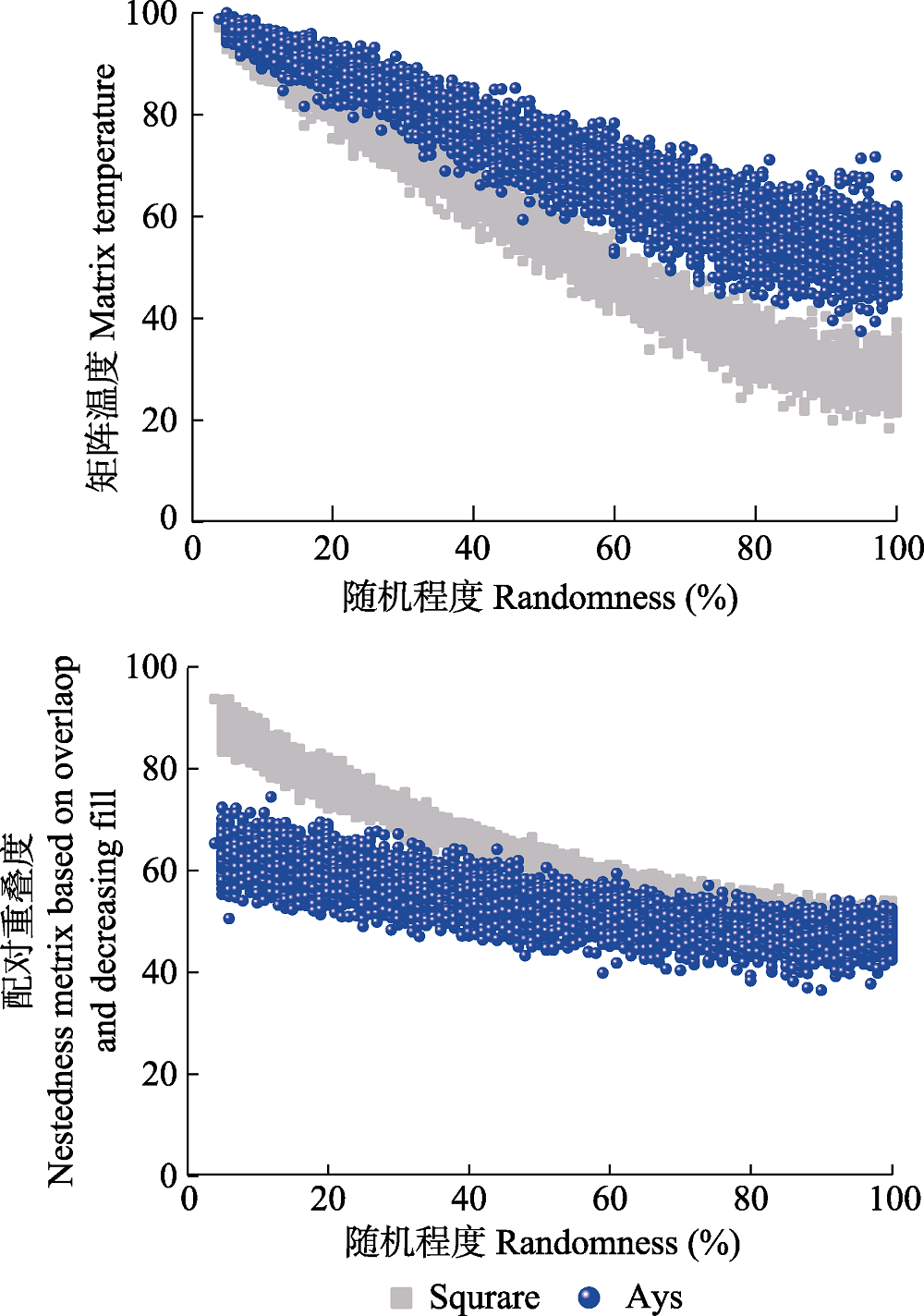
Fig. 7 Effects of the level of matrix randomness on nestedness metrics. Square, symmetric networks with rows and columns 30/30; Asy, asymmetric networks with rows and columns 5/55. Randomness, percentage of disordered cells deviates from fully nested matrix. Data contains a total of 4 850 matrices, with 4:100 (%) randomness degree 97 levels of, 50 repetitions per level.

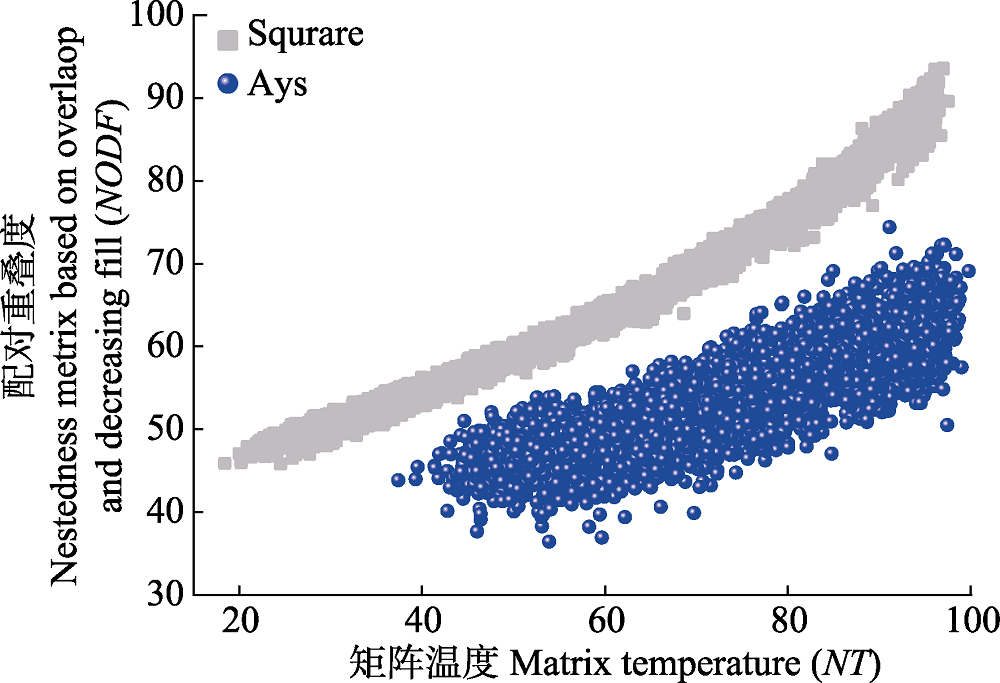
Fig. 8 Correlation between matrix temperature (NT) and nestedness metric based on overlap and decreasing fill (NODF). Square, symmetric networks with rows and columns 30/30; Asy, asymmetric networks with rows and columns 5/55. Randomness, percentage of disordered cells deviates from fully nested matrix. Data contains a total of 4 850 matrices, with 4:100 (%) randomness degree 97 levels of, 50 repetitions per level.

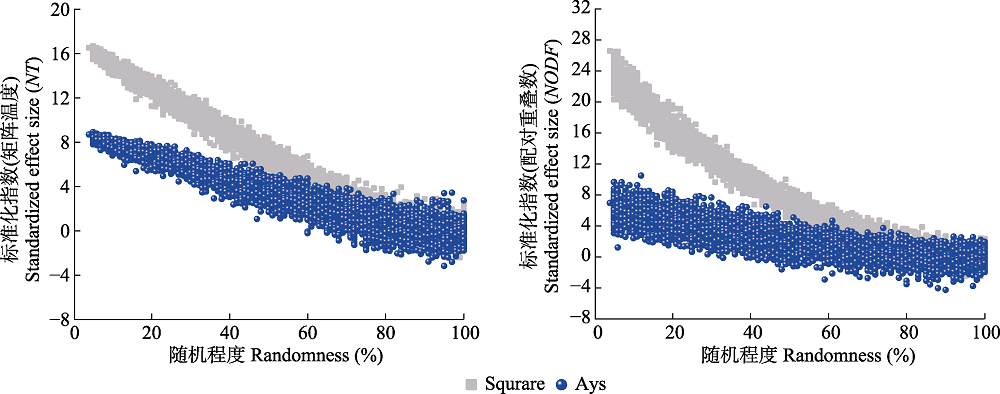
Fig. 9 Effects of the level of matrix randomness on the standardized effect size of nestedness. Square, symmetric networks with rows and columns 30/30; Asy, asymmetric networks with rows and columns 5/55. Randomness, percentage of disordered cells deviates from fully nested matrix. Data contains a total of 4 850 matrices, with 4:100 (%) random-ness degree 97 levels of, 50 repetitions per level. NT, matrix temperature; NODF, nestedness metric based on overlap and decreasing fill.

References 37

[1]	Almeida-Neto M, Guimarães P, Guimarães Jr PR, Loyola RD, Ulrich W ( 2008). A consistent metric for nestedness analysis in ecological systems: Reconciling concept and measurement. Oikos, 117, 1227-1239. DOI URL
[2]	Atmar W, Patterson BD ( 1993). The measure of order and disorder in the distribution of species in fragmented habitat. Oecologia, 96, 373-382. DOI URL PMID
[3]	Atmar W, Patterson BD ( 1995). The Nestedness Temperature Calculator: A Visual Basic Program, Including 294 Presence-absence Matrices. AICS Research, University Park, NM and Field Museum, Chicago.
[4]	Bahram M, Harend H, Tedersoo L ( 2014). Network perspectives of ectomycorrhizal associations. Fungal Ecology, 7, 70-77. DOI URL
[5]	Bahram M, Põlme S, Kõljalg U, Tedersoo L ( 2011). A single European aspen ( Populus tremula) tree individual may potentially harbour dozens of Cenococcum geophilum ITS genotypes and hundreds of species of ectomycorrhizal fungi. FEMS Microbiology Ecology, 75, 313-320. DOI URL PMID
[6]	Bascompte J ( 2010). Structure and dynamics of ecological networks. Science, 329, 765-766. DOI URL PMID
[7]	Bascompte J, Jordano P, Melian CJ, Olesen JM ( 2003). The nested assembly of plant-animal mutualistic networks. Proceedings of the National Academy of Sciences of the United States of America, 100, 9383-9387. DOI URL PMID
[8]	Beiler KJ, Simard SW, Durall DM ( 2015). Topology of tree-mycorrhizal fungus interaction networks in xeric and mesic Douglas-fir forests. Journal of Ecology, 103, 616-628. DOI URL
[9]	Bezerra ELS, Machado IC, Mello MAR ( 2009). Pollination networks of oil-flowers: A tiny world within the smallest of all worlds. Journal of Animal Ecology, 78, 1096-1101. DOI URL PMID
[10]	Blüthgen N, Menzel F, Hovestadt T, Fiala B, Blüthgen N ( 2007). Specialization, constraints, and conflicting interests in mutualistic networks. Current Biology, 17, 341-346. DOI URL PMID
[11]	Chagnon PL, U’Ren JM, Miadlikowska J, Lutzoni F, Elizabeth Arnold A ( 2016). Interaction type influences ecological network structure more than local abiotic conditions: Evidence from endophytic and endolichenic fungi at a continental scale. Oecologia, 180, 181-191. DOI URL PMID
[12]	Chen SH, Wang YJ ( 2004). Nestedness pattern of insular community assemblages and its applications. Chinese Journal of Ecology, 23, 81-87. URL PMID
	[ 陈水华, 王玉军 ( 2004). 岛屿群落组成的嵌套格局及其应用. 生态学杂志, 23, 81-87.] URL PMID
[13]	Cook RR, Quinn JF ( 1998). An evaluation of randomization models for nested species subsets analysis. Oecologia, 113, 584-592. DOI URL PMID
[14]	Dormann CF, Gruber B, Fruend J, Gruber B ( 2018). Bipartite: Analysis of bipartite ecological webs. R package version 2.11. .
[15]	Fang Q, Huang SQ ( 2012). Progress in pollination networks: Network structure and dynamics. Biodiversity Science, 20, 300-307. DOI URL
	[ 方强, 黄双全 ( 2012). 传粉网络的研究进展: 网络的结构和动态. 生物多样性, 20, 300-307.] DOI URL
[16]	Gao C, Zhang Y, Shi NN, Zheng Y, Chen L, Wubet T, Bruelheide H, Both S, Buscot F, Ding Q, Erfmeier A, Kühn P, Nadrowski K, Scholten T, Guo LD ( 2015). Community assembly of ectomycorrhizal fungi along a subtropical secondary forest succession. New Phytologist, 205, 771-785. DOI URL PMID
[17]	Gotelli NJ ( 2000). Null model analysis of species co-occurrence patterns. Ecology, 81, 2606-2621. DOI URL PMID
[18]	Inouye DW, Pyke GH ( 1988). Pollination biology in the Snowy Mountains of Australia: Comparisons with montane Colorado, USA. Australian Journal of Ecology, 13, 191-205.
[19]	Kennedy P, Nguyen NH, Cohen H, Peay K ( 2014). Missing checkerboards? An absence of competitive signal in Alnus-‌‌associated ectomycorrhizal fungal communities. Peer J, 2, e686. DOI: 10.7717/peerj.686. DOI URL PMID
[20]	Li ZC, Xu JY, Wu CY, Zhang Y ( 2011). A review of studies using ecological network analysis. Acta Ecologica Sinica, 31, 5396-5405.
	[ 李中才, 徐俊艳, 吴昌友, 张漪 ( 2011). 生态网络分析方法研究综述. 生态学报, 31, 5396-5405.]
[21]	Liu CR, Ma KP, Chen LZ ( 2002). Nestedness: Methods, mechanisms and implications for biological conservation. Acta Phytoecologica Sinica, 26, 68-72.
	[ 刘灿然, 马克平, 陈灵芝 ( 2002). 嵌套性: 研究方法、形成机制及其对生物保护的意义. 植物生态学报, 26, 68-72.]
[22]	Liu KL, Porras-Alfaro A, Kuske CR, Eichorst SA, Xie G ( 2012). Accurate, rapid taxonomic classification of fungal large-subunit rRNA genes. Applied and Environmental Microbiology, 78, 1523-1533. DOI URL PMID
[23]	Luo F, Pan Y, Lu CH ( 2013). Structural characteristics of plant-animal mutualistic networks and related affecting factors. Chinese Journal of Ecology, 32, 2179-2185.
	[ 罗芳, 潘扬, 鲁长虎 ( 2013). 动植物互惠网络结构及影响因素. 生态学杂志, 32, 2179-2185.]
[24]	Montesinos-Navarro A, Segarra-Moragues JG, Valiente-Banuet A, Verdú M ( 2012). The network structure of plant- arbuscular mycorrhizal fungi. New Phytologist, 194, 536-547. DOI URL PMID
[25]	Mosquin T, Martin JEH ( 1967). Observations on the pollination biology of plants on Melville Island, N.W.T, Canada. Canadian Field Naturalist, 81, 201-205.
[26]	Oksanen J, Blanchet FG, Friendly M, Kindt R, Legendre P, McGlinn D, Minchin PR, O’Hara RB, Simpson GL, Solymos P, Stevens MHH, Szoecs E, Wagner H ( 2019). Vegan: Community ecology package. R package version 2.5-4. . Cited: 2019-03-20 DOI URL PMID
[27]	Olesen JM, Eskildsen LI, Venkatasamy S ( 2002). Invasion of pollination networks on oceanic islands: Importance of invader complexes and endemic super generalists. Diversity and Distributions, 8, 181-192. DOI URL
[28]	Poisot T, Péquin B, Gravel D ( 2013). High-throughput sequencing: A roadmap toward community ecology. Ecology and Evolution, 3, 1125-1139. DOI URL PMID
[29]	Southworth D, He XH, Swenson W, Bledsoe CS, Horwath WR ( 2005). Application of network theory to potential mycorrhizal networks. Mycorrhiza, 15, 589-595. DOI URL PMID
[30]	Thebault E, Fontaine C ( 2010). Stability of ecological communities and the architecture of mutualistic and trophic networks. Science, 329, 853-856. DOI URL PMID
[31]	Toju H, Guimarães PR, Olesen JM, Thompson JN ( 2014). Assembly of complex plant-fungus networks. Nature Communications, 5, 5273. DOI: 10.1038/ncomms6273. DOI URL PMID
[32]	Ulrich W, Almeida-Neto M, Gotelli NJ ( 2009). A consumer’s guide to nestedness analysis. Oikos, 118, 3-17. DOI URL
[33]	Ulrich W, Gotelli NJ ( 2007). Null model analysis of species nestedness patterns. Ecology, 88, 1824-1831. DOI URL PMID
[34]	Ulrich W, Gotelli NJ ( 2013). Pattern detection in null model analysis. Oikos, 122, 2-18. DOI URL PMID
[35]	Vázquez DP, Blüthgen N, Cagnolo L, Chacoff NP ( 2009). Uniting pattern and process in plant-animal mutualistic networks: A review. Annals of Botany, 103, 1445-1457. DOI URL PMID
[36]	Wright DH, Patterson BD, Mikkelson GM, Cutler A, Atmar W ( 1997). A comparative analysis of nested subset patterns of species composition. Oecologia, 113, 1-20. DOI URL PMID
[37]	Zhang XM, Han XF, Liu LW, Xu AC ( 2016). Influencing factors of the nested distribution of butterfly assemblages in the Zhoushan Archipelago, China. Biodiversity Science, 24, 321-331. DOI URL
	[ 张雪梅, 韩徐芳, 刘立伟, 徐爱春 ( 2016). 舟山群岛蝶类群落嵌套分布格局及其影响因素. 生物多样性, 24, 321-331.] DOI URL