森林径级结构研究: 从统计描述到理论演绎

doi:10.17521/cjpe.2023.0301

摘要/Abstract

摘要：

森林径级结构是树木生长、竞争、死亡等过程的综合反映, 也是估算森林生物量、判断森林演替阶段与健康状态以及预测森林碳汇潜力的基础依据。林学领域早期对径级结构的研究以统计描述为主, 多采用常见的概率分布函数来拟合样地尺度上径级结构的动态变化, 缺乏对其形成机制的阐释。随着宏观生态学的发展, 最大熵原理、中心极限定理等被用于解释大尺度上发现的相对一致的森林径级结构, 但这类模型侧重概率统计, 对具体生态学过程的分析仍然欠缺。2000年以来, 在原始成熟森林中发现的径级结构的幂律特征催生了一系列理论研究, 包括代谢尺度理论、林窗演替理论等。这些理论尝试从树木个体大小和资源利用之间的关系, 以及树木对资源的竞争过程来演绎径级结构达到稳态时幂律特征的形成机制。种群统计平衡理论为稳态径级结构的分析提供了一般性框架, 揭示了不同的树木生长速率和死亡率如何导致径级结构特征的变化; 在此基础上, 种群统计最优性假设为径级结构的分析提供了新的视角。数学层面上, 转移矩阵、积分投影、偏微分方程等都是径级结构动力学分析的有力工具, 但由于这类数学模型的时间动态解析求解较为困难, 研究中通常预先假定森林处于理想的结构平衡状态。而在实际情况下, 结构非平衡往往是森林的常态, 也是森林碳库变化与碳汇潜力估算的基础。为了更好预测全球变化背景下的森林动态趋势, 应明确环境因子对径级相关的树木生长速率、死亡率的影响, 并发展径级结构动态特征的解析方法。

关键词: 森林径级结构, 资源竞争, 树木生长和死亡

Abstract:

Forest size structure (the diameter distribution of trees in a forest) is a comprehensive indicator of forest demographic processes. It is the basis for determining forest successional stage and the state of forest health, estimating forest biomass and predicting forest carbon sink potential. Studies of forest size structure began with statistical descriptions before progressing to theoretical and mathematical deduction. In early statistical studies of forestry, many common probability distribution functions were used to fit plot-scale variations in size structure, but most of these functions were not derived from biological processes and therefore lack clear biological meaning. With the development of macroecology, the principle of maximum entropy and the central limit theorem have been used to explain the relatively consistent forest size structure at large spatial scales. Such models mainly focus on probabilistic statistics rather than ecological processes. Reports of a power-law size structure in natural mature forests in the early 2000s spawned a series of theoretical studies, including metabolic scaling theory and the theory of gap succession, among others. These theories have proposed that the observed power-law size structure results from the relationship between tree size and resource use on the individual scale and tree competition for resources on the community scale. Demographic equilibrium theory provides a general framework for analyzing the relationship between the steady state forest size structure and tree growth and mortality. Under this equilibrium framework, the hypothesis of demographic optimality further provides a new perspective for the analysis of forest size structure. Mathematical models including transition matrices, integral projections, and partial differential equations are powerful tools for analyzing forest size structure dynamics. However, due to the difficulty of identifying time-varying solutions to the mathematical models, most studies have been confined to the framework of forest demographic equilibrium. To understand dynamic variations of forest size structure and predict forest carbon sink potential in a rapidly changing climate, it is essential both to find general time-varying solutions to the mathematical models and to tighten empirical constraints on the effects of climatic factors on forest growth and mortality rates.

Key words: forest size structure, resource competition, tree growth and mortality

周建, 王焓. 森林径级结构研究: 从统计描述到理论演绎. 植物生态学报, 2024, 48(6): 675-689. DOI: 10.17521/cjpe.2023.0301

ZHOU Jian, WANG Han. A review of forest size structure studies: from statistical description to theoretical deduction. Chinese Journal of Plant Ecology, 2024, 48(6): 675-689. DOI: 10.17521/cjpe.2023.0301

导出引用管理器 EndNote|Ris|BibTeX

链接本文: https://www.plant-ecology.com/CN/10.17521/cjpe.2023.0301

https://www.plant-ecology.com/CN/Y2024/V48/I6/675

图/表 4

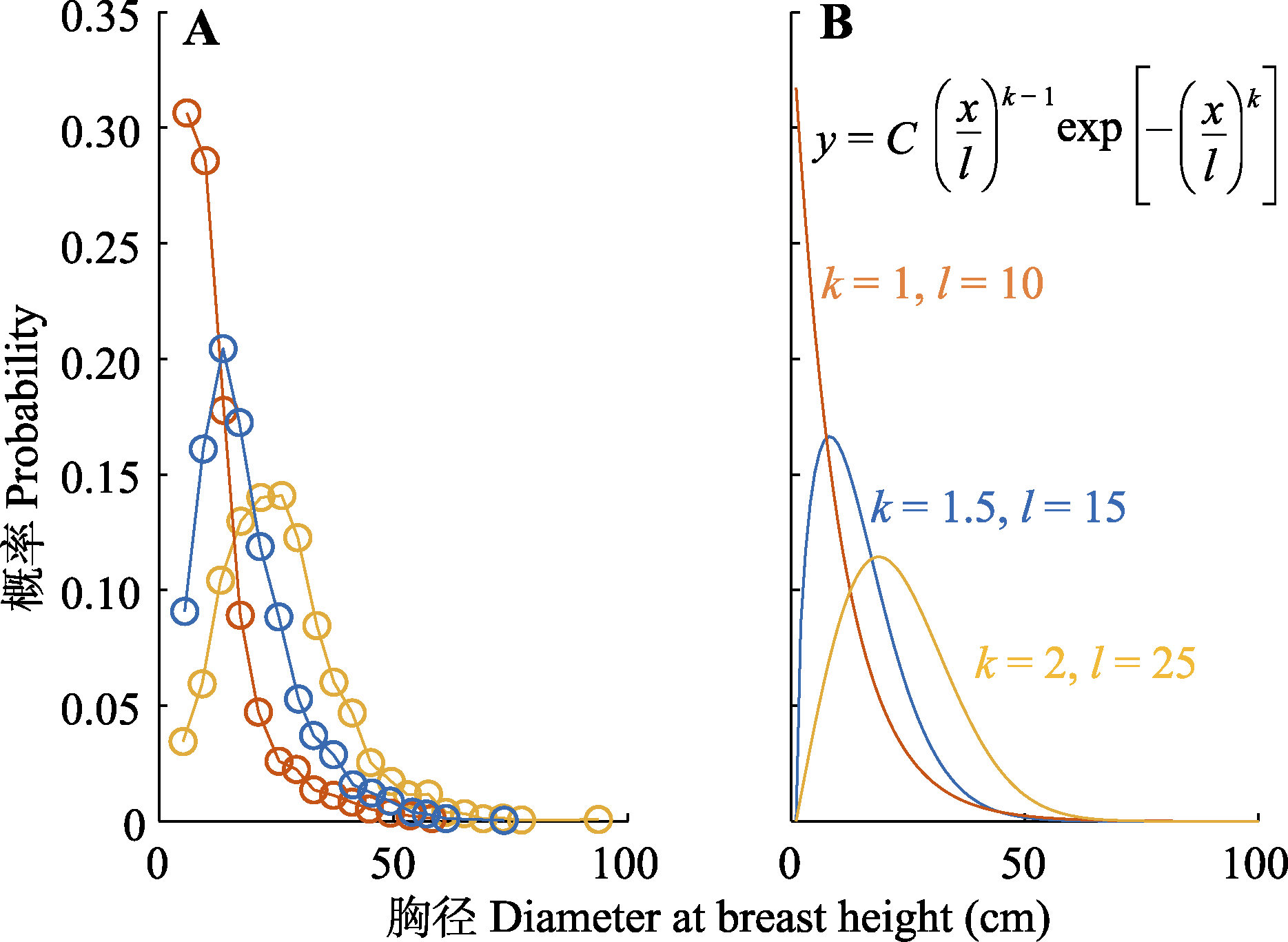
图1 Weibull分布在径级结构拟合中的应用。 A, 不同森林样地的径级结构示例(数据来自Coomes和Allen, 2007)。B, 双参数Weibull分布的不同参数取值对应的不同分布特征。C, 常数; k, 形状参数; l, 尺度参数。

Fig. 1 Application of Weibull distribution in studies of forest size structure. A, Different patterns of forest size structure in different forest plots (data from Coomes & Allen, 2007). B, Varying shape and scale parameters for the Weibull distribution leads to different patterns of the probability distribution function. C, constant value; k, shape parameter; l, scale parameter.

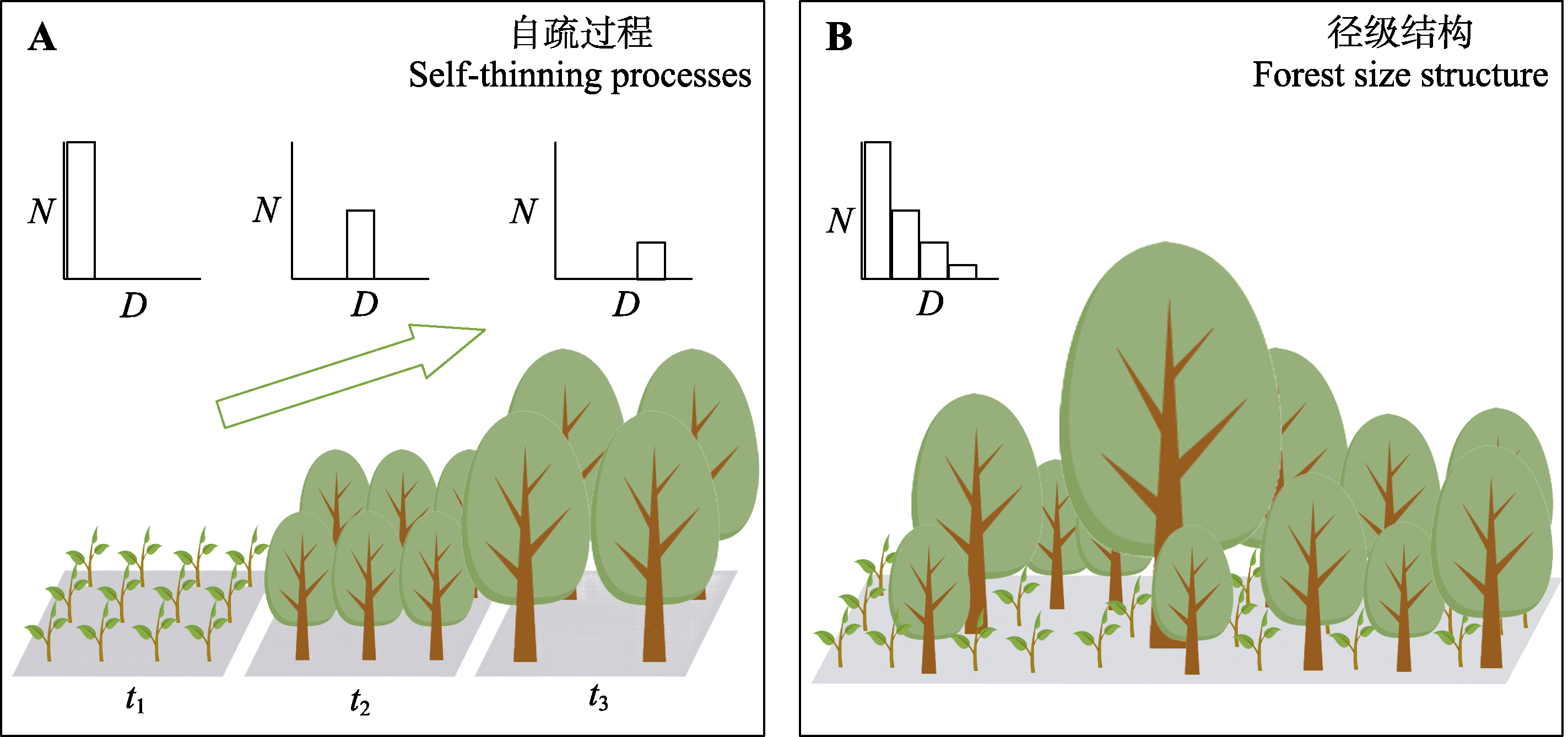
图2 同生群自疏过程中的个体大小数量关系(A)和大小个体混合的森林中的径级结构对比(B)。 t1、t2、t3代表自疏的不同阶段。D, 树木径级; N, 个体数量。

Fig. 2 Evolution of the size-density relationship associated with self-thinning in an even-sized cohort (A) and tree size structure in a mixed sized forest (B). t1, t2, t3 represent different stages of self-thinning. D, size class; N, individual number.

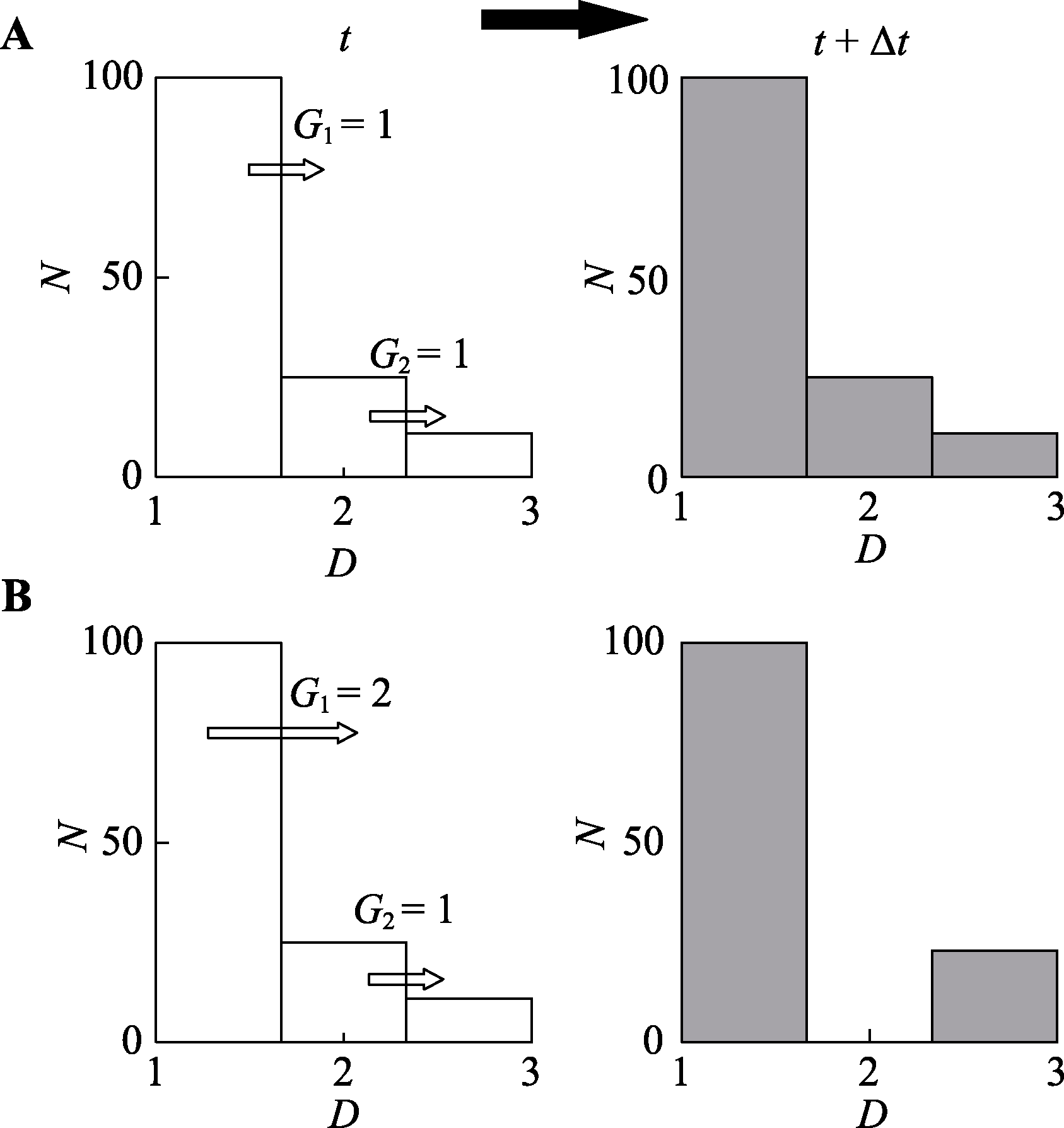
图3 各径级生长速率相同时径级结构不发生变化(A), 各径级生长速率不同时径级结构发生变化(B)。 D, 树木径级; N, 个体数量。G1、G2分别代表径级1、2的生长速率。

Fig. 3 Forest size structure remains constant when the same growth rate applies to each size class (A) and changes when the growth rate varies across different size classes (B). D, size class; N, individual number. G1 and G2 represent the growth rates of size class 1 and 2, respectively.

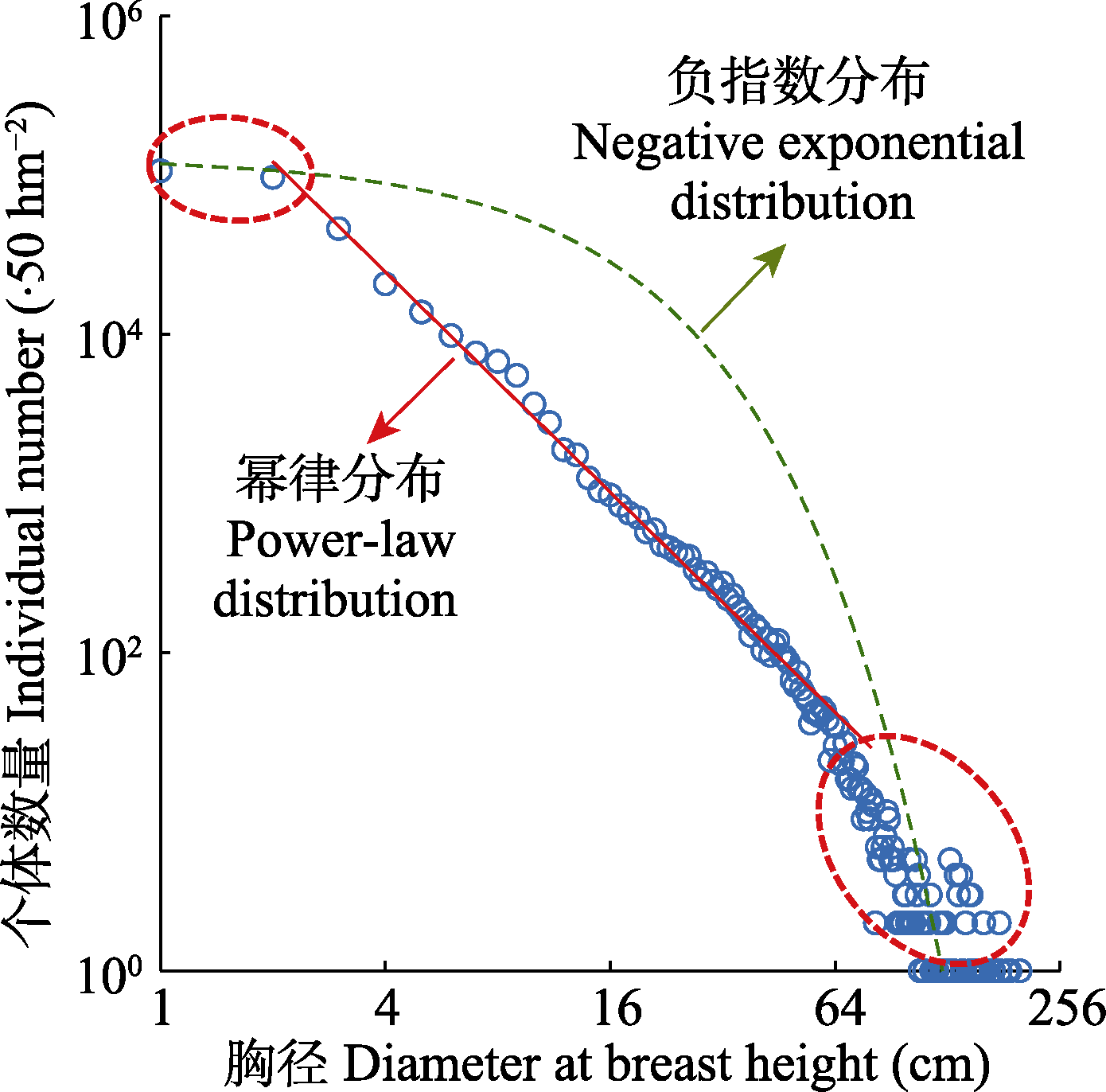
图4 巴罗科罗拉多岛(BCI) 50 hm2森林大样地2010年清查数据呈现的径级结构(蓝色圆圈): 中间部分符合幂律特征(红色直线), 头部和尾部偏离幂律特征(红色圆圈标记区域)。绿色虚线代表在恒定生长速率和死亡率条件下, 森林径级结构应该呈现的负指数分布特征。

Fig. 4 Forest size structure based on data from the Barro Colorado Island (BCI) 50 hm2 forest plot inventory in 2010 (blue circles): a power-law distribution at intermediate sizes (red solid line) breaks down in the head and tail (marked by red circles). Green dashed line shows a negative exponential distribution assuming constant growth rate and mortality.

参考文献 111

[1]	Acker SA, Boetsch JR, Bivin M, Whiteaker L, Cole C, Philippi T (2015). Recent tree mortality and recruitment in mature and old-growth forests in western Washington. Forest Ecology and Management, 336, 109-118.
[2]	Anderegg WRL, Hicke JA, Fisher RA, Allen CD, Aukema J, Bentz B, Hood S, Lichstein JW, Macalady AK, McDowell N, Pan YD, Raffa K, Sala AN, Shaw JD, Stephenson NL, et al. (2015). Tree mortality from drought, insects, and their interactions in a changing climate. New Phytologist, 208, 674-683. DOI PMID
[3]	Anju MV, Warrier RR, Kunhikannan C (2022). Significance of soil seed bank in forest vegetation: a review. Seeds, 1, 181-197.
[4]	Arthur WB (1981). Why a population converges to stability. The American Mathematical Monthly, 88, 557-563.
[5]	Bailey RL, Dell TR (1973). Quantifying diameter distributions with the Weibull function. Forest Science, 19, 97-104.
[6]	Banavar JR, Maritan A, Rinaldo A (1999). Size and form in efficient transportation networks. Nature, 399, 130-132.
[7]	Binkley D, Campoe OC, Gspaltl M, Forrester DI (2013). Light absorption and use efficiency in forests: Why patterns differ for trees and stands. Forest Ecology and Management, 288, 5-13.
[8]	Botkin DB, Janak JF, Wallis JR (1972). Some ecological consequences of a computer model of forest growth. Journal of Ecology, 60, 849-872.
[9]	Clauset A, Shalizi CR, Newman MEJ (2009). Power-law distributions in empirical data. Siam Review, 51, 661-703.
[10]	Condit R (1998). Tropical Forest Census Plots. Springer- Verlag, Berlin.
[11]	Coomes DA (2006). Challenges to the generality of WBE theory. Trends in Ecology & Evolution, 21, 593-596.
[12]	Coomes DA, Allen RB (2007). Mortality and tree-size distributions in natural mixed-age forests. Journal of Ecology, 95, 27-40.
[13]	Coomes DA, Allen RB (2009). Testing the Metabolic Scaling Theory of tree growth. Journal of Ecology, 97, 1369-1373.
[14]	Coomes DA, Duncan RP, Allen RB, Truscott J (2003). Disturbances prevent stem size-density distributions in natural forests from following scaling relationships. Ecology Letters, 6, 980-989.
[15]	Coulson T, Godfray HCJ (2007). Single-species dynamics//May R, McLean AR. Theoretical Ecology: Principles and Applications. Oxford University Press, Oxford. 17-34.
[16]	Cyr H, Walker SC (2004). An illusion of mechanistic understanding. Ecology, 85, 1802-1804.
[17]	Dalla Corte AP, Rex FE, Sanquetta CR, Silva CA, Moura MM, Wilkinson B, Zambrano AMA, da Cunha Neto EM, Veras HFP, de Moraes A, Klauberg C, Mohan M, Cardil A, Broadbent EN (2020). Measuring individual tree diameter and height using GatorEye high-density UAV-lidar in an integrated crop-livestock- forest system. Remote Sensing, 12, 863. DOI: 10.3390/rs12050863.
[18]	Damuth J (1981). Population density and body size in mammals. Nature, 290, 699-700.
[19]	Dassot M, Constant T, Fournier M (2011). The use of terrestrial LiDAR technology in forest science: application fields, benefits and challenges. Annals of Forest Science, 68, 959-974.
[20]	de Lima RAF, Batista JLF, Prado PI (2015). Modeling tree diameter distributions in natural forests: an evaluation of 10 statistical models. Forest Science, 61, 320-327.
[21]	Donato DC, Campbell JL, Franklin JF (2012). Multiple successional pathways and precocity in forest development: Can some forests be born complex? Journal of Vegetation Science, 23, 576-584.
[22]	Duncanson LI, Dubayah RO, Enquist BJ (2015). Assessing the general patterns of forest structure: quantifying tree and forest allometric scaling relationships in the United States. Global Ecology and Biogeography, 24, 1465-1475.
[23]	Dybzinski R, Farrior C, Wolf A, Reich PB, Pacala SW (2011). Evolutionarily stable strategy carbon allocation to foliage, wood, and fine roots in trees competing for light and nitrogen: an analytically tractable, individual-based model and quantitative comparisons to data. The American Naturalist, 177, 153-166. DOI PMID
[24]	Easterling MR, Ellner SP, Dixon PM (2000). Size-specific sensitivity: applying a new structured population model. Ecology, 81, 694-708.
[25]	Ebenman B, Persson L (1988). Size-Structured Populations: Ecology and Evolution. Springer-Verlag, Berlin.
[26]	Ellner SP, Rees M (2006). Integral projection models for species with complex demography. The American Naturalist, 167, 410-428. PMID
[27]	Enquist BJ, Brown JH, West GB (1998). Allometric scaling of plant energetics and population density. Nature, 395, 163-165.
[28]	Enquist BJ, Niklas KJ (2001). Invariant scaling relations across tree-dominated communities. Nature, 410, 655-660.
[29]	Enquist BJ, West GB, Brown JH (2009). Extensions and evaluations of a general quantitative theory of forest structure and dynamics. Proceedings of the National Academy of Sciences of the United States of America, 106, 7046-7051.
[30]	Ercanlı İ (2020). Innovative deep learning artificial intelligence applications for predicting relationships between individual tree height and diameter at breast height. Forest Ecosystems, 7, 12. DOI: 10.1186/s40663-020-00226-3.
[31]	Farrior CE, Bohlman SA, Hubbell S, Pacala SW (2016). Dominance of the suppressed: power-law size structure in tropical forests. Science, 351, 155-157. DOI PMID
[32]	Fisher RA, Koven CD (2020). Perspectives on the future of land surface models and the challenges of representing complex terrestrial systems. Journal of Advances in Modeling Earth Systems, 12, e2018MS001453. DOI: 10.1029/2018MS001453.
[33]	Ford ED (1975). Competition and stand structure in some even-aged plant monocultures. Journal of Ecology, 63, 311-333.
[34]	Forrester DI, Limousin JM, Pfautsch S (2022). The relationship between tree size and tree water-use: Is competition for water size-symmetric or size-asymmetric? Tree Physiology, 42, 1916-1927. DOI PMID
[35]	Frank SA (2016). The invariances of power law size distributions. F1000Research, 5, 2074. DOI: 10.12688/f1000research.9452.3. PMID
[36]	Han WX, Fang JY (2003). Allometry and its application in ecological scaling. Acta Scicentiarum Naturalum Universitis Pekinesis, 39, 583-593.
	[韩文轩, 方精云 (2003). 相关生长关系与生态学研究中的尺度转换. 北京大学学报(自然科学版), 39, 583-593.]
[37]	Hara T (1984). A stochastic model and the moment dynamics of the growth and size distribution in plant populations. Journal of Theoretical Biology, 109, 173-190.
[38]	Hara T (1988). Dynamics of size structure in plant populations. Trends in Ecology & Evolution, 3, 129-133.
[39]	Harrison SP, Cramer W, Franklin O, Prentice IC, Wang H, Brännström Å, de Boer H, Dieckmann U, Joshi J, Keenan TF, Lavergne A, Manzoni S, Mengoli G, Morfopoulos C, Peñuelas J, et al. (2021). Eco-evolutionary optimality as a means to improve vegetation and land-surface models. New Phytologist, 231, 2125-2141. DOI PMID
[40]	Harte J (2011). Maximum Entropy and Ecology: a Theory of Abundance, Distribution, and Energetics. Oxford University Press, Oxford.
[41]	Harte J, Zillio T, Conlisk E, Smith AB (2008). Maximum entropy and the state-variable approach to macroecology. Ecology, 89, 2700-2711. DOI PMID
[42]	Hong LX, Du GJ, Zhang QR, Liu BT (1995). Weibull distribution and dynamic prediction of DBH in natural evergreen broad-leaved young forest with different ages. Chinese Journal of Plant Ecology, 19, 29-42.
	[洪利兴, 杜国坚, 张庆荣, 刘本同 (1995). 天然常绿阔叶异龄幼林胸径的Weibull分布及动态预测. 植物生态学报, 19, 29-42.]
[43]	Hou JH, Huang JH, Ma KP (2004). Eleven-year population growth dynamics of major species in a Quercus liaotungensis forest in the Dongling Mountains, northern China. Acta Phytoecologica Sinica, 28, 609-615.
	[侯继华, 黄建辉, 马克平 (2004). 东灵山辽东栎林主要树种种群11年动态变化. 植物生态学报, 28, 609-615.] DOI
[44]	Hubbell SP, Condit R, Foster RB (2005). Barro Colorado Forest Census Plot Data. [2023-10- 23]. http://ctfs.si.edu/webatlas/datasets/bci .
[45]	Hubbell SP, Foster RB, O’Brien ST, Harms KE, Condit R, Wechsler B, Wright SJ, de Lao SL (1999). Light-Gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science, 283, 554-557. DOI PMID
[46]	Hui GY, Sheng WT (1995). Study on stand diameter structure model. Forest Research, 8(2), 127-131.
	[惠刚盈, 盛炜彤 (1995). 林分直径结构模型的研究. 林业科学研究, 8(2), 127-131.]
[47]	Iida Y, Poorter L, Sterck F, Kassim AR, Potts MD, Kubo T, Kohyama TS (2014). Linking size-dependent growth and mortality with architectural traits across 145 co-occurring tropical tree species. Ecology, 95, 353-363. PMID
[48]	Jaynes ET (1957a). Information theory and statistical mechanics. Physical Review, 106, 620-630.
[49]	Jaynes ET (1957b). Information theory and statistical mechanics. II. Physical Review, 108, 171-190.
[50]	Kankare V, Liang X, Vastaranta M, Yu X, Holopainen M, Hyyppä J (2015). Diameter distribution estimation with laser scanning based multisource single tree inventory. ISPRS Journal of Photogrammetry and Remote Sensing, 108, 161-171.
[51]	Knox RG, Peet RK, Christensen NL (1989). Population dynamics in loblolly pine stands: changes in skewness and size inequality. Ecology, 70, 1153-1167.
[52]	Kohyama T, Hara T (1989). Frequency distribution of tree growth rate in natural forest stands. Annals of Botany, 64, 47-57.
[53]	Kolmogoroff A (1931). Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung. Mathematische Annalen, 104, 415-458.
[54]	Kou WZ (1982). A study of the distribution of diameter of wood. Journal of Nanjing Forestry University (Natural Sciences Edition), 6(1), 51-65.
	[寇文正 (1982). 林木直径分布的研究. 南京林业大学学报(自然科学版), 6(1), 51-65.] DOI
[55]	Kozłowski J, Konarzewski M (2004). Is West, Brown and Enquist’s model of allometric scaling mathematically correct and biologically relevant? Functional Ecology, 18, 283-289.
[56]	Kunstler G, Lavergne S, Courbaud B, Thuiller W, Vieilledent G, Zimmermann NE, Kattge J, Coomes DA (2012). Competitive interactions between forest trees are driven by species’ trait hierarchy, not phylogenetic or functional similarity: implications for forest community assembly. Ecology Letters, 15, 831-840. DOI PMID
[57]	Lee ED, Kempes CP, West GB (2021). Growth, death, and resource competition in sessile organisms. Proceedings of the National Academy of Sciences of the United States of America, 118, e2020424118. DOI: 10.1073/pnas.2020424118.
[58]	Leslie PH (1945). On the use of matrices in certain population mathematics. Biometrika, 33, 183-212. PMID
[59]	Li RW, Qin ZG, Pan P, Zhu ZF (2000). Diameter distribution of plantations of Eucommia uimoides. Journal of Sichuan Forestry Science and Technology, 21(2), 1-6.
	[李荣伟, 覃志刚, 潘攀, 朱志芳 (2000). 杜仲人工林林分直径分布研究. 四川林业科技, 21(2), 1-6.]
[60]	Liang J, Picard N (2013). Matrix model of forest dynamics: an overview and outlook. Forest Science, 59, 359-378.
[61]	Liu Z, Peng C, Work T, Candau JN, DesRochers A, Kneeshaw D (2018). Application of machine-learning methods in forest ecology: recent progress and future challenges. Environmental Reviews, 26, 339-350.
[62]	Losos EC, Leigh EG (2004). Forest Diversity and Dynamism: Findings from a Network of Large-scale Tropical Forest Plots. University of Chicago Press, Chicago.
[63]	Marquet PA, Quiñones RA, Abades S, Labra F, Tognelli M, Arim M, Rivadeneira M (2005). Scaling and power-laws in ecological systems. Journal of Experimental Biology, 208, 1749-1769. PMID
[64]	Martínez Cano I, Shevliakova E, Malyshev S, Wright SJ, Detto M, Pacala SW, Muller-Landau HC (2020). Allometric constraints and competition enable the simulation of size structure and carbon fluxes in a dynamic vegetation model of tropical forests (LM3PPA-TV). Global Change Biology, 26, 4478-4494.
[65]	McDowell NG, Allen CD, Anderson-Teixeira K, Aukema BH, Bond-Lamberty B, Chini L, Clark JS, Dietze M, Grossiord C, Hanbury-Brown A, Hurtt GC, Jackson RB, Johnson DJ, Kueppers L, Lichstein JW, et al. (2020). Pervasive shifts in forest dynamics in a changing world. Science, 368, eaaz9463. DOI: 10.1126/science.aaz9463.
[66]	Meng XY (2006). Forest Mensuration. 3rd ed. China Forestry Publishing House, Beijing.
	[孟宪宇 (2006). 测树学. 3版. 中国林业出版社, 北京.]
[67]	Meyer HA (1952). Structure, growth, and drain in balanced uneven-aged forests. Journal of Forestry, 50, 85-92.
[68]	Meyer WH (1930). Diameter distribution series in even-aged forest stands. Yale School of Forestry Bulletin, 28, 105.
[69]	Michaletz ST, Cheng D, Kerkhoff AJ, Enquist BJ (2014). Convergence of terrestrial plant production across global climate gradients. Nature, 512, 39-43.
[70]	Moorcroft PR, Hurtt GC, Pacala SW (2001). A method for scaling vegetation dynamics: the ecosystem demography model (ED). Ecological Monographs, 71, 557-585.
[71]	Moore J, Argles A, Cox P (2023). A theory of demographic optimality in forests. Scientific Reports, 13, 18712. DOI: 10.5194/bg-17-1013-2020.
[72]	Muller-Landau HC, Condit RS, Harms KE, Marks CO, Thomas SC, Bunyavejchewin S, Chuyong G, Co L, Davies S, Foster R, Gunatilleke S, Gunatilleke N, Hart T, Hubbell SP, Itoh A, et al. (2006). Comparing tropical forest tree size distributions with the predictions of metabolic ecology and equilibrium models. Ecology Letters, 9, 589-602. PMID
[73]	Newman M (2005). Power laws, Pareto distributions and Zipf’s law. Contemporary Physics, 46, 323-351.
[74]	Niklas KJ, Enquist BJ (2001). Invariant scaling relationships for interspecific plant biomass production rates and body size. Proceedings of the National Academy of Sciences of the United States of America, 98, 2922-2927. DOI PMID
[75]	Oizumi R, Takada T (2013). Optimal life schedule with stochastic growth in age-size structured models: theory and an application. Journal of Theoretical Biology, 323, 76-89. DOI PMID
[76]	Okubo A, Hastings A, Powell T (2001). Population dynamics in temporal and spatial domains//Okubo A, Levin SA. Diffusion and Ecological Problems: Modern Perspectives. Springer, New York.
[77]	Pan Y, Birdsey RA, Fang J, Houghton R, Kauppi PE, Kurz WA, Phillips OL, Shvidenko A, Lewis SL, Canadell JG, Ciais P, Jackson RB, Pacala SW, McGuire AD, Piao S, et al. (2011). A large and persistent carbon sink in the world’s forests. Science, 333, 988-993.
[78]	Phillips SJ, Anderson RP, Schapire RE (2006) Maximum entropy modeling of species geographic distributions. Ecological Modelling, 190, 231-259.
[79]	Phillips SJ, Dudík M (2008). Modeling of species distributions with MaxEnt: new extensions and a comprehensive evaluation. Ecography, 31, 161-175.
[80]	Piotto D (2008). A meta-analysis comparing tree growth in monocultures and mixed plantations. Forest Ecology and Management, 255, 781-786.
[81]	Pretzsch H (2009). Forest Dynamics, Growth and Yield: from Measurement to Model. Springer-Verlag, Berlin, Germany.
[82]	Reineke LH (1933). Perfecting a stand-density index for even-aged forests. Journal of Agricultural Research, 46, 627-638.
[83]	Salehnasab A, Bayat M, Namiranian M, Khaleghi B, Omid M, Masood Awan HU, Al-Ansari N, Jaafari A (2022). Machine learning for the estimation of diameter increment in mixed and uneven-aged forests. Sustainability, 14, 3386. DOI: 10.3390/su14063386.
[84]	Shipley B, Vile D, Garnier E (2006). From plant traits to plant communities: a statistical mechanistic approach to biodiversity. Science, 314, 812-814. PMID
[85]	Strigul N, Pristinski D, Purves D, Dushoff J, Pacala S (2008). Scaling from trees to forests: tractable macroscopic equations for forest dynamics. Ecological Monographs, 78, 523-545.
[86]	Sun SC, Cao QV, Cao TJ (2019). Characterizing diameter distributions for uneven-aged pine-oak mixed forests in the Qinling Mountains of China. Forests, 10, 596. DOI: 10.3390/f10070596.
[87]	Usher M (1969). A matrix model for forest management. Biometrics, 309-315.
[88]	Volkov I, Banavar JR, Hubbell SP, Maritan A (2009). Inferring species interactions in tropical forests. Proceedings of the National Academy of Sciences of the United States of America, 106, 13854-13859. DOI PMID
[89]	von Foerster H (1959). Some remarks on changing populations//Stohlman Jr F. The Kinetics of Cellular Proliferation. Grune and Stratton, New York. 382-407.
[90]	Wang M, Rennolls K (2005). Tree diameter distribution modelling: introducing the logit logistic distribution. Canadian Journal of Forest Research, 35, 1305-1313.
[91]	Wang ML, Sun DZ (1998). Quantifying and predicting stand diameter structure with the logistic distribution. Forest Research, 11, 537-541.
	[王明亮, 孙德宙 (1998). Logistic分布预测林分直径结构的研究. 林业科学研究, 11, 537-541.]
[92]	Weibull W (1951). A statistical distribution function of wide applicability. Journal of Applied Mechanics, 18, 293-297.
[93]	Weiner J (1990). Asymmetric competition in plant populations. Trends in Ecology & Evolution, 5, 360-364.
[94]	Weiner J, Thomas SC (1986). Size variability and competition in plant monocultures. Oikos, 47, 211-222.
[95]	Weng ES, Aleinov I, Singh R, Puma MJ, McDermid SS, Kiang NY, Kelley M, Wilcox K, Dybzinski R, Farrior CE, Pacala SW, Cook BI (2022). Modeling demographic-driven vegetation dynamics and ecosystem biogeochemical cycling in NASA GISS’s Earth system model (ModelE- BiomeE v.1.0). Geoscientific Model Development, 15, 8153-8180.
[96]	Weng ES, Farrior CE, Dybzinski R, Pacala SW (2017). Predicting vegetation type through physiological and environmental interactions with leaf traits: evergreen and deciduous forests in an earth system modeling framework. Global Change Biology, 23, 2482-2498. DOI PMID
[97]	West GB, Brown JH, Enquist BJ (1997). A general model for the origin of allometric scaling laws in biology. Science, 276, 122-126.
[98]	West GB, Brown JH, Enquist BJ (1999). A general model for the structure and allometry of plant vascular systems. Nature, 400, 664-667.
[99]	West GB, Enquist BJ, Brown JH (2009). A general quantitative theory of forest structure and dynamics. Proceedings of the National Academy of Sciences of the United States of America, 106, 7040-7045.
[100]	White EP, Enquist BJ, Green JL (2008). On estimating the exponent of power-law frequency distributions. Ecology, 89, 905-912.
[101]	White EP, Ernest SK, Kerkhoff AJ, Enquist BJ (2007). Relationships between body size and abundance in ecology. Trends in Ecology & Evolution, 22, 323-330.
[102]	Xiao X, McGlinn DJ, White EP (2015). A strong test of the maximum entropy theory of ecology. The American Naturalist, 185, E70-E80.
[103]	Xing DL, Hao ZQ (2011). The principle of maximum entropy and its applications in ecology. Biodiversity Science, 19, 295-302.
	[邢丁亮, 郝占庆 (2011). 最大熵原理及其在生态学研究中的应用. 生物多样性, 19, 295-302.] DOI
[104]	Yuan CM, Yang GP, Geng YF, Zhang SS (2022). Prediction of population dynamics of the endangered plant Pterospermum kingtungense using integral projection models. Ecology and Environmental Sciences, 31, 1530-1536.
	[袁春明, 杨国平, 耿云芬, 张珊珊 (2022). 基于积分投影模型预测濒危植物景东翅子树的种群动态. 生态环境学报, 31, 1530-1536.] DOI
[105]	Zhang Z, Cao L, Mulverhill C, Liu H, Pang Y, Li Z (2019). Prediction of diameter distributions with multimodal models using LiDAR data in subtropical planted forests. Forests, 10, 125. DOI: 10.3390/f10020125.
[106]	Zhou J (2018). Unsteady State Solutions for Two Diffusion Processes and Their Ecological Significances. PhD dissertation, Tsinghua University, Beijing. 36-40.
	[周建 (2018). 两类扩散过程的非稳态解及其生态学意义. 博士学位论文, 清华大学, 北京. 36-40.]
[107]	Zhou J (2023). Demographic disequilibrium and growth- mortality asymmetry of forests across climate gradients. bioRxiv, 259298073. DOI: 10.1101/2023.06.25.546473.
[108]	Zhou J, Lin GH (2018). Will forest size structure follow the-2 power-law distribution under ideal demographic equilibrium state? Journal of Theoretical Biology, 452, 17-21.
[109]	Zhou J, Yu KL, Lin GH, Wang ZH (2021). Variance in tree growth rates provides a key link for completing the theory of forest size structure formation. Journal of Theoretical Biology, 529, 110857. DOI: 10.1016/j.jtbi.2021.110857.
[110]	Zianis D, Mencuccini M (2004). On simplifying allometric analyses of forest biomass. Forest Ecology and Management, 187, 311-332.
[111]	Zuidema PA, Jongejans E, Chien PD, During HJ, Schieving F (2010). Integral Projection Models for trees: a new parameterization method and a validation of model output. Journal of Ecology, 98, 345-355.