

植物生态学报 ›› 2013, Vol. 37 ›› Issue (11): 1059-1070.DOI: 10.3724/SP.J.1258.2013.00109
所属专题: 生态系统结构与功能
• 综述 • 上一篇
收稿日期:2013-08-05
接受日期:2013-09-29
出版日期:2013-08-05
发布日期:2013-11-06
通讯作者:
于德永
基金资助:
SUN Yun,YU De-Yong( ),LIU Yu-Peng,HAO Rui-Fang
),LIU Yu-Peng,HAO Rui-Fang
Received:2013-08-05
Accepted:2013-09-29
Online:2013-08-05
Published:2013-11-06
Contact:
YU De-Yong
摘要:
当一个存在多稳态的生态系统临近突变阈值点时, 外界条件即使发生一个微小变化, 也会引发生态系统的剧烈响应, 使之进入结构和功能截然不同的另一稳定状态, 这种现象称为重大突变(critical transition)。重大突变所导致的稳态转换总是伴随着生态系统服务的急剧变化, 可能对人类可持续发展产生重大影响。预测生态系统突变的发生非常困难, 但科学家在此领域的大量研究结果表明, 通过监测一些通用指标可以判断生态系统是否不断临近重大突变阈值点, 进而可以进行生态系统重大突变预警。该文对近年来生态系统重大突变检测领域所取得的成果进行总结与归纳, 论述了生态系统重大突变的产生机制及其后果, 介绍了生态系统突变预警信号提取的理论基础, 从时间和空间两个维度总结了近年来生态系统重大突变预警信号的提取方法, 概述了当前研究面临的挑战, 指出生态系统突变预警信号的检测应充分利用时空动态数据, 并且联合多个指标, 从多个角度进行综合预警, 此外, 还应重视生态系统结构与重大突变之间的关系, 增强生态系统突变预警能力。
孙云,于德永,刘宇鹏,郝蕊芳. 生态系统重大突变检测研究进展. 植物生态学报, 2013, 37(11): 1059-1070. DOI: 10.3724/SP.J.1258.2013.00109
SUN Yun,YU De-Yong,LIU Yu-Peng,HAO Rui-Fang. Review on detection of critical transition in ecosystems. Chinese Journal of Plant Ecology, 2013, 37(11): 1059-1070. DOI: 10.3724/SP.J.1258.2013.00109
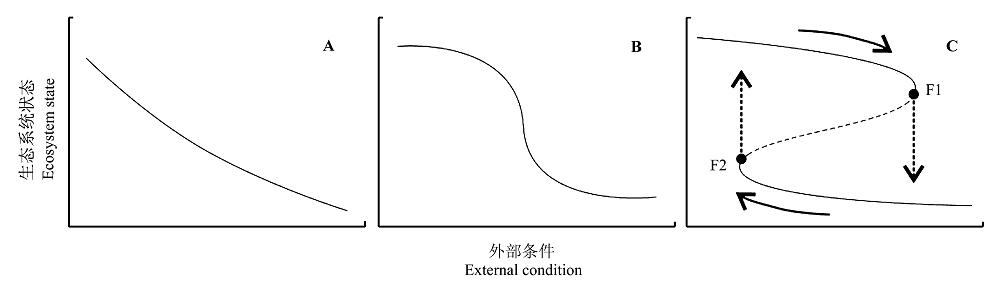
图1 生态系统对外部条件变化的不同响应方式。A, 生态系统状态与外部条件之间的响应函数曲线是光滑且连续的。B, 当外部条件达到某一水平时, 生态系统状态发生剧烈变化。C, 在一定的外部条件下生态系统有两个稳态, F1和F2是生态系统突变点。(引自Scheffer & Carpenter, 2003)
Fig. 1 Different responses of an ecosystem to changes in external conditions. A, Response function curve is smooth and continuous between ecosystem state and external conditions. B, Ecosystem changes profoundly when external conditions approach a critical level. C, Ecosystem has two stable states over a range of conditions. F1 and F2 are transition points of ecosystem. (Cited from Scheffer & Carpenter, 2003)
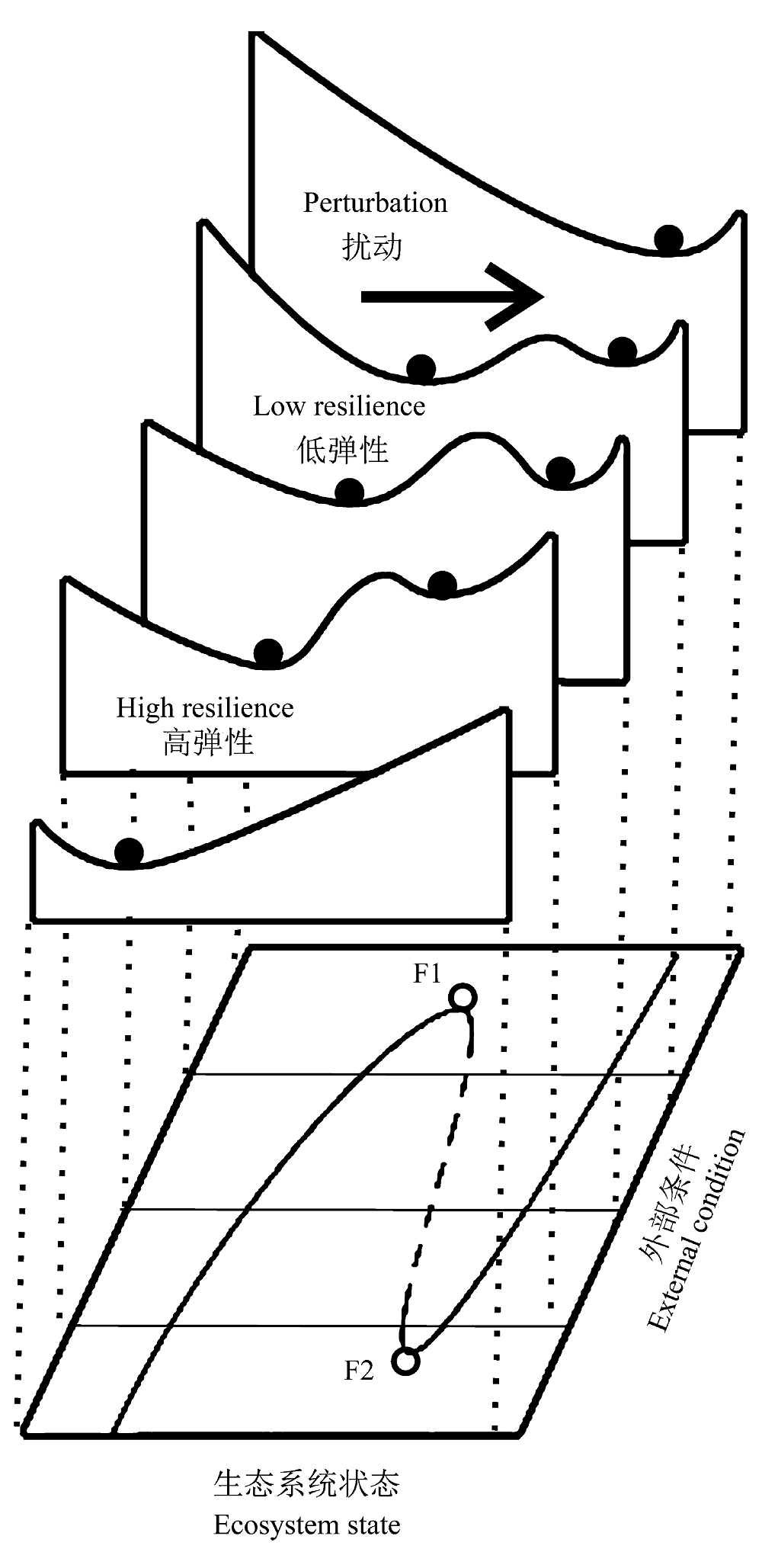
图2 外部条件对生态系统弹性的影响。F1和F2是生态系统突变点。(引自Scheffer et al., 2001)
Fig. 2 Effects of external conditions on ecological resilience. F1 and F2 are transition points of ecosystem. (Cited from Scheffer et al., 2001)
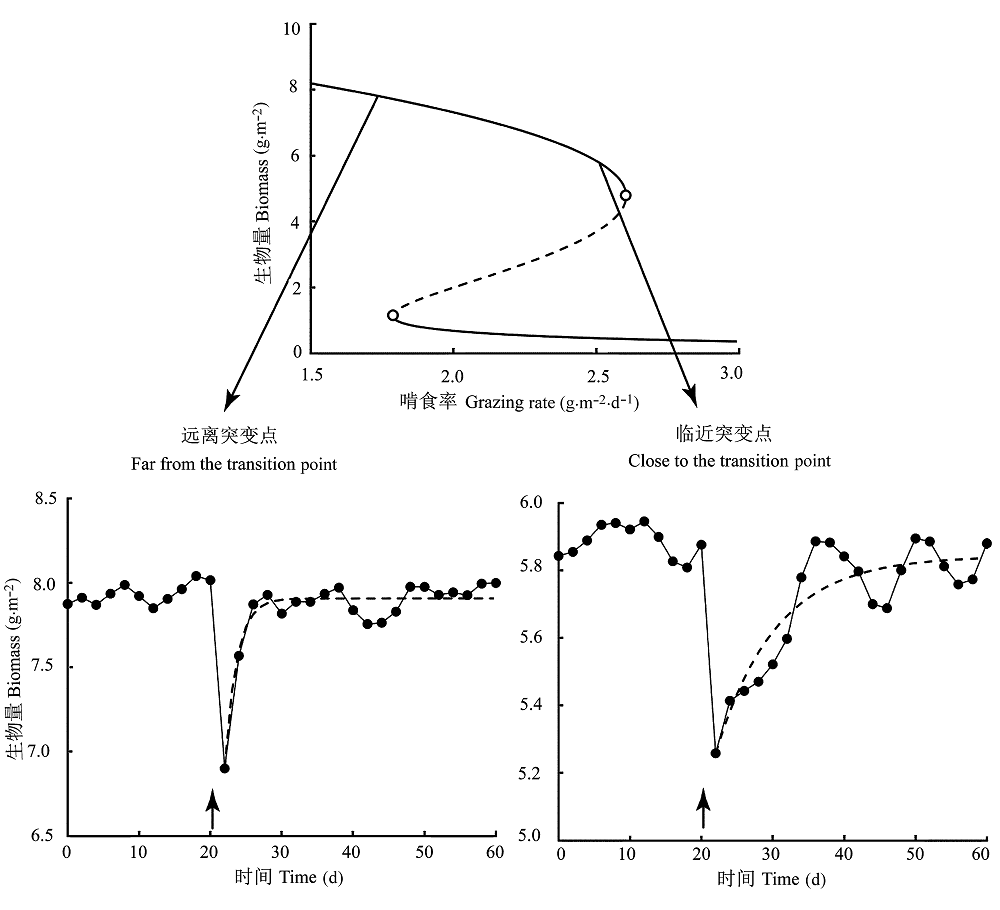
图3 不同情形下生态系统经历扰动后的恢复能力。(引自van Nes & Scheffer, 2007)
Fig. 3 Recovery ability of ecosystem following perturbation under different circumstances. (Cited from van Nes & Scheffer, 2007)
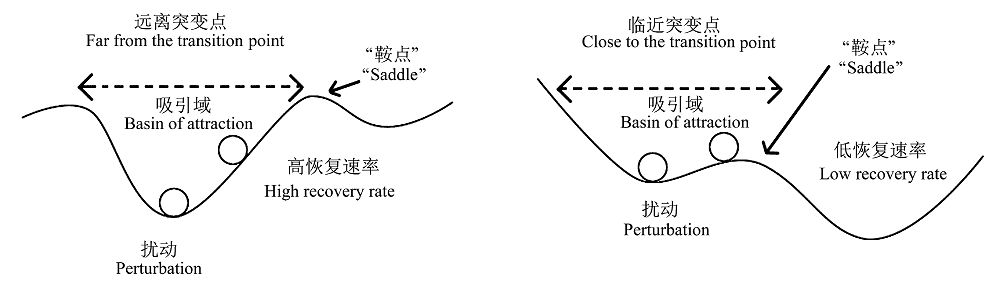
图4 不同情形下生态系统稳定性景观。(Synergy Program for Analyzing Resilience and Critical Transitions, 2012)
Fig. 4 Ecologically stable landscape under different circumstances. (Synergy Program for Analyzing Resilience and Critical Transitions, 2012)
| 主要突变检测方法 Key methods of detecting critical transition | 主要内容 Main contents | 计算公式 Formula | 局限性 Limitation |
|---|---|---|---|
| 测量恢复时间 Measuring the recovery time | 直接测量系统遭受微小事件扰动时恢复到最初平衡态的时间 Directly measuring the recovery time to equilibrium after a small perturbation | 适用于模拟试验, 对现实生态系统可操作性差 Suitable to simulation experiments, but not feasible in reality | |
| 计算自相关系数、方差, 功率谱分析 Computing autocorrelation and variance, and performing power spectrum analysis | 计算指示系统状态的变量的自相关系数、方差, 对时间序列进行功率谱分析 Computing autocorrelation and variance of the variables that indicate the status of the ecosystem, and analyzing the power spectrum of the time series | $\rho =\frac{E[(\mathop{z}_{t}-\mu )(\mathop{z}_{t+1}-\mu )]}{{}^{\mathop{\mathop{s}_{z}}^{2}}}$ | 数据获取困难和数据处理过程带入的误差和主观性 Difficult to acquire data; error and subjectivity are easily brought to the processing |
| $\mathop{s}^{2}=\frac{1}{n}\sum\limits_{t=1}^{n}{\mathop{(\mathop{z}_{t}-\mu )}^{2}}$ | |||
| μ和sz2分别表示状态变量zt的平均值和方差 μ and sz2 represent the average and variance of zt, respectively | |||
| 计算偏度 Computing the skewness | 由一个描述系统状态变量的时间序列数据计算出偏度绝对值 Computing the absolute value of skewness from the time series of variables that indicate ecosystem state | $\mathop{s}_{k}=\frac{\frac{1}{n}\sum\limits_{t=1}^{n}{\mathop{(\mathop{z}_{t}-\mu )}^{3}}}{\sqrt{\frac{1}{n}\sum\limits_{t=1}^{n}{\mathop{(\mathop{z}_{t}-\mu )}^{2}}}}$ | 偏度计算结果有时候仅反映出外部噪声变化并非生态系统本身状态 Skewness sometimes reflects external noise rather than the ecosystem itself |
| 观察频繁波动 Observing flickering | 计算生态系统状态变量的方差、频率分布的偏度或观察是否出现双峰性 Computing the variance, skewness of frequency distribution of the variables that indicates ecosystem state or observing the bimodality | 适用于出现频繁波动现象的生态系统 Suitable to the ecosystems that flick |
表1 时间维度的生态系统突变早期预警指标
Table 1 Early-warning indicators in ecosystems in temporal dimension
| 主要突变检测方法 Key methods of detecting critical transition | 主要内容 Main contents | 计算公式 Formula | 局限性 Limitation |
|---|---|---|---|
| 测量恢复时间 Measuring the recovery time | 直接测量系统遭受微小事件扰动时恢复到最初平衡态的时间 Directly measuring the recovery time to equilibrium after a small perturbation | 适用于模拟试验, 对现实生态系统可操作性差 Suitable to simulation experiments, but not feasible in reality | |
| 计算自相关系数、方差, 功率谱分析 Computing autocorrelation and variance, and performing power spectrum analysis | 计算指示系统状态的变量的自相关系数、方差, 对时间序列进行功率谱分析 Computing autocorrelation and variance of the variables that indicate the status of the ecosystem, and analyzing the power spectrum of the time series | $\rho =\frac{E[(\mathop{z}_{t}-\mu )(\mathop{z}_{t+1}-\mu )]}{{}^{\mathop{\mathop{s}_{z}}^{2}}}$ | 数据获取困难和数据处理过程带入的误差和主观性 Difficult to acquire data; error and subjectivity are easily brought to the processing |
| $\mathop{s}^{2}=\frac{1}{n}\sum\limits_{t=1}^{n}{\mathop{(\mathop{z}_{t}-\mu )}^{2}}$ | |||
| μ和sz2分别表示状态变量zt的平均值和方差 μ and sz2 represent the average and variance of zt, respectively | |||
| 计算偏度 Computing the skewness | 由一个描述系统状态变量的时间序列数据计算出偏度绝对值 Computing the absolute value of skewness from the time series of variables that indicate ecosystem state | $\mathop{s}_{k}=\frac{\frac{1}{n}\sum\limits_{t=1}^{n}{\mathop{(\mathop{z}_{t}-\mu )}^{3}}}{\sqrt{\frac{1}{n}\sum\limits_{t=1}^{n}{\mathop{(\mathop{z}_{t}-\mu )}^{2}}}}$ | 偏度计算结果有时候仅反映出外部噪声变化并非生态系统本身状态 Skewness sometimes reflects external noise rather than the ecosystem itself |
| 观察频繁波动 Observing flickering | 计算生态系统状态变量的方差、频率分布的偏度或观察是否出现双峰性 Computing the variance, skewness of frequency distribution of the variables that indicates ecosystem state or observing the bimodality | 适用于出现频繁波动现象的生态系统 Suitable to the ecosystems that flick |
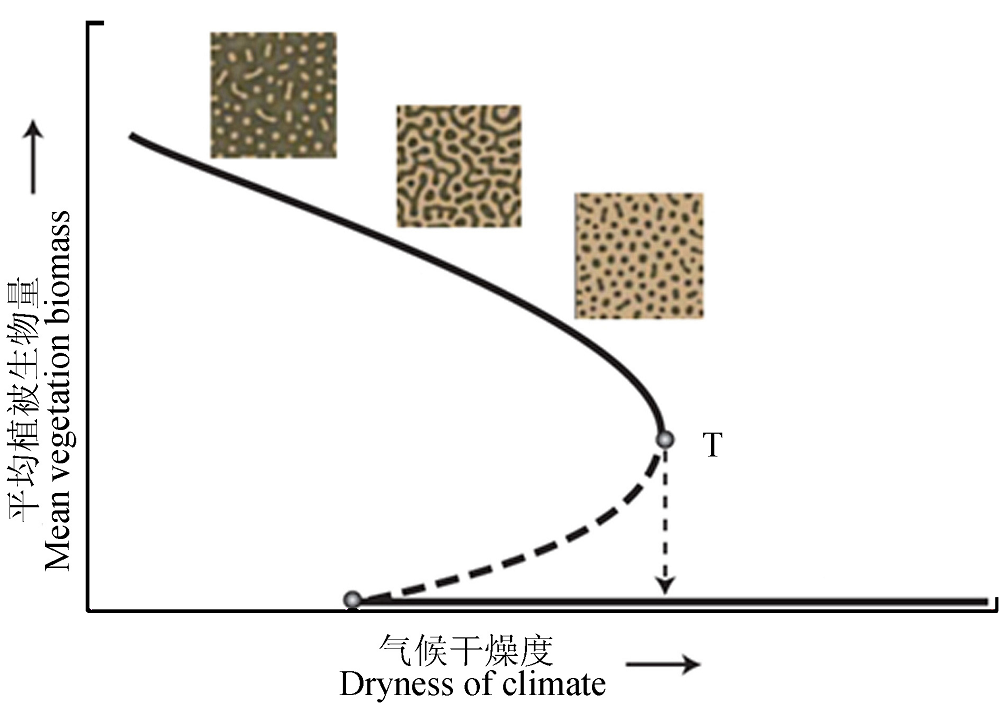
图5 具有自组织规则格局特征的生态系统动态变化。T点, 由规则自组织状态至裸地状态的重大突变。图中实线表示平均均衡态植被密度, 插入的3幅图表示植被斑块: 深色表示植被, 浅色表示裸地。在到达突变点T之前, 斑块由迷宫状向点状变化。(引自Rietkerk et al., 2004)
Fig. 5 Dynamical change of ecosystem with self-organized pattern formation. Point T, critical transition from a self-organized patchy state to a barren state. Solid lines represent mean equilibrium densities of vegetation. The three insets represent vegetation pattern: the dark color represents vegetation and the light color represents bare soil. As the bifurcation point for a critical transition into a barren state is approached, the nature of pattern changes from maze-like to spots. (Cited from Rietkerk et al., 2004)
| 主要突变检测方法 Key methods of detecting critical transition | 主要内容 Main contents | 计算公式 Formula | 局限性 Limitation |
|---|---|---|---|
| 计算空间自相关性和方差 Computing spatial autocorrelation and variance | 计算指示系统状态的变量的空间自相关系数和方差 Computing spatial autocorrelation and variance of the variables that indicate the ecosystem state | 数据获取困难和数据处理过程带入的误差和主观性 Difficult to acquire data; error and subjectivity are easily brought to the processing | |
| 观察power law现象 Observing power law | 分析样地斑块大小S与斑块数目N(S), 观察它们的对数是否满足特定的方程 Analyzing the patch size S and number of patches N(S), and see if their logarithm can meet specific equation | N(S)=CS-γ | 适用地区受限, 计算结果受数据计算方式影响大 Restricted to certain areas and the result is greatly influenced by the computation method |
| 观察规则斑块 Observing regular patches | 观察植被斑块是否呈现规则形状 Observing if the vegetation presents regular patches | 难以对斑块进行量化与判断 Difficult to quantify and judge the patches |
表2 空间维度的生态系统突变早期预警指标
Table 2 Early-warning indicators in ecosystems in spatial dimension
| 主要突变检测方法 Key methods of detecting critical transition | 主要内容 Main contents | 计算公式 Formula | 局限性 Limitation |
|---|---|---|---|
| 计算空间自相关性和方差 Computing spatial autocorrelation and variance | 计算指示系统状态的变量的空间自相关系数和方差 Computing spatial autocorrelation and variance of the variables that indicate the ecosystem state | 数据获取困难和数据处理过程带入的误差和主观性 Difficult to acquire data; error and subjectivity are easily brought to the processing | |
| 观察power law现象 Observing power law | 分析样地斑块大小S与斑块数目N(S), 观察它们的对数是否满足特定的方程 Analyzing the patch size S and number of patches N(S), and see if their logarithm can meet specific equation | N(S)=CS-γ | 适用地区受限, 计算结果受数据计算方式影响大 Restricted to certain areas and the result is greatly influenced by the computation method |
| 观察规则斑块 Observing regular patches | 观察植被斑块是否呈现规则形状 Observing if the vegetation presents regular patches | 难以对斑块进行量化与判断 Difficult to quantify and judge the patches |
| [1] |
Aguiar MR, Sala OE (1999). Patch structure, dynamics and implications for the functioning of arid ecosystems. Trends in Ecology & Evolution, 14, 273-277.
DOI URL PMID |
| [2] |
Berglund N, Gentz B (2002). Metastability in simple climate models: pathwise analysis of slowly driven Langevin equations. Stochastics and Dynamics, 2, 327-356.
DOI URL |
| [3] |
Biggs R, Carpenter SR, Brock WA (2009). Turning back from the brink: detecting an impending regime shift in time to avert it. Proceedings of the National Academy of Sciences of the United States of America, 106, 826-831.
DOI URL PMID |
| [4] |
Bjørnstad ON, Grenfell BT (2001). Noisy clockwork: time series analysis of population fluctuations in animals. Science, 293, 638-643.
URL PMID |
| [5] |
Carpenter SR (2005). Eutrophication of aquatic ecosystems: bistability and soil phosphorus. Proceedings of the National Academy of Sciences of the United States of America, 102, 10002-10005.
URL PMID |
| [6] |
Carpenter SR, Brock WA (2006). Rising variance: a leading indicator of ecological transition. Ecology Letters, 9, 311-318.
URL PMID |
| [7] |
Carpenter SR, Cole JJ, Pace ML, Batt R, Brock WA, Cline T, Coloso J, Hodgson JR, Kitchell JF, Seekell DA (2011). Early warnings of regime shifts: a whole-ecosystem experiment. Science, 332, 1079-1082.
DOI URL PMID |
| [8] |
Carpenter SR, Ludwig D, Brock WA (1999). Management of eutrophication for lakes subject to potentially irreversible change. Ecological Applications, 9, 751-771.
DOI URL |
| [9] |
Dai L, Korolev KS, Gore J (2013). Slower recovery in space before collapse of connected populations. Nature, 496, 355-358.
DOI URL PMID |
| [10] |
Dakos V, Kéfi S, Rietkerk M, van Nes EH, Scheffer M (2011). Slowing down in spatially patterned ecosystems at the brink of collapse. The American Naturalist, 177, E153-E166.
DOI URL PMID |
| [11] |
Dakos V, van Nes EH, Donangelo R, Fort H, Scheffer M (2010). Spatial correlation as leading indicator of catastrophic shifts. Theoretical Ecology, 3, 163-174.
DOI URL |
| [12] |
deMenocal P, Guilderson T, Adkins J, Sarnthein M, Baker L, Yarusinsky M, Ortiz J (2000). Abrupt onset and termination of the African Humid Period: rapid climate responses to gradual insolation forcing. Quaternary Science Reviews, 19, 347-361.
DOI URL |
| [13] |
deYoung B, Barange M, Beaugrand G, Harris R, Perry RI, Scheffer M, Werner F (2008). Regime shifts in marine ecosystems: detection, prediction and management. Trends in Ecology & Evolution, 23, 402-409.
DOI URL PMID |
| [14] |
Donangelo R, Fort H, Dakos V, Scheffer M, van Nes EH (2010). Early warnings for catastrophic shifts in ecosystems: comparison between spatial and temporal indicators. International Journal of Bifurcation and Chaos, 20, 315-321.
DOI URL |
| [15] |
Dunne JA, Williams RJ, Martinez ND (2002). Network structure and biodiversity loss in food webs: robustness increases with connectance. Ecology Letters, 5, 558-567.
DOI URL |
| [16] |
Ellner S, Turchin P (1995). Chaos in a noisy world: new methods and evidence from time-series analysis. The American Naturalist, 145, 343-375.
DOI URL |
| [17] | Feng JF, Wang HL, Zhu L (2009). Review on alternative stable states in ecosystems. Ecology and Environmental Sciences, 18, 1553-1559. (in Chinese with English Abstract) |
| [ 冯剑丰, 王洪礼, 朱琳 (2009). 生态系统多稳态研究进展. 生态环境学报, 18, 1553-1559.] | |
| [18] |
Guttal V, Jayaprakash C (2008). Changing skewness: an early warning signal of regime shifts in ecosystems. Ecology Letters, 11, 450-460.
DOI URL PMID |
| [19] |
Guttal V, Jayaprakash C (2009). Spatial variance and spatial skewness: leading indicators of regime shifts in spatial ecological systems. Theoretical Ecology, 2, 3-12.
DOI URL |
| [20] | Held H, Kleinen T (2004). Detection of climate system bifurcations by degenerate fingerprinting. Geophysical Research Letters, 31, doi: 10.1029/2004GL020972. |
| [21] |
Holling CS (1973). Resilience and stability of ecological systems. Annual Review of Ecology and Systematics, 4, 1-23.
DOI URL |
| [22] | Horsthemke W, Lefever R (1984). Noise-Induced Transitions. Springer, Berlin. |
| [23] |
Isbell F, Tilman D, Polasky S, Binder S, Hawthorne P (2013). Low biodiversity state persists two decades after cessation of nutrient enrichment. Ecology Letters, 16, 454-460.
DOI URL PMID |
| [24] |
Ives AR, Dennis B, Cottingham KL, Carpenter SR (2003). Estimating community stability and ecological interactions from time-series data. Ecological Monographs, 73, 301-330.
DOI URL |
| [25] |
Kéfi S, Rietkerk M, Alados CL, Pueyo Y, Papanastasis VP, ElAich A, de Ruiter PC (2007a). Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature, 449, 213-217.
URL PMID |
| [26] |
Kéfi S, Rietkerk M, van Baalen M, Loreau M (2007b). Local facilitation, bistability and transitions in arid ecosystems. Theoretical Population Biology, 71, 367-379.
URL PMID |
| [27] |
Kleinen T, Held H, Petschel-Held G (2003). The potential role of spectral properties in detecting thresholds in the earth system: application to the thermohaline circulation. Ocean Dynamics, 53, 53-63.
DOI URL |
| [28] |
Kuehn C (2011). A mathematical framework for critical transitions: bifurcations, fast-slow systems and stochastic dynamics. Physica D: Nonlinear Phenomena, 240, 1020-1035.
DOI URL |
| [29] |
Lerdau M (2007). A positive feedback with negative consequences. Science, 316, 212-213.
URL PMID |
| [30] |
Levin SA, Segel LA (1985). Pattern generation in space and aspect. SIAM Review, 27, 45-67.
DOI URL |
| [31] |
Lin Y, Han GD, Zhao ML, Chang SX (2010). Spatial vegetation patterns as early signs of desertification: a case study of a desert steppe in Inner Mongolia, China. Landscape Ecology, 25, 1519-1527.
DOI URL |
| [32] |
Luo YQ, Weng ES (2011). Dynamic disequilibrium of the terrestrial carbon cycle under global change. Trends in Ecology & Evolution, 26, 96-104.
DOI URL PMID |
| [33] |
Maestre FT, Escudero A (2009). Is the patch size distribution of vegetation a suitable indicator of desertification processes? Ecology, 90, 1729-1735.
DOI URL PMID |
| [34] |
Mäler KG (2009). Development, ecological resources and their management: a study of complex dynamic systems. European Economic Review, 44, 645-665.
DOI URL |
| [35] |
Massada AB, Gabay O, Perevolotsky A, Carmel Y (2008). Quantifying the effect of grazing and shrub-clearing on small scale spatial pattern of vegetation. Landscape Ecology, 23, 327-339.
DOI URL |
| [36] |
May RM (1977). Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature, 269, 471-477.
DOI URL |
| [37] | Millennium Ecosystem Assessment (2005). Ecosystem and Human Well-Being: Synthesis. World Resource Institute, Washington, DC. |
| [38] |
Peters DPC, Pielke RA, Bestelmeyer BT, Allen CD, Munson-McGee S, Havstad KM (2004). Cross-scale interactions, nonlinearities, and forecasting catastrophic events. Proceedings of the National Academy of Sciences of the United States of America, 101, 15130-15135.
DOI URL PMID |
| [39] |
Rietkerk M, Dekker SC, de Ruiter PC, van de Koppel J (2004). Self-organized patchiness and catastrophic shifts in ecosystems. Science, 305, 1926-1929.
DOI URL PMID |
| [40] |
Rietkerk M, van de Koppel J (2008). Regular pattern formation in real ecosystems. Trends in Ecology & Evolution, 23, 169-175.
DOI URL PMID |
| [41] | Scheffer M (1990). Multiplicity of stable states in freshwater systems. Hydrobiologia, 61, 475-486. |
| [42] |
Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, Held H, van Nes EH, Rietkerk M, Sugihara G (2009). Early-warning signals for critical transitions. Nature, 461, 53-59.
DOI URL PMID |
| [43] |
Scheffer M, Carpenter SR (2003). Catastrophic regime shifts in ecosystems: linking theory to observation. Trends in Ecology & Evolution, 18, 648-656.
DOI URL |
| [44] |
Scheffer M, Carpenter SR, Foley JA, Folke C, Walker B (2001). Catastrophic shifts in ecosystems. Nature, 413, 591-596.
DOI URL PMID |
| [45] |
Scheffer M, Carpenter SR, Lenton TM, Bascompte J, Brock W, Dakos V, van de Koppel J, van de Leemput IA, Levin SA, van Nes EH (2012). Anticipating critical transitions. Science, 338, 344-348.
URL PMID |
| [46] |
Scheffer M, Hosper SH, Meijer ML, Moss B, Jeppesen E (1993). Alternative equilibria in shallow lakes. Trends in Ecology & Evolution, 8, 275-279.
DOI URL PMID |
| [47] |
Stachowicz JJ (2001). Mutualism, facilitation, and the structure of ecological communities: positive interactions play a critical, but underappreciated, role in ecological communities by reducing physical or biotic stresses in existing habitats and by creating new habitats on which many species depend. BioScience, 51, 235-246.
DOI URL |
| [48] |
Staver AC, Archibald S, Levin SA (2011). The global extent and determinants of savanna and forest as alternative biome states. Science, 334, 230-232.
DOI URL PMID |
| [49] |
Steneck RS, Vavrinec J, Leland AV (2004). Accelerating trophic-level dysfunction in kelp forest ecosystems of the western North Atlantic. Ecosystems, 7, 323-332.
DOI URL |
| [50] | Synergy Program for Analyzing Resilience and Critical Transitions (2012). Early Warning Signals Toolbox. http://www.early-warning-signals.org/?page_id=480. Cited 18 July 2013. |
| [51] |
van Nes EH, Rip WJ, Scheffer M (2007). A theory for cyclic shifts between alternative states in shallow lakes. Ecosystems, 10, 17-28.
DOI URL |
| [52] |
van Nes EH, Scheffer M (2005). Implications of spatial heterogeneity for catastrophic regime shifts in ecosystems. Ecology, 86, 1797-1807.
DOI URL |
| [53] |
van Nes EH, Scheffer M (2007). Slow recovery from perturbations as a generic indicator of a nearby catastrophic shift. The American Naturalist, 169, 738-747.
DOI URL PMID |
| [54] |
Veraart AJ, Faassen EJ, Dakos V, van Nes EH, Lürling M, Scheffer M (2011). Recovery rates reflect distance to a tipping point in a living system. Nature, 481, 357-359.
URL PMID |
| [55] |
von Hardenberg J, Meron E, Shachak M, Zarmi Y (2001). Diversity of vegetation patterns and desertification. Physical Review Letters, 87, 198101.
DOI URL PMID |
| [56] |
Wang R, Dearing JA, Langdon PG, Zhang EL, Yang XD, Dakos V, Scheffer M (2012). Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature, 492, 419-422.
DOI URL PMID |
| [57] |
Wissel C (1984). A universal law of the characteristic return time near thresholds. Oecologia, 65, 101-107.
DOI URL PMID |
| [58] |
Wu JG (2013). Landscape sustainability science: ecosystem services and human well-being in changing landscapes. Landscape Ecology, 28, 999-1023.
DOI URL |
| [59] | Yu L, Hao BL (1984). Phase Transitions and Critical Phenomena. Science Press, Beijing. (in Chinese) |
| [ 于渌, 郝柏林 (1984). 相变和临界现象. 科学出版社, 北京.] |
| [1] | 韩路, 冯宇, 李沅楷, 王雨晴, 王海珍. 地下水埋深对灰胡杨叶片与土壤养分生态化学计量特征及其内稳态的影响[J]. 植物生态学报, 2024, 48(1): 92-102. |
| [2] | 李安艳, 黄先飞, 田源斌, 董继兴, 郑菲菲, 夏品华. 贵州草海草-藻型稳态转换过程中叶绿素a的变化及其影响因子[J]. 植物生态学报, 2023, 47(8): 1171-1181. |
| [3] | 贺强. 生物互作与全球变化下的生态系统动态: 从理论到应用[J]. 植物生态学报, 2021, 45(10): 1075-1093. |
| [4] | 陈婵, 张仕吉, 李雷达, 刘兆丹, 陈金磊, 辜翔, 王留芳, 方晰. 中亚热带植被恢复阶段植物叶片、凋落物、土壤碳氮磷化学计量特征[J]. 植物生态学报, 2019, 43(8): 658-671. |
| [5] | 刘璐, 葛结林, 舒化伟, 赵常明, 徐文婷, 申国珍, 谢宗强. 神农架常绿落叶阔叶混交林碳氮磷化学计量比[J]. 植物生态学报, 2019, 43(6): 482-489. |
| [6] | 唐海萍, 陈姣, 薛海丽. 生态阈值: 概念、方法与研究展望[J]. 植物生态学报, 2015, 39(9): 932-940. |
| [7] | 刘超, 王洋, 王楠, 王根轩. 陆地生态系统植被氮磷化学计量研究进展[J]. 植物生态学报, 2012, 36(11): 1205-1216. |
| [8] | 温学发, 张世春, 孙晓敏, 于贵瑞. 叶片水H218O富集的研究进展[J]. 植物生态学报, 2008, 32(4): 961-966. |
| [9] | 王炜, 刘钟龄, 郝敦元, 梁存柱. 内蒙古草原退化群落恢复演替的研究II. 恢复演替时间进程的分析[J]. 植物生态学报, 1996, 20(5): 460-471. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
Copyright © 2022 版权所有 《植物生态学报》编辑部
地址: 北京香山南辛村20号, 邮编: 100093
Tel.: 010-62836134, 62836138; Fax: 010-82599431; E-mail: apes@ibcas.ac.cn, cjpe@ibcas.ac.cn
备案号: 京ICP备16067583号-19